इयत्ता 8 वी विस्तार सूत्रे म्हणजे काय? : विस्तार सूत्रे म्हणजे बहुपदीय समीकरणे किंवा गृहितांकांच्या स्वरूपात दिलेल्या संकल्पनांचे विस्तारित स्वरूप. उदाहरणार्थ, (a+b)^2=a^2+2ab+b^2 हे एक विस्तार सूत्र आहे. अशा सूत्रांच्या मदतीने संक्षिप्त बैजिक राशी अधिक व्यापक स्वरूपात व्यक्त करता येतात.

विस्तार सूत्रे म्हणजे काय?
विस्तार सूत्रे ही गणितातील महत्त्वाची संकल्पना असून ती बहुपदींच्या विस्तारासाठी आणि सरलीकरणासाठी वापरली जातात. विस्तार सूत्रे बीजगणित आणि संख्याशास्त्रात महत्त्वाची भूमिका बजावतात. संगणकीय गणितीय मॉडेलिंगसाठी आणि अल्गोरिदमच्या अचूकतेसाठी देखील विस्तार सूत्रे उपयोगी पडतात.
मूलभूत विस्तार सूत्रे
- (x+y)^2 = x^{2} + 2xy + y^{2}
- (x-y)^2 = x^2 - 2xy + y^2
- (x+y)(x-y) = x^2 - xy + xy - y^2 = x^2 - y^2
मित्रांनो, ह्या वरून विस्तार सूत्रे म्हणजे काय, हे तुमच्या लक्षात आलं असेल. ही विस्तार सूत्रे आणि आपण पुढे जी शिकणार आहोत ती सगळी विस्तार सूत्रे पक्की लक्षात ठेवण्यासाठी तुम्ही ह्या विस्तार सूत्रांचा एक तक्ता तयार करून तुमच्या घरात भिंतीवर लावून ठेवा आणि जाता येता त्यावर नजर टाका, जेणे करून ही विस्तार सूत्रे तुमच्या कायम लक्षात राहतील.
आता पुढील सगळी उदाहरणं सोडवताना पहिलं काय करायचं; तर दिलेलं उदाहरण नीट शांतपणे वाचायचं. उदाहरण नीट वाचलं की तुमच्या चटकन लक्षात येईल की हे उदाहरण सोडवायला कोणतं विस्तार सूत्र वापरायचं आहे. विस्तार सूत्रे वापरून जी उदाहरणं आपण सोडवणार आहोत, ती सोडवताना तुमच्या लक्षात येईल की ही उदाहरण म्हणजे केवळ बेरीज, वजाबाकी, गुणाकार, भागाकार ह्या मूलभूत गणिती क्रिया आहेत. ह्याच्यात महत्वाचं फक्त हे आहे की ह्या मूलभूत गणिती क्रिया काळजीपूर्वक गोंधळून न जाता करायच्या.
चला तर मग आता आपण ह्या विस्तारसुत्रांची काही उदाहरणं सोडवून बघूया,
उदाहरण 1:
(x+2y)^2
उत्तर:
वरील विस्तार सूत्र 1 वापरून,
(x+2y)^2 = x^2 + 4xy + 4y^2
उदाहरण 2:
(2x-5y)^2
उत्तर:
वरील विस्तार सूत्र 2 वापरून,
\begin{aligned}(2x-5y)^2 &= (2x)^2 - 2(10xy) + (5y)^2 \\ &= 4x^2 - 20xy + 25y^2\end{aligned}
उदाहरण 3:
(101)^2
उत्तर:
वरील विस्तार सूत्र 1 वापरून,
\begin{aligned} \\ (101)^2 &= (100+1)^2\\ &=(100)^2+2(100\times 1)+1^2 \\ &=10000+200+1 \\ &=10201\end{aligned}
उदाहरण 4:
(98)^2
उत्तर:
वरील विस्तार सूत्र 2 वापरून,
\begin{aligned} \\ (98)^2 &= (100-2)^2 \\ &=(100)^2-2(100\times 2)+(2)^2\\&=10000-400+4\\&=9604\end{aligned}
उदाहरण 5:
(5m+3n)(5m-3n)
उत्तर:
वरील विस्तार सूत्र 3 वापरून,
\begin{aligned} \\ (5m+3n)(5m-3n) &= (5m)^2-(3n)^2 \\ &=25m^2-9n^2\end{aligned}
आयत आणि चौरस यांच्या क्षेत्रफळांच्या सूत्रांच्या साहाय्याने \mathbf{(x+a)(x+b)} चा विस्तार …
चौरसाचे आणि आयताचे क्षेत्रफळ काढायचे सूत्र हे एकच आहे.
चौरसाचे / आयताचे क्षेत्रफळ = लांबी x रुंदी
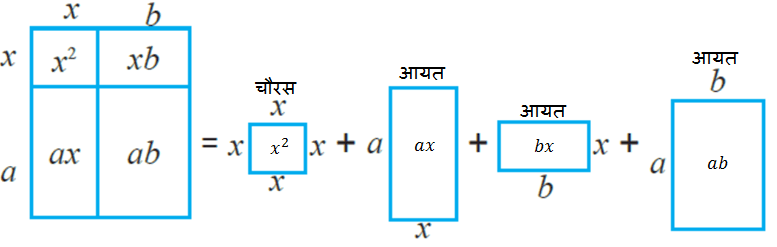
पण इथे एक लक्षात घ्या की चौरसाच्या चारही बाजू ह्या समान असतात आणि त्यामुळे लांबी आणि रुंदी समान असते.
\thereforeचौरसाचे क्षेत्रफळ = (चौरसाची कोणतीही बाजू)2
\therefore (x+a)(x+b)=x^2+ ax+bx+ab
\therefore (x+a)(x+b)=x^2+ x(a+b)+ ab
| महत्वाचं: \mathbf{(x+a)} आणि \mathbf{(x+b)} यांना एक पद समान असलेल्या द्विपदी म्हणतात. \mathbf{(x+a)(x+b)=x^2+ x(a+b)+ab} |
विस्तार सूत्रांची उदाहरणे
उदाहरण 1:
(x+3)(x+5)
उत्तर:
(x+3) आणि (x+5) ह्या एक पद समान असलेल्या द्विपदी असल्याने (x+a)(x+b)=x^2+ x(a+b)+ab हे विस्तार सूत्र वापरून हे उदाहरण सोडवावं लागेल.
\begin{aligned} \\ \therefore (x+3)(x+5)&=x^2+5x+3x+(3\times 5) \\ &= x^2+x(5+3)+(15) \\ &= x^2+8x+15\end{aligned}
उदाहरण 2:
(x+7)(x-2)
उत्तर:
(x+7) आणि (x-2) ह्या एक पद समान असलेल्या द्विपदी असल्याने (x+a)(x-b)=x^2+ x(a+b)+ab हे विस्तार सूत्र वापरून हे उदाहरण सोडवावं लागेल.
\begin{aligned} \\ \therefore (x+7)(x-2)&= x^2-2x+7x+(7\times (-2)) \\ &= x^2+x(-2+7)+(-14) \\ &=x^2+5x-14\end{aligned}
उदाहरण 3:
(2a+3b)(2a-3b)
उत्तर:
(2a+3b) आणि (2a-3b) ह्या एक पद समान असलेल्या द्विपदी असल्याने (x+a)(x+b)=x^2+ x(a+b)+ab हे विस्तार सूत्र वापरून हे उदाहरण सोडवावं लागेल.
\begin{aligned} \\ \therefore (2a+3b)(2a-3b)&=(2a)^2-(2a\times3b)+(3b\times2a)-(3b\times3b) \\ &= 4a^2+(-3b+3b)2a-9b^2 \\ &= 4a^2+(0)2a-9b^2 \\ &= 4a^2-9b^2\end{aligned}
उदाहरण 4:
\left(m+\frac{3}{2}\right)\left(m+\frac{1}{2}\right)
उत्तर:
\left(m+\frac{3}{2}\right) आणि \left(m+\frac{1}{2}\right) ह्या एक पद समान असलेल्या द्विपदी असल्याने (x+a)(x+b)=x^2+ x(a+b)+ab हे विस्तार सूत्र वापरून हे उदाहरण सोडवावं लागेल.
\begin{aligned} \\ \therefore \left(m+\frac{3}{2}\right)\left(m+\frac{1}{2}\right)&=m^2+\left(\frac{3}{2}+\frac{1}{2}\right)m+\left(\frac{3}{2}\times \frac{1}{2}\right) \\ &=m^2+\left(\frac{4}{2}\right)m+\left(\frac{3}{4}\right) \\ &=m^2+2m+\frac{3}{4}\end{aligned}
उदाहरण 5:
\left(x-7\right)\left(x-2\right)
उत्तर:
\left(x-7\right) आणि \left(x-2\right) ह्या एक पद समान असलेल्या द्विपदी असल्याने (x+a)(x+b)=x^2+ x(a+b)+ab हे विस्तार सूत्र वापरून हे उदाहरण सोडवावं लागेल.
\begin{aligned} \\ \therefore \left(x-7\right)\left(x-2\right)&= x^2+\left(-2x-7x\right)+\left(-7\times -2\right) \\ &= x^2+\left(-2-7\right)x+14 \\ &= x^2-9x+14\end{aligned}
उदाहरण 6:
\left(a+2\right)\left(a-1\right)
उत्तर:
\left(a+2\right) आणि \left(a-1\right) ह्या एक पद समान असलेल्या द्विपदी असल्याने (x+a)(x+b)=x^2+ x(a+b)+ab हे विस्तार सूत्र वापरून हे उदाहरण सोडवावं लागेल.
\begin{aligned} \\ \therefore \left(a+2\right)\left(a-1\right)&=a^2+\left(-a+2a\right)+\left(2\times -1\right) \\ &=a^2+a-2\end{aligned}
उदाहरण 7:
\left(m-4\right)\left(m+6\right)
उत्तर:
\left(m-4\right) आणि \left(m+6\right) ह्या एक पद समान असलेल्या द्विपदी असल्याने (x+a)(x+b)=x^2+ x(a+b)+ab हे विस्तार सूत्र वापरून हे उदाहरण सोडवावं लागेल.
\begin{aligned} \\ \therefore \left(m-4\right)\left(m+6\right)&=m^2+\left(6m-4m\right)+\left(-4\times 6\right) \\ &=m^2+2m-24\end{aligned}
उदाहरण 8:
\left(p+8\right)\left(p-3\right)
उत्तर:
\left(p+8\right) आणि \left(p-3\right) ह्या एक पद समान असलेल्या द्विपदी असल्याने (x+a)(x+b)=x^2+ x(a+b)+ab हे विस्तार सूत्र वापरून हे उदाहरण सोडवावं लागेल.
\begin{aligned} \\ \therefore\left(p+8\right)\left(p-3\right)&=p^2+\left(-3p+8p\right)+\left(8\times -3\right) \\ &=p^2+5p-24\end{aligned}
उदाहरण 9:
\left(a+2\right)\left(a-1\right)
उत्तर:
\left(a+2\right) आणि \left(a-1\right) ह्या एक पद समान असलेल्या द्विपदी असल्याने (x+a)(x+b)=x^2+ x(a+b)+ab हे विस्तार सूत्र वापरून हे उदाहरण सोडवावं लागेल.
\begin{aligned} \\ \therefore \left(a+2\right)\left(a-1\right)&=a^2-a+2a-2 \\ &=a^2+a-2\end{aligned}
उदाहरण 10:
\left(p+8\right)\left(p-3\right)
उत्तर:
\left(p+8\right) आणि \left(p-3\right) ह्या एक पद समान असलेल्या द्विपदी असल्याने (x+a)(x+b)=x^2+ x(a+b)+ab हे विस्तार सूत्र वापरून हे उदाहरण सोडवावं लागेल.
\begin{aligned} \\ \therefore \left(p+8\right)\left(p-3\right)&=p^2-3p+8p-24 \\ &=p^2+5p-24\end{aligned}
उदाहरण 11:
\left(m-4\right)\left(m+6\right)
उत्तर:
\left(m-4\right) आणि \left(m+6\right) ह्या एक पद समान असलेल्या द्विपदी असल्याने (x+a)(x+b)=x^2+ x(a+b)+ab हे विस्तार सूत्र वापरून हे उदाहरण सोडवावं लागेल.
\begin{aligned} \\ \therefore \left(m-4\right)\left(m+6\right)&=m^2+6m-4m-24 \\ &=m^2+2m-24\end{aligned}
उदाहरण 12:
\left(13+x\right)\left(13-x\right)
उत्तर:
\left(13+x\right) आणि \left(13-x\right) ह्या एक पद समान असलेल्या द्विपदी असल्याने (x+a)(x+b)=x^2+ x(a+b)+ab हे विस्तार सूत्र वापरून हे उदाहरण सोडवावं लागेल.
\begin{aligned} \\ \therefore \left(13+x\right)\left(13-x\right)&=13^2-13x+13x-x^2 \\ &=169-x^2\end{aligned}
उदाहरण 13:
\left(3x+4y\right)\left(3x+5y\right)
उत्तर:
\left(3x+4y\right) आणि \left(3x+5y\right) ह्या एक पद समान असलेल्या द्विपदी असल्याने (x+a)(x+b)=x^2+ x(a+b)+ab हे विस्तार सूत्र वापरून हे उदाहरण सोडवावं लागेल.
\begin{aligned} \\ \therefore \left(3x+4y\right)\left(3x+5y\right)&=\left(3x\times 3x\right)+\left(3x\times 5y\right)+\left(4y\times 3x\right)+\left(4y\times 5y\right) \\ &=9x^2+15xy+12xy+20y^2 \\ &=9x^2+27xy+20y^2\end{aligned}
उदाहरण 14:
\left(9x-5t\right)\left(9x+3t\right)
उत्तर:
\left(9x-5t\right) आणि \left(9x+3t\right) ह्या एक पद समान असलेल्या द्विपदी असल्याने (x+a)(x+b)=x^2+ x(a+b)+ab हे विस्तार सूत्र वापरून हे उदाहरण सोडवावं लागेल.
\begin{aligned} \\ \therefore \left(3x+4y\right)\left(3x+5y\right)&=\left(3x\times3x\right)+\left(3x\times5y\right)+\left(4y\times3x\right)+\left(4y\times5y\right) \\ &=9x^2+15xy+12xy+20y^2 \\ &=9x^2+27xy+20y^2\end{aligned}
उदाहरण 15:
\left(m+\frac{2}{3}\right)\left(m-\frac{7}{3}\right)
उत्तर:
\left(m+\frac{2}{3}\right) आणि \left(m-\frac{7}{3}\right) ह्या एक पद समान असलेल्या द्विपदी असल्याने (x+a)(x+b)=x^2+ x(a+b)+ab हे विस्तार सूत्र वापरून हे उदाहरण सोडवावं लागेल.
\begin{aligned} \\ \therefore \left(m+\frac{2}{3}\right)\left(m-\frac{7}{3}\right)&=\left(m\times m\right)+\left(-\frac{7}{3} m\right)+\left(\frac{2}{3} m\right)+\left(\frac{2}{3}\times -\frac{7}{3}\right) \\ &=m^2+\left(-\frac{7}{3}+\frac{2}{3}\right)m-\frac{14}{9} \\ &=m^2-\frac{5}{3} m-\frac{14}{9}\end{aligned}
उदाहरण 16:
\left(x+\frac{1}{x}\right)\left(x-\frac{1}{x}\right)
उत्तर:
\left(x+\frac{1}{x}\right) आणि \left(x-\frac{1}{x}\right) ह्या एक पद समान असलेल्या द्विपदी असल्याने (x+a)(x+b)=x^2+ x(a+b)+ab हे विस्तार सूत्र वापरून हे उदाहरण सोडवावं लागेल.
\begin{aligned} \\ \therefore \left(x+\frac{1}{x}\right)\left(x-\frac{1}{x}\right)&=\left(x\times x\right)+\left(-\frac{x}{x}\right)+\left(\frac{x}{x}\right)+\left(\frac{1}{x}\times -\frac{1}{x}\right) \\ &=x^2-1+1- \frac{1}{x^2} \\ &=x^2-\frac{1}{x^2}\end{aligned}
उदाहरण 17:
\left(\frac{1}{y}+4\right)\left(\frac{1}{y}-9\right)
उत्तर:
\left(\frac{1}{y}+4\right) आणि \left(\frac{1}{y}-9\right) ह्या एक पद समान असलेल्या द्विपदी असल्याने (x+a)(x+b)=x^2+ x(a+b)+ab हे विस्तार सूत्र वापरून हे उदाहरण सोडवावं लागेल.
\begin{aligned} \\ \therefore \left(\frac{1}{y}+4\right)\left(\frac{1}{y}-9\right)&=\left(\frac{1}{y}\times \frac{1}{y}\right)+\left(\frac{1}{y}\times -9\right)+\left(4\times \frac{1}{y}\right)+\left(4\times -9\right) \\ &=\left(\frac{1}{y^2} \right)-\frac{9}{y}+\frac{4}{y}-36 \\ &=\frac{1}{y^2}-\frac{5}{y}-36\end{aligned}
\mathbf{\left(a+b\right)^3} चा विस्तार
\begin{aligned}\left(a+b\right)^3&=\left(a+b\right)\left(a+b\right)^2\\&=\left(a+b\right)\left(a^2+2ab+b^2\right)\\&=a\left(a^2+2ab+b^2 \right)+b\left(a^2+2ab+b^2\right)\\&=a^3+2a^2 b+ab^2+a^2 b+2ab^2+b^3\\&=a^3+3a^2 b+3ab^2+b^3\end{aligned}
| \mathbf{\therefore \left(a+b\right)^3=a^3+3a^2 b+3ab^2+b^3} |
\left(a+b\right)^3 चं हे विस्तार सूत्र पक्क लक्षात ठेवायचं. चला तर मग आता आपण हे विस्तार सूत्र वापरून काही उदाहरणं सोडवूयात.
उदाहरण 1:
\begin{aligned} \\ \left(x+3\right)^3&=\left(x+3\right)\left(x+3\right)^2 \\ &=\left(x+3\right)\left(x^2+6x+9\right) \\ &=x\left(x^2+6x+9\right)+3\left(x^2+6x+9\right) \\ &=x^3+6x^2+9x+3x^2+18x+27 \\ &=x^3+9x^2+27x+27\end{aligned}
उदाहरण 2:
\begin{aligned} \\ \left(3x+4y\right)^3&=\left(3x+4y\right)\left(3x+4y\right)^2 \\ &=\left(3x+4y\right)\left(9x^2+24xy+16y^2\right) \\ &=3x\left(9x^2+24xy+16y^2 \right)+4y\left(9x^2+24xy+16y^2\right) \\ &=27x^3+72x^2 y+48xy^2+36x^2 y+96xy^2+64y^3 \\ &=27x^3+108x^2 y+144xy^2+64y^3\end{aligned}
उदाहरण 3:
\begin{aligned} \\ \left(\frac{2m}{n}+\frac{n}{2m}\right)^3&=\frac{8m^3}{n^3}+3\left(\frac{4m^2n}{2n^2m}\right)+3\left(\frac{2mn^2}{4m^2n}\right)+\left(\frac{n^3}{8m^3}\right) \\ &=\frac{8m^3}{n^3}+3\left(\frac{4m^2n}{2n^2m}\right)+3\left(\frac{2mn^2}{4m^2n}\right)+\left(\frac{n^3}{8m^3}\right) \\ &=\frac{8m^3}{n^3}+3\left(\frac{2m}{n}\right)+3\left(\frac{n}{2m}\right)+\left(\frac{n^3}{8m^3}\right) \\ &=\frac{8m^3}{n^3}+\frac{6m}{n}+\frac{3n}{2m}+\frac{n^3}{8m^3}\end{aligned}
उदाहरण 4:
\begin{aligned} \\ \left(41\right)^3&=\left(40+1\right)^3\\&=40^3+3\left(40^2\times 1\right)+3\left(40\times 1^2\right)+1^3 \\ &=64000+4800+120+1\\&=68921\end{aligned}
आता आपण \mathbf{\left(a+b\right)^3=a^3+3a^2b+3ab^2+b^3} हे विस्तार सूत्र वापरून अजून काही उदाहरणं सोडवूयात,
उदाहरण 1:
\left(k+4\right)^3
उत्तर:
इथे a=k,b=4
\begin{aligned} \\ \therefore \left(k+4\right)^3&=k^3+3\left(k^24\right)+3\left(k4^2\right)+4^3 \\ &=k^3+12k^2+48k+64\end{aligned}
उदाहरण 2:
\left(7x+8y\right)^3
उत्तर:
इथे a=7x,y=8y
\begin{aligned}\therefore \left(7x+8y\right)^3&=\left(7x\right)^3+[3\times \left(7x\right)^2\times 8y]+[3\times 7x\times \left(8y\right)^2]+\left(8y\right)^3 \\ &=343x^3+1176x^2y+1344xy^2+512y^3\end{aligned}
उदाहरण 3:
\left(7+m\right)^3
उत्तर:
इथे a=7,b=m
\begin{aligned} \\ \therefore \left(7+m\right)^3&=7^3+3\left(7^2\times m\right)+3\left(7\times m^2\right)+m^3 \\ &=343+147m+21m^2+m^3\end{aligned}
उदाहरण 4:
\left(52\right)^3=\left(50+2\right)^3
उत्तर:
इथे a=50,b=2
\begin{aligned} \\ \therefore \left(50+2\right)^3&=50^3+3\left(50^2\times2\right)+3\left(50\times2^2\right)+2^3 \\ &=125000+15000+600+8 \\ &=140608\end{aligned}
उदाहरण 5:
\left(101\right)^3=\left(100+1\right)^3
उत्तर:
इथे a=100,b=1
\begin{aligned} \\ \therefore \left(100+1\right)^3&=100^3+3\left(100^2\times1\right)+3\left(100\times1^2\right)+1^3 \\ &=1000000+30000+300+1 \\ &=1030301\end{aligned}
उदाहरण 6:
\left(x+\frac{1}{x}\right)^3
उत्तर:
इथे a=x,b=\frac{1}{x}
\begin{aligned} \\ \therefore \left(x+\frac{1}{x}\right)^3&=x^3+3\left(\frac{x^2}{x}\right)+3\left(\frac{x}{x^2}\right)+\left(\frac{1}{x}\right)^3 \\ &=x^3+3x+\frac{3}{x}+\frac{1}{x^3}\end{aligned}
उदाहरण 7:
\left(2m+\frac{1}{5}\right)^3
उत्तर:
इथे a=2m,b=\frac{1}{5}
\begin{aligned} \\ \therefore \left(2m+\frac{1}{5}\right)^3&=8m^3+3\left(\frac{4m^2}{5}\right)+3\left(\frac{2m}{5^2}\right)+\left(\frac{1}{5}\right)^3 \\ &=8m^3+\left(\frac{12m^2}{5}\right)+\left(\frac{6m}{25}\right)+\left(\frac{1}{125}\right) \\ &=8m^3+\frac{12m^2}{5}+\frac{6m}{25}+\frac{1}{125}\end{aligned}
उदाहरण 8:
\left(\frac{5x}{y}+\frac{y}{5x}\right)^3
उत्तर:
इथे a=\frac{5x}{y},b=\frac{y}{5x}
\begin{aligned}\therefore \left(\frac{5x}{y}+\frac{y}{5x}\right)^3&=\left(\frac{5x}{y}\right)^3+3\left(\frac{25x^2}{y^2}\times \frac{y}{5x}\right)+3\left(\frac{5x}{y}\times \frac{y^2}{25x^2}\right)+\left(\frac{y}{5x}\right)^3 \\ &=\left(\frac{5x}{y}\right)^3+3\left(\frac{5x}{y}\right)+3\left(\frac{y}{5x}\right)+\left(\frac{y}{5x}\right)^3 \\ &=\frac{125x^3}{y^3}+\frac{15x}{y}+\frac{3y}{5x}+\frac{y^3}{125x^3}\end{aligned}
\mathbf{\left(a-b\right)^3} चा विस्तार
\begin{aligned}\left(a-b\right)^3&=\left(a-b\right)\left(a-b\right)^2 \\ &=\left(a-b\right)\left(a-b\right)^2 \\ &=\left(a-b\right)\left(a^2-2ab+b^2\right) \\ &=a\left(a^2-2ab+b^2\right)-b\left(a^2-2ab+b^2\right) \\ &=a^3-2a^2b+ab^2-a^2b+2ab^2-b^3 \\ &=a^3-3a^2b+3ab^2-b^3\end{aligned}
| \begin{aligned}\mathbf{\left(a-b\right)^3=a^3-3a^2b+3ab^2-b^3}\end{aligned} |
\left(a-b\right)^3 चं हे विस्तार सूत्र पक्क लक्षात ठेवायचं. चला तर मग आता आपण हे विस्तार सूत्र वापरून काही उदाहरणं सोडवूयात.
उदाहरण 1:
\left(x-2\right)^3
उत्तर:
इथे a=x,b=2
\begin{aligned} \\ \left(x-2\right)^3&=x^3-3\left(x^2\times 2\right)+3\left(x\times 2^2\right)-2^3 \\ &=x^3-6x^2+12x-8\end{aligned}
उदाहरण 2:
\left(4p-5q\right)^3
उत्तर:
इथे a=4p,b=5q
\begin{aligned} \\ \left(4p-5q\right)^3&=\left(4p\right)^3-3\left(\left(4p\right)^2\times 5q\right)+3\left(4p\times \left(5q\right)^2\right)-\left(5q\right)^3 \\ &=64p^3-240p^2q+300pq^2-125q^3\end{aligned}
उदाहरण 3:
\left(99\right)^3=\left(100-1\right)^3
उत्तर:
इथे a=100,b=1
\begin{aligned} \\ \left(100-1\right)^3&=100^3-3\left(100^2\times 1\right)+3\left(100\times 1^2\right)-1^3 \\ &=1000000-30000+300-1 \\ &=970299\end{aligned}
उदाहरण 4:
\left(p+q\right)^3+\left(p-q\right)^3
उत्तर:
इथे a=p,b=q
इथे हे लक्षात घ्या की \left(p+q\right)^3 हे \left(a+b\right)^3 चं विस्तार सूत्र वापरून आणि \left(p-q\right)^3 हे \left(a-b\right)^3 हे चं विस्तार सूत्र वापरून सोडवावं लागेल
\begin{aligned} \\ \therefore \left(p+q\right)^3+\left(p-q\right)^3=&[p^3+3p^2q+3pq^2+q^3]+ \\ &[p^3-3p^2q+3pq^2-q^3] \\ =&\;p^3+\cancel{3p^2q}+3pq^2+\cancel{q^3}+ \\ &\;p^3-\cancel{3p^2q}+3pq^2-\cancel{q^3} \\ =&\;2p^3+6pq^2\end{aligned}
उदाहरण 5:
\left(2x+3y\right)^3-\left(2x-3y\right)^3
उत्तर:
इथे a=2x,b=3y
इथे हे लक्षात घ्या की \left(2x+3y\right)^3 हे \left(a+b\right)^3 चं विस्तार सूत्र वापरून आणि \left(2x-3y\right)^3 हे \left(a-b\right)^3 हे चं विस्तार सूत्र वापरून सोडवावं लागेल.
\begin{aligned} \\ \left(2x+3y\right)^3-\left(2x-3y\right)^3=& \;\left(2x\right)^3+3\left(\left(2x\right)^2\times3y\right)+3\left(2x\times\left(3y\right)^2\right)+\left(3y\right)^3]- \\ & \;[\left(2x\right)^3-3\left(2x\right)^2\times3y+3\left(2x\times\left(3y\right)^2\right)-\left(3y\right)^3] \\ =& \;[8x^3+36x^2y+54xy^2+27y^3]-\\ & \;[8x^3-36x^2y+54xy^2-27x^3] \\ =& \;\cancel{8x^3}+36x^2y+\cancel{54xy^2}+27y^3- \\ & \;\cancel{8x^3}+36x^2y-\cancel{54xy^2}+27x^3 \\ =& \;72x^2y+54x^3\end{aligned}
आता आपण \left(a-b\right)^3=a^3-3a^2b+3ab^2-b^3 हे विस्तार सूत्र वापरून अजून काही उदाहरणं सोडवूयात,
उदाहरण 1:
\left(2m-5\right)^3
उत्तर:
इथे a=2m,b=5
\begin{aligned} \\ \left(2m-5\right)^3&=\left(2m\right)^3-3\left(\left(2m\right)^2\times 5\right)+3\left(2m\times 5^2\right)-\left(5\right)^3 \\ &=8m^3-3\left(20m^2\right)+3\left(50m\right)-\left(125\right) \\ &=8m^3-60m^2+150m-125\end{aligned}
उदाहरण 2:
\left(4-p\right)^3
उत्तर:
इथे a=4,b=p
\begin{aligned} \\ \left(4-p\right)^3&=\left(4\right)^3-3\left(4^2\times p\right)+3\left(4\times p^2\right)-\left(p\right)^3 \\ &=64-48p+12p^2-p^3\end{aligned}
उदाहरण 3:
\left(7x-9y\right)^3
उत्तर:
इथे a=7x,b=9y
\begin{aligned} \\ \left(7x-9y\right)^3=\left(7x\right)^3-3\left(\left(7x\right)^2\times9y\right)+3\left(7x\times\left(9y\right)^2\right)-\left(9y\right)^3 \\ &=343x^3-1323x^2y+1701xy^2-729y^3\end{aligned}
उदाहरण 4:
\left(58\right)^3=\left(60-2\right)^3
उत्तर:
इथे a=60,b=2
\begin{aligned} \\ \left(60-2\right)^3&=\left(60\right)^3-3\left(\left(60\right)^2\times2\right)+3\left(60\times\left(2\right)^2\right)-\left(2\right)^3 \\ &=216000-21600+720-8 \\ &=195112\end{aligned}
उदाहरण 5:
\left(198\right)^3=\left(200-2\right)^3
उत्तर:
इथे a=200,b=2
\begin{aligned} \\ \left(200-2\right)^3&=\left(200\right)^3-3\left(\left(200\right)^2\times2\right)+3\left(200\times\left(2\right)^2\right)-\left(2\right)^3 \\ &=8000000-240000+2400-8 \\ &=7762392\end{aligned}
उदाहरण 6:
\left(2p-\frac{1}{2p}\right)^3
उत्तर:
इथे a=2p,b=\frac{1}{2p}
\begin{aligned} \\ \left(2p-\frac{1}{2p}\right)^3&=\left(2p\right)^3-3\left[\left(2p\right)^2\times\frac{1}{2p}\right]+3\left[2p\times\left(\frac{1}{2p}\right)^2\right]-\left(\frac{1}{2p}\right)^3 \\ &=8p^3-6p+\frac{3}{2p}-\frac{1}{8p^3}\end{aligned}
उदाहरण 7:
\left(1-\frac{1}{a}\right)^3
उत्तर:
इथे a=1,b=\frac{1}{a}
\begin{aligned} \\ \left(1-\frac{1}{a}\right)^3&=\left(1\right)^3-3\left[\left(1\right)^2\times\frac{1}{a}\right]+3\left[1\times\left(\frac{1}{a}\right)^2\right]-\left(\frac{1}{a}\right)^3 \\ &=1-\frac{3}{a}+\frac{3}{a^2}-\frac{1}{a^3}\end{aligned}
उदाहरण 8:
\left(\frac{x}{3}-\frac{3}{x}\right)^3
उत्तर:
इथे a=\frac{x}{3},b=\frac{3}{x}
\begin{aligned} \\ \left(\frac{x}{3}-\frac{3}{x}\right)^3&=\left(\frac{x}{3}\right)^3-3\left[\left(\frac{x}{3}\right)^2\times \frac{3}{x}\right]+3\left[\frac{x}{3}\times \left(\frac{3}{x}\right)^2\right]-\left(\frac{3}{x}\right)^3 \\ &=\frac{x^3}{27}-3\left(\frac{3x^2}{9x}\right)+3\left(\frac{9x}{3x^2}\right)-\frac{27}{x^3} \\ &=\frac{x^3}{27}-\left(\frac{9x^2}{9x}\right)+\left(\frac{27x}{3x^2}\right)-\frac{27}{x^3} \\ &=\frac{x^3}{27}-x+\frac{9}{x}-\frac{27}{x^3}\end{aligned}
\mathbf{\left(a+b\right)^3} आणि \mathbf{\left(a-b\right)^3} ची उदाहरणं
खाली दिलेली \left(a+b\right)^3 आणि \left(a-b\right)^3 ह्या दोन्हींची अगदी सोपी पण महत्वाची विस्तार सूत्र पक्की लक्षात ठेवायची आणि मुख्य म्हणजे गणित सोडवताना ह्या दोन्ही विस्तार सूत्रांतील धन (+) आणि ऋण (-) चिन्हांचा गोंधळ होऊ द्यायचा नाही. दिलेलं गणित नीट वाचा आणि ते \left(a+b\right)^3 ह्या स्वरूपात आहे की \left(a-b\right)^3 ह्या स्वरूपात आहे, हे लक्षात घेऊन त्याप्रमाणे विस्तार सूत्राची निवड करा. \left(a+b\right)^3 च्या सूत्रात सगळीकडे धन (+) चिन्ह आहे तर \left(a-b\right)^3 च्या सूत्रात पहिले व तिसरे ऋण (-) चिन्ह आहे, हे लक्षात ठेवा.
- \mathbf{\left(a+b\right)^3=a^3+3a^2b+3ab^2+b^3}
- \mathbf{\left(a-b\right)^3=a^3-3a^2b+3ab^2-b^3}
चला तर मग आता ही दोन्ही विस्तार सूत्र वापरून अजून काही उदाहरणं सोडवूयात. इथे लक्षात घ्या की आपल्याला \left(a+b\right)^3 आणि \left(a-b\right)^3 दोन्हींची विस्तार सूत्र वापरावी लागणार आहेत.
उदाहरण 1:
\left(2a+b\right)^3-\left(2a-b\right)^3
उत्तर:
आधी आपण हे दोन कंस वेगवेगळे सोडवून घेऊ,
\begin{aligned} \\ \therefore\left(2a+b\right)^3=&\left(2a\right)^3+3\left(\left(2a\right)^2\times b\right)+ \\ &\;3\left(2a\times \left(b\right)^2\right)+\left(b\right)^3 \\ =&\;8a^3+3\left(4a^2b\right)+3\left(2ab^2\right)+b^3\end{aligned}
\begin{aligned} \\ \therefore\left(2a-b\right)^3=&\left(2a\right)^3-3\left(\left(2a\right)^2\times b\right)+ \\ &\;3\left(2a\times \left(b\right)^2\right)-\left(b\right)^3 \\ =&\;8a^3-3\left(4a^2b\right)+3\left(2ab^2\right)-b^3\end{aligned}
\begin{aligned} \\ \therefore\left(2a+b\right)^3-\left(2a-b\right)^3=&\;\cancel{8a^3}+12a^2b+\cancel{6ab^2}+b^3- \\ &\;\cancel{8a^3}+12a^2b-\cancel{6ab^2}+b^3 \\ =&\;24a^2b+2b^3\end{aligned}
उदाहरण 2:
\left(3r-2k\right)^3+\left(3r+2k\right)^3
उत्तर:
आधी आपण हे दोन कंस वेगवेगळे सोडवून घेऊ,
\begin{aligned} \\ \therefore\left(3r-2k\right)^3=&\left(3r\right)^3-3\left(\left(3r\right)^2\times2k\right)+ \\ &\;3\left(3r\times\left(2k\right)^2\right)-\left(2k\right)^3 \\ =&\;27r^3-3\left(18r^2k\right)+3\left(12rk^2\right)-8k^3\end{aligned}
\begin{aligned} \\ \therefore\left(3r+2k\right)^3=&\left(3r\right)^3+3\left(\left(3r\right)^2\times2k\right)+ \\ &\;3\left(3r\times\left(2k\right)^2\right)+\left(2k\right)^3 \\ =&\;27r^3+3\left(18r^2k\right)+3\left(12rk^2\right)+8k^3\end{aligned}
\begin{aligned} \\ \left(3r-2k\right)^3+\left(3r+2k\right)^3=&\;27r^3-\cancel{54r^2k}+36rk^2-\cancel{8k^3}+ \\ &\;27r^3+\cancel{54r^2k}+36rk^2+\cancel{8k^3} \\ =&\;54r^3+72rk^2\end{aligned}
उदाहरण 3:
\left(4a-3\right)^3-\left(4a+3\right)^3
उत्तर:
आधी आपण हे दोन कंस वेगवेगळे सोडवून घेऊ,
\begin{aligned} \\ \therefore\left(4a-3\right)^3=&\left(4a\right)^3-3\left(\left(4a\right)^2\times 3\right)+ \\ &\;3\left(4a\times \left(3\right)^2\right)-\left(3\right)^3 \\ =&\;64a^3-144a^2+108a-27\end{aligned}
\begin{aligned} \\ \therefore\left(4a+3\right)^3=&\left(4a\right)^3+3\left(\left(4a\right)^2\times 3\right)+ \\ &\;3\left(4a\times \left(3\right)^2\right)+\left(3\right)^3 \\ =&\;64a^3-144a^2-108a-27\end{aligned}
\begin{aligned} \\ \left(4a-3\right)^3-\left(4a+3\right)^3=&\;\cancel{64a^3}-144a^2+\cancel{108a}-27- \\ &\;\cancel{64a^3}-144a^2-\cancel{108a}-27 \\ =&\;-288a^2-54\end{aligned}
उदाहरण 4:
\left(5x-7y\right)^3+\left(5x+7y\right)^3
उत्तर:
आधी आपण हे दोन कंस वेगवेगळे सोडवून घेऊ,
\begin{aligned} \\ \therefore\left(5x-7y\right)^3=&\left(5x\right)^3-3\left(\left(5x\right)^2\times 7y\right)+ \\ &\;3\left(5x\times \left(7y\right)^2\right)-\left(7y\right)^3 \\ =&\;125x^3-525x^2y+735xy^2-343y^3\end{aligned}
\begin{aligned} \\ \therefore\left(5x+7y\right)^3=&\left(5x\right)^3+3\left(\left(5x\right)^2\times 7y\right)+ \\ &\;3\left(5x\times \left(7y\right)^2\right)+\left(7y\right)^3 \\ =&\;125x^3+525x^2y+735xy^2+343y^3\end{aligned}
\begin{aligned} \\ \therefore\left(5x-7y\right)^3+\left(5x+7y\right)^3=&\;125x^3-\cancel{525x^2y}+735xy^2-\cancel{343y^3}+ \\ &\;125x^3+\cancel{525x^2y}+735xy^2+\cancel{343y^3} \\ =&\;250x^3+1470xy^2\end{aligned}
\mathbf{\left(a+b+c\right)^2} चा विस्तार
\begin{aligned} \\ \left(a+b+c\right)^2&=\left(a+b+c\right)\times \left(a+b+c\right) \\ &=a\left(a+b+c\right)+b\left(a+b+c\right)+c\left(a+b+c\right) \\ &=a^2+ab+ac+ab+b^2+bc+ac+bc+c^2 \\ &=a^2+b^2+c^2+2ab+2bc+2ac\end{aligned}
| \mathbf{\left(a+b+c\right)^2=a^2+b^2+c^2+2ab+2bc+2ac} |
चला तर मग आता आपण ह्याचं विस्तार सूत्र वापरून काही उदाहरणं सोडवूयात,
उदाहरण 1:
\left(x+y+3\right)^2
उत्तर:
\begin{aligned} \\ \therefore \left(x+y+3\right)^2&=x^2+y^2+9+2xy+6y+6x \\ &=x^2+y^2+6x+6y+2xy+9\end{aligned}
उदाहरण 2:
\left(2p+3q+4r\right)^2
उत्तर:
\begin{aligned} \\ \therefore \left(2p+3q+4r\right)^2=&\left(2p\right)^2+\left(3q\right)^2+\left(4r\right)^2+ \\ &\;2\left(2p\times 3q\right)+2\left(3q\times 4r\right)+2\left(2p\times 4r\right) \\ =&\;4p^2+9q^2+16r^2+12pq+24qr+16pr\end{aligned}
उदाहरण 3:
\left(a+2b+c\right)^2+\left(a-2b+c\right)^2
उत्तर:
आधी आपण हे दोन कंस वेगवेगळे सोडवून घेऊ,
\begin{aligned} \\ \therefore\left(a+2b+c\right)^2=&\left(a\right)^2+\left(2b\right)^2+\left(c\right)^2+ \\ &\;2\left(a\times 2b\right)+2\left(2b\times c\right)+2\left(a\times c\right) \\ =&\;a^2+4b^2+c^2+4ab+4bc+2ac\end{aligned}
\begin{aligned} \\ \therefore\left(a-2b+c\right)^2=&\left(a\right)^2+\left(2b\right)^2+\left(c\right)^2- \\ &\;2\left(a\times 2b\right)-2\left(2b\times c\right)+2\left(a\times c\right) \\ =&\;a^2+4b^2+c^2-4ab-4bc+2ac\end{aligned}
\begin{aligned} \\ \therefore\left(a+2b+c\right)^2+\left(a-2b+c\right)^2=&\;a^2+4b^2+c^2+\cancel{4ab}+\cancel{4bc}+2ac+ \\ &\;a^2+4b^2+c^2-\cancel{4ab}-\cancel{4bc}+2ac \\ =&\;2a^2+8b^2+2c^2+4ac\end{aligned}
उदाहरण 4:
\left(2m+n+5\right)^2
उत्तर:
\begin{aligned} \\ \therefore \left(2m+n+5\right)^2=&\left(2m\right)^2+\left(n\right)^2+\left(5\right)^2+2\left(2m\times n\right)+ \\ &\;2\left(n\times 5\right)+2\left(2m\times 5\right) \\ =&\;4m^2+n^2+25+4mn+10n+20m\end{aligned}
उदाहरण 5:
\left(p+2q+3r\right)^2
उत्तर:
\begin{aligned} \\ \therefore \left(p+2q+3r\right)^2=&\left(p\right)^2+\left(2q\right)^2+\left(3r\right)^2+2\left(p\times 2q\right)+ \\ &\;2\left(2q\times 3r\right)+2\left(p\times 3r\right) \\ =&\;p^2+4q^2+9r^2+4pq+12qr+6pr\end{aligned}
उदाहरण 6:
\left(3a+4b-5k\right)^2
उत्तर:
\begin{aligned} \\ \therefore \left(3a+4b-5k\right)^2=&\left(3a\right)^2+\left(4b\right)^2+\left(-5k\right)^2+2\left(3a\times 4b\right)+ \\ &\;2\left(4b\times \left(-5k\right)\right)+2\left(3a\times \left(-5k\right)\right) \\ =&\;9a^2+16b^2+25k^2+24ab-40bk-30ak\end{aligned}
उदाहरण 7:
\left(7p-3q-4r\right)^2
उत्तर:
\begin{aligned} \\ \therefore \left(7p-3q-4r\right)^2=&\left(7p\right)^2+\left(-3q\right)^2+\left(-4r\right)^2+2\left(7p\times \left(-3q\right)\right)+ \\ &\;2\left(\left(-3q\right)\times \left(-4r\right)\right)+2\left(7p\times \left(-4r\right)\right) \\ =&\;49p^2+9q^2+16r^2-42pq+24qr-56pr\end{aligned}
उदाहरण 8:
\left(a-2b+3\right)^2+\left(a+2b-3\right)^2
उत्तर:
आधी आपण हे दोन कंस वेगवेगळे सोडवून घेऊ,
\begin{aligned} \\ \therefore\left(a-2b+3\right)^2=&\left(a\right)^2+\left(-2b\right)^2+\left(3\right)^2+2\left(a\times \left(-2b\right)\right)+ \\ &\;2\left(\left(-2b\right)\times 3\right)+2\left(a\times 3\right) \\ =&\;a^2+4b^2+9-4ab-12b+6a\end{aligned}
\begin{aligned} \\ \therefore\left(a+2b-3\right)^2=&\left(a\right)^2+\left(2b\right)^2+\left(-3\right)^2+2\left(a\times \left(2b\right)\right)+ \\ &\;2\left(\left(2b\right)\times \left(-3\right)\right)+2\left(a\times \left(-3\right)\right) \\ =&\;a^2+4b^2+9+4ab-12b-6a\end{aligned}
\begin{aligned} \\ \therefore\left(a-2b+3\right)^2+\left(a+2b-3\right)^2=&\;a^2+4b^2+9-\cancel{4ab}-12b+\cancel{6a}+ \\ &\;a^2+4b^2+9+\cancel{4ab}-12b-\cancel{6a} \\ =&\;2a^2+8b^2+18-24b\end{aligned}
उदाहरण 9:
\left(3x-4y-2z\right)^2-\left(3x+4y-2z\right)^2
उत्तर:
आधी आपण हे दोन कंस वेगवेगळे सोडवून घेऊ,
\begin{aligned} \\ \therefore\left(3x-4y-2z\right)^2=&\left(3x\right)^2+\left(-4y\right)^2+\left(-2z\right)^2+2\left(\left(3x\right)\times \left(-4y\right)\right)+ \\ &\;2\left(\left(-4y\right)\times \left(-2z\right)\right)+2\left(\left(3x\right)\times \left(-2z\right)\right) \\ =&\;9x^2+16y^2+4z^2-24xy+16yz-12xz\end{aligned}
\begin{aligned} \\ \therefore\left(3x+4y-2z\right)^2=&\left(3x\right)^2+\left(4y\right)^2+\left(-2z\right)^2+2\left(\left(3x\right)\times \left(4y\right)\right)+ \\ &\;2\left(\left(4y\right)\times \left(-2z\right)\right)+2\left(\left(3x\right)\times \left(-2z\right)\right) \\ =&\;9x^2+16y^2+4z^2+24xy-16yz-12xz\end{aligned}
\begin{aligned} \\ \therefore\left(3x-4y-2z\right)^2-\left(3x+4y-2z\right)^2=\;&\cancel{9x^2}+\cancel{16y^2}+\cancel{4z^2}-24xy+16yz-\cancel{12xz}- \\ &\cancel{9x^2}-\cancel{16y^2}-\cancel{4z^2}-24xy+16yz+\cancel{12xz} \\ =&\;32yz-48xy\end{aligned}
उदाहरण 10:
\left(7p-6q+5r\right)^2+\left(7p+6q-5r\right)^2
उत्तर:
आधी आपण हे दोन कंस वेगवेगळे सोडवून घेऊ,
\begin{aligned} \\ \therefore\left(7p-6q+5r\right)^2=&\left(7p\right)^2+\left(-6q\right)^2+\left(5r\right)^2+2\left(\left(7p\right)\times \left(-6q\right)\right)+ \\ &\;2\left(\left(-6q\right)\times \left(5r\right)\right)+2\left(\left(7p\right)\times \left(5r\right)\right) \\ =&\;49p^2+36q^2+25r^2-84pq-60qr+70pr\end{aligned}
\begin{aligned} \\ \therefore\left(7p+6q-5r\right)^2=&\left(7p\right)^2+\left(6q\right)^2+\left(-5r\right)^2+2\left(\left(7p\right)\times \left(6q\right)\right)+ \\ &\;2\left(\left(6q\right)\times \left(-5r\right)\right)+2\left(\left(7p\right)\times \left(-5r\right)\right) \\ =&\;49p^2+36q^2+25r^2+84pq-60qr-70pr\end{aligned}
\begin{aligned} \\ \therefore\left(7p-6q+5r\right)^2+\left(7p+6q-5r\right)^2=&\;49p^2+36q^2+25r^2-\cancel{84pq}-60qr+\cancel{70pr}+ \\ &\;49p^2+36q^2+25r^2+\cancel{84pq}-60qr-\cancel{70pr} \\ =&\;98p^2+72q^2+50r^2-120qr\end{aligned}
| थोडक्यात: गणितातील विस्तार सूत्रे ही संकल्पना बहुपदींच्या सरलीकरणासाठी उपयुक्त ठरते. भौतिकशास्त्र, अभियांत्रिकी आणि संगणकीय गणितात विस्तार सूत्रे वापरून जटिल समीकरणे सोपी केली जातात. ग्राफिक्स आणि सिग्नल प्रोसेसिंगमध्येही विस्तार सूत्रे मोठ्या प्रमाणावर वापरली जातात. मूलभूत विस्तार सूत्रे: (x+y)^2 = x^{2} + 2xy + y^{2} (x-y)^2 = x^2 - 2xy + y^2 (x+y)(x-y) = x^2 - xy + xy - y^2 = x^2 - y^2 विस्तार सूत्रे वापरून आपण खालील बैजिक राशींचा विस्तार कसा करायचा ते पहिलं, \mathbf{\left(a+b\right)^3} \mathbf{\left(a-b\right)^3} \mathbf{\left(a+b+c\right)^2} |
इयत्ता 8 वीचे पाठयपुस्तक: इथे क्लिक करा
