इयत्ता 8 वी वर्तुळाची जीवा व कंस म्हणजे काय? : वर्तुळाची जीवा व कंस यांचा उपयोग गणित, अभियांत्रिकी, वास्तुकला, आणि भौतिकशास्त्र यामध्ये मोठ्या प्रमाणात होतो. जीवा व कंस वर्तुळाच्या रचनेतील महत्त्वाचे घटक आहेत आणि त्यांचे गुणधर्म विविध गणितीय संकल्पनांसाठी उपयुक्त ठरतात.

वर्तुळाची जीवा म्हणजे काय?
वर्तुळाची जीवा व कंस ह्या संकल्पना समजावून घेताना आपण आधी वर्तुळाची जीवा म्हणजे काय ते पाहू,
वर्तुळाच्या परिघावरील दोन बिंदूंना जोडणाऱ्या रेषाखंडाला त्या वर्तुळाची “जीवा” असं म्हणतात.
| (1) वर्तुळाचे केंद्र व त्या वर्तुळातील जीवेचा मध्यबिंदू जोडणारा रेषाखंड हा त्या जीवेला लंब असतो. (2) वर्तुळाच्या केंद्रातून जीवेवर टाकलेला लंब जीवेला दुभागतो; म्हणजे जीवेची दोन समान लांबीच्या रेषाखंडात विभागणी करतो. |

वरील आकृतीत रेख AB ही वर्तुळाची जीवा आहे, बिंदू O हा वर्तुळाचं केंद्र आहे आणि रेख OP हा वर्तुळाच्या केंद्रातून जीवेवर टाकलेला लंब आहे.
(1) \therefore m\angle APO=m\angle BPO=90^\circ.
(2) लंब OP हा जीवा AB ला दुभागतो \therefore \ell\left(AP\right)=\ell\left(BP\right).
वर्तुळाच्या जीवा उदाहरणे
वर्तुळाची जीवा व कंस ह्या संकल्पना समजावून घेण्यासाठी आपण वर्तुळाच्या जीवेची काही उदाहरणं पाहू,
उदा 1:
जीवा AB=7 सेमी. रेख OP\parallel जीवा AB, तर रेख AP ची लांबी काढा.
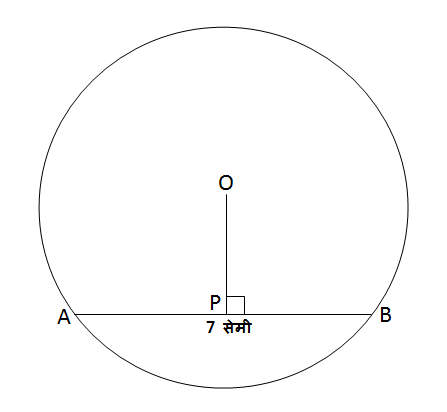
उत्तर:
आपल्याला माहित आहे की वर्तुळाच्या केंद्रातून जीवेवर टाकलेला लंब जीवेला दुभागतो; म्हणजे जीवेची दोन समान लांबीच्या रेषाखंडात विभागणी करतो.
\therefore \ell\left(AP\right)=\ell\left(BP\right) आणि \ell\left(AP\right)+\ell\left(BP\right)=\ell\left(AB\right)
\begin{aligned} \\ &\therefore \ell\left(AP\right)+\ell\left(BP\right)=7 \\ &\therefore 2\times \ell\left(AP\right)=7 \\ &\therefore \frac{2}{2}\times \ell\left(AP\right)=\frac{7}{2} \\ &\therefore \ell\left(AP\right)=3.5\end{aligned}
रेख \mathbf{AP} ची लांबी 3.5 सेमी आहे.
उदा 2:
केंद्र O असलेल्या एका वर्तुळाची त्रिज्या 10 सेमी आहे. त्या वर्तुळाची एक जीवा केंद्रापासून 6 सेमी अंतरावर आहे, तर त्या जीवेची लांबी काढा.
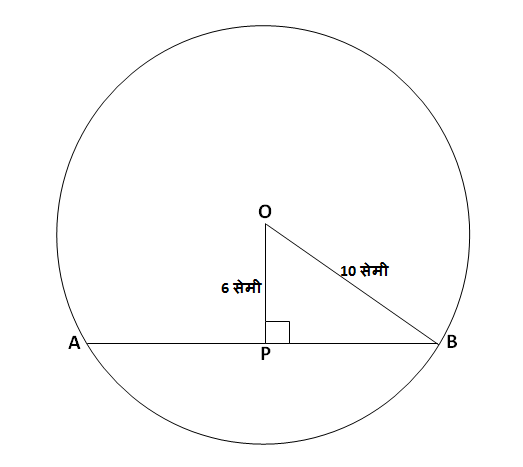
उत्तर:
वरील आकृतीत दाखवल्याप्रमाणे वर्तुळाची त्रिज्या, जीवा आणि जीवेचं वर्तुळाच्या केंद्रापासूनचं अंतर, हे मिळून \triangle OPB हा काटकोन त्रिकोण तयार झालेला आहे.
आपल्याला माहित आहे की वर्तुळाच्या केंद्रातून जीवेवर टाकलेला लंब जीवेला दुभागतो; म्हणजे जीवेची दोन समान लांबीच्या रेषाखंडात विभागणी करतो.
\therefore \ell\left(AP\right)=\ell\left(BP\right) आणि \therefore जीवा \ell\left(AB\right)=\ell\left(AP\right)+\ell\left(BP\right)=2\times \ell\left(BP\right)
त्यामुळे आपल्याला आधी रेख BP ची लांबी काढून घ्यावी लागणार आहे. \triangle OPB हा काटकोन त्रिकोण असल्याने आपण पायथॅगोरसच्या सूत्राने रेख BP ची लांबी काढून घेऊ,
पायथॅगोरसच्या सूत्राप्रमाणे,
\begin{aligned} \\ &\therefore \ell\left(OB\right)^2=\ell\left(OP\right)^2+\ell\left(BP\right)^2 \\ &\therefore \left(10\right)^2=\left(6\right)^2+\ell\left(BP\right)^2 \\ &\therefore 100=36+\ell\left(BP\right)^2 \\ &\therefore \ell\left(BP\right)^2=100-36 \\ &\therefore \ell\left(BP\right)^2=64 \\ &\therefore \sqrt{\ell\left(BP\right)^2}=\sqrt{64} \\ &\therefore \ell\left(BP\right)=8\end{aligned}
रेख \mathbf{BP} ची लांबी 8 सेमी आहे.
\begin{aligned} \\ &\therefore \ell\left(AB\right)=2\times \ell\left(BP\right) \\ &\therefore \ell\left(AB\right)=2\times 8 \\ &\therefore \ell\left(AB\right)=16\end{aligned}
\mathbf{\therefore } जीवा \mathbf{AB} ची लांबी 16 सेमी आहे.
उदा 3:
केंद्र O असलेल्या वर्तुळाच्या जीवा AB ची लांबी 13 सेमी आहे. रेख OP जीवा AB, तर \ell\left(PB\right).

उत्तर:
आपल्याला माहित आहे की वर्तुळाच्या केंद्रातून जीवेवर टाकलेला लंब जीवेला दुभागतो; म्हणजे जीवेची दोन समान लांबीच्या रेषाखंडात विभागणी करतो.
\therefore \ell\left(AP\right)=\ell\left(BP\right) आणि \ell\left(AP\right)+\ell\left(BP\right)=\ell\left(AB\right)
\begin{aligned} \\ &\therefore \ell\left(AP\right)+\ell\left(BP\right)=13 \\ &\therefore 2\times \ell\left(AP\right)=13 \\ &\therefore \frac{2}{2}\times \ell\left(AP\right)=\frac{13}{2} \\ &\therefore \ell\left(AP\right)=6.5\end{aligned}
रेख \mathbf{AP} ची लांबी 6.5 सेमी आहे.
उदा 4:
केंद्र O असलेल्या वर्तुळाची त्रिज्या 25 सेमी आहे. या वर्तुळात 48 सेमी लांबीची एक जीवा काढली, तर वर्तुळ केंद्रापासून तीकिती अंतरावर असेल ?
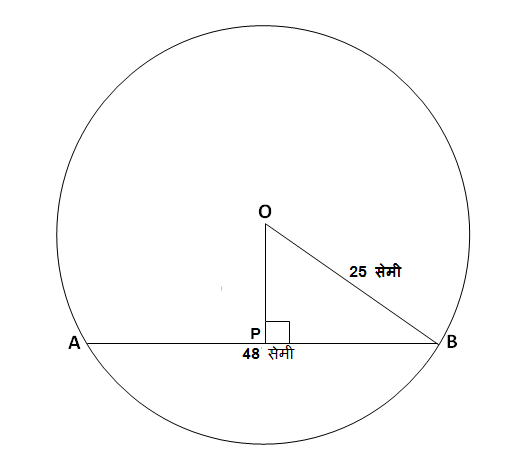
उत्तर:
वरील आकृतीत दाखवल्याप्रमाणे वर्तुळाची त्रिज्या, जीवा आणि जीवेचं वर्तुळाच्या केंद्रापासूनचं अंतर, हे मिळून \triangle OPB हा काटकोन त्रिकोण तयार झालेला आहे.
आपल्याला माहित आहे की वर्तुळाच्या केंद्रातून जीवेवर टाकलेला लंब जीवेला दुभागतो; म्हणजे जीवेची दोन समान लांबीच्या रेषाखंडात विभागणी करतो.
\therefore \ell\left(AP\right)=\ell\left(BP\right) आणि जीवा \ell\left(AB\right)=\ell\left(AP\right)+\ell\left(BP\right)=2\times \ell\left(BP\right)
\begin{aligned} \\ &\therefore 2\times \ell\left(BP\right)=\ell\left(AB\right) \\ &\therefore 2\times \ell\left(BP\right)=48 \\ &\therefore \ell\left(BP\right)=\frac{1}{2}\times 48 \\ &\therefore \ell\left(BP\right)=24\end{aligned}
\triangle OPB हा काटकोन त्रिकोण असल्याने आपण पायथॅगोरसच्या सूत्राने आता रेख OP ची लांबी काढू,
पायथॅगोरसच्या सूत्राप्रमाणे,
\begin{aligned} \\ &\therefore \ell\left(OB\right)^2=\ell\left(OP\right)^2+\ell\left(BP\right)^2 \\ &\therefore \left(25\right)^2=\ell\left(OP\right)^2+\left(24\right)^2 \\ &\therefore 625=576+\ell\left(OP\right)^2 \\ &\therefore \ell\left(OP\right)^2=625-576 \\ &\therefore \ell\left(OP\right)^2=49 \\ &\therefore \sqrt{\ell\left(OP\right)^2}=\sqrt{49} \\ &\therefore \ell\left(OP\right)=7\end{aligned}
\mathbf{\therefore }जीवा \mathbf{AB} वर्तुळ केंद्र \mathbf{O} पासून 7 सेमी अंतरावर आहे.
उदा 5:
O केंद्र असलेल्या वर्तुळाची एक जीवा 24 सेमी लांबीची असून ती वर्तुळ केंद्रापासून 9 सेमी अंतरावर आहे, तर त्या वर्तुळाची त्रिज्या काढा.

उत्तर:
वरील आकृतीत दाखवल्याप्रमाणे वर्तुळाची त्रिज्या, जीवा आणि जीवेचं वर्तुळाच्या केंद्रापासूनचं अंतर, हे मिळून \triangle OPB हा काटकोन त्रिकोण तयार झालेला आहे.
आपल्याला माहित आहे की वर्तुळाच्या केंद्रातून जीवेवर टाकलेला लंब जीवेला दुभागतो; म्हणजे जीवेची दोन समान लांबीच्या रेषाखंडात विभागणी करतो.
\therefore \ell\left(AP\right)=\ell\left(BP\right) आणि जीवा \ell\left(AB\right)=\ell\left(AP\right)+\ell\left(BP\right)=2\times \ell\left(BP\right)
\begin{aligned} \\ &\therefore 2\times \ell\left(BP\right)=\ell\left(AB\right) \\ &\therefore 2\times \ell\left(BP\right)=24 \\ &\therefore \ell\left(BP\right)=\frac{1}{2}\times 24 \\ &\therefore \ell\left(BP\right)=12\end{aligned}
\triangle OPB हा काटकोन त्रिकोण असल्याने आपण पायथॅगोरसच्या सूत्राने आता त्रिज्या OB ची लांबी काढूया,
पायथॅगोरसच्या सूत्राप्रमाणे,
\begin{aligned} \\ &\therefore \ell\left(OB\right)^2=\ell\left(OP\right)^2+\ell\left(BP\right)^2 \\ &\therefore \ell\left(OB\right)^2=\left(9\right)^2+\left(12\right)^2 \\ &\therefore \ell\left(OB\right)^2=81+144 \\ &\therefore \ell\left(OB\right)^2=225 \\ &\therefore \sqrt{\ell\left(OB\right)^2}=\sqrt{225} \\ &\therefore \ell\left(OB\right)=15\end{aligned}
\mathbf{\therefore } वर्तुळाची त्रिज्या 15 सेमी आहे.
उदा 6:
एका वर्तुळाचे केंद्र C असून त्याची त्रिज्या 10 सेमी आहे. त्या वर्तुळाच्या एका जीवेची लांबी 12 सेमी असेल तर ती जीवा केंद्रापासून किती अंतरावर असेल?

उत्तर:
वरील आकृतीत दाखवल्याप्रमाणे वर्तुळाची त्रिज्या, जीवा आणि जीवेचं वर्तुळाच्या केंद्रापासूनचं अंतर, हे मिळून \triangle CPB हा काटकोन त्रिकोण तयार झालेला आहे.
आपल्याला माहित आहे की वर्तुळाच्या केंद्रातून जीवेवर टाकलेला लंब जीवेला दुभागतो; म्हणजे जीवेची दोन समान लांबीच्या रेषाखंडात विभागणी करतो.
\therefore \ell\left(AP\right)=\ell\left(BP\right) आणि जीवा \ell\left(AB\right)=\ell\left(AP\right)+\ell\left(BP\right)=2\times \ell\left(BP\right)
\begin{aligned} \\ &\therefore 2\times \ell\left(BP\right)=\ell\left(AB\right) \\ &\therefore 2\times \ell\left(BP\right)=12 \\ &\therefore \ell\left(BP\right)=\frac{1}{2}\times 12 \\ &\therefore \ell\left(BP\right)=6\end{aligned}
\triangle CPB हा काटकोन त्रिकोण असल्याने आपण पायथॅगोरसच्या सूत्राने आता रेख CP ची लांबी काढू,
पायथॅगोरसच्या सूत्राप्रमाणे,
\begin{aligned} \\ &\therefore \ell\left(CB\right)^2=\ell\left(CP\right)^2+\ell\left(BP\right)^2 \\ &\therefore \left(10\right)^2=\ell\left(CP\right)^2+\left(6\right)^2 \\ &\therefore 100=36+\ell\left(CP\right)^2 \\ &\therefore \ell\left(CP\right)^2=100-36 \\ &\therefore \ell\left(CP\right)^2=64 \\ &\therefore \sqrt{\ell\left(CP\right)^2}=\sqrt{64} \\ &\therefore \ell\left(CP\right)=8\end{aligned}
\mathbf{\therefore }जीवा \mathbf{AB} वर्तुळ केंद्र \mathbf{C} पासून 8 सेमी अंतरावर आहे.
वर्तुळाचा कंस म्हणजे काय?
वर्तुळाची जीवा व कंस ह्या संकल्पना समजावून घेताना आपण आधी वर्तुळाचा कंस म्हणजे काय ते पाहू,
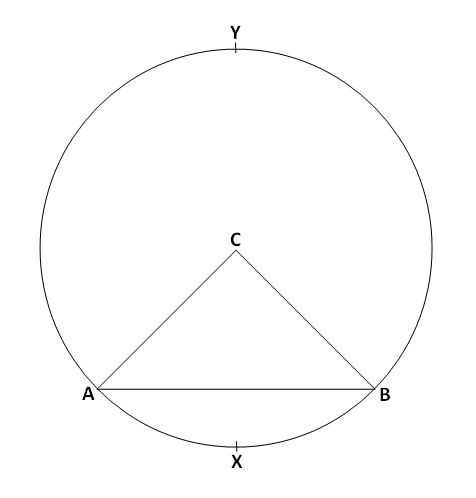
वरील आकृतीत केंद्र C असलेले वर्तुळ दिलेले आहे. रेख AB ही ह्या वर्तुळाची जीवा आहे.
वर्तुळाचा कंस:
ह्या वर्तुळाच्या परिघावरून आपण बिंदू A पासून बिंदू B पर्यंत गेलो तर जो मार्ग मिळतो, त्याला “वर्तुळाचा कंस” असं म्हणतात. म्हणजेच कंस हा वर्तुळाच्या परिघाचा एक भाग असतो. वरील आकृतीत AYB हा वर्तुळाच्या परिघाचा एक भाग आहे, जो “कंस AYB” असा दर्शवतात. त्याच प्रमाणे AXB हा देखील वर्तुळाच्या परिघाचा एक भाग असून तो “कंस AXB” असा दर्शवतात.
लघु कंस आणि विशाल कंस:
कंस AXB ला समाविष्ट करणारा \angle ACB हा लघुकोन (90^\circ पेक्षा लहान कोन) असल्याने कंस AXB ला वर्तुळाचा “लघु कंस” असं म्हणतात. \angle ACB सोडून राहिलेला कोन हा विशालकोन असल्याने \left[\left(360^\circ-m\angle ACB\right)>90^\circ\right] कंस AYB ला वर्तुळाचा “विशाल कंस” म्हणतात.
संगत कंस आणि संगत जीवा:
रेख AB हा वर्तुळाची जीवा आहे. कंस AXB आणि कंस AYB ह्यांना जीवा AB चे “संगत कंस” म्हणतात. आणि जीवा AB ला कंस AXB आणि कंस AYB ची “संगत जीवा” म्हणतात.
कंसाची आणि जीवांची एकरूपता:
वर्तुळाची जीवा व कंस ह्या संकल्पना समजावून घेताना आपण जीवा व कंस यांच्या एकरूपतेविषयी जाणून घेऊ,
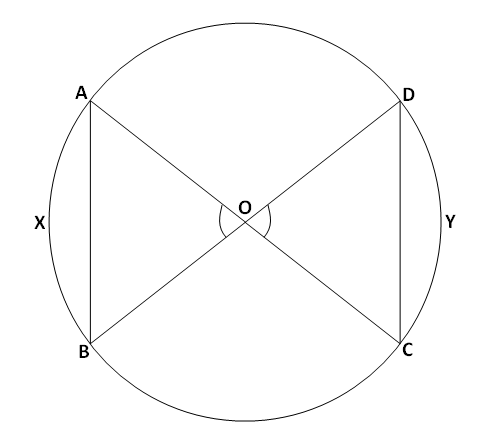
वर दिलेल्या आकृतीत रेख AB आणि रेख CD ह्या वर्तुळाच्या दोन जीवा आहेत. कंस AXB हा जीवा AB शी निगडीत कंस आहे. तसेच कंस CYD हा जीवा CD शी निगडीत कंस आहे.
एकाच वर्तुळाच्या दोन कंसांची मापे समान असतील, तर ते दोन कंस एकरूप असतात.
जेंव्हा वर्तुळाच्या कंसांशी निगडित कोन एकरूप असतात, तेंव्हा ते कंस देखील एकरूप असतात.
जर m\angle AOB=m\angle COD असेल तर m( कंस AXB)=m( कंस CYD)
\therefore कंस AXB\cong कंस CYD
जेंव्हा वर्तुळाचे कंस एकरूप असतात, तेंव्हा त्या कंसांशी निगडित जीवा देखील एकरूप असतात.
जर m\angle AOB=m\angle COD असेल तर \ell ( जीवा AB)=\ell( जीवा CD)
\therefore जीवा AB\cong जीवा CD
जेंव्हा वर्तुळाच्या जीवा एकरूप असतात, तेंव्हा त्या जीवांशी निगडित कंस देखील एकरूप असतात.
जर \ell ( जीवा AB)=\ell( जीवा CD) असेल तर m( कंस AXB)=m( कंस CYD)
\therefore कंस AXB\cong कंस CYD
| 1) एकाच वर्तुळाच्या दोन कंसांची मापे समान असतील, तर ते दोन कंस एकरूप असतात. 2) जेंव्हा वर्तुळाच्या कंसांशी निगडित कोन एकरूप असतात, तेंव्हा ते कंस देखील एकरूप असतात. 3) जेंव्हा वर्तुळाचे कंस एकरूप असतात, तेंव्हा त्या कंसांशी निगडित जीवा देखील एकरूप असतात. 4) जेंव्हा वर्तुळाच्या जीवा एकरूप असतात, तेंव्हा त्या जीवांशी निगडित कंस (लघुकंस आणि विशालकंस) देखील एकरूप असतात. |
वर्तुळाचा कंस उदाहरणे
वर्तुळाची जीवा व कंस ह्या संकल्पना समजावून घेण्यासाठी आपण वर्तुळाच्या कंसाची काही उदाहरणं पाहू,
उदा 1:
केंद्र C असलेल्या वर्तुळाचे रेख AB व रेख CD हे व्यास काटकोनात छेदतात. तर,
(1) कंस AD आणि कंस DB एकरूप का आहेत, हे सांगा .
(2) कंस AD शी एकरूप असलेल्या इतर कंसांची नावे लिहा.
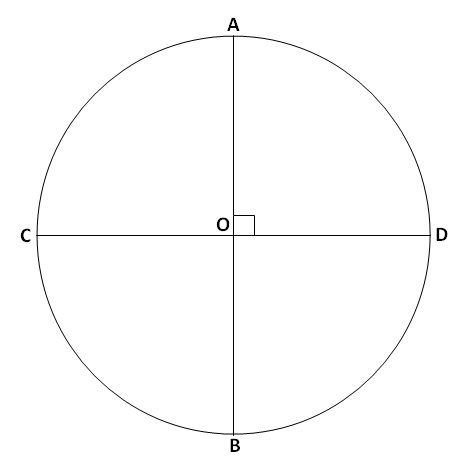
उत्तर:
दिलेल्या आकृतीत वर्तुळाचे व्यास एकमेकांना काटकोनात छेदत आहेत.
\begin{aligned} \\ &\therefore m\angle AOD=m\angle DOB=m\angle BOC=m\angle COA=90^\circ \\ &\therefore \angle AOD\cong \angle DOB\cong \angle BOC\cong \angle COA\end{aligned}
ह्याचा अर्थ वर्तुळाच्या रेख AB आणि रेख CD ह्या दोन व्यासांमुळे तयार होणारे चारही कोन एकरूप असल्याने त्यांच्याशी निगडित चारही कंस एकरूप आहेत.
\therefore कंस AD\cong कंस DB\cong कंस BC\cong कंस CA
(1) कंस AD आणि कंस DB एकरूप आहेत, कारण त्यांच्याशी निगडित कोन \angle AOD आणि \angle DOB एकरूप आहेत.
(2) कंस AD शी एकरूप असलेल्या इतर कंसांची नावे: कंस DB, कंस BC आणि कंस CA
उदा 2:
आकृतीत केंद्र O असलेल्या वर्तुळाचा रेख MN हा व्यास आहे. काही केंद्रीय कोनांची मापे दिली आहेत. त्यावरून
(1) \angle AOB आणि \angle COD यांची मापे काढा.
(2) कंस AB\cong MN कंस CD हे दाखवा.
(3) जीवा AB\cong जीवा CD हे दाखवा.
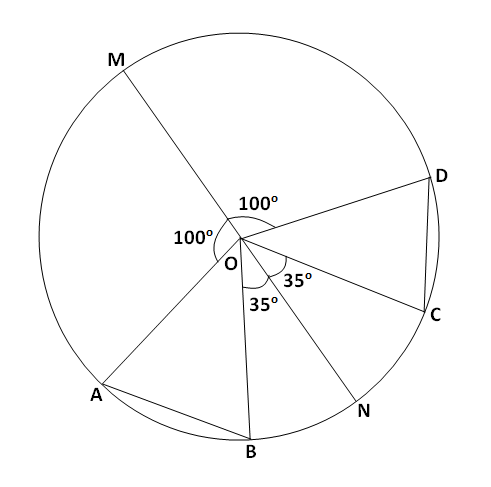
उत्तर:
दिलेल्या आकृतीत व हे वर्तुळाचं केंद्र असून रेख MN हा वर्तुळाचा व्यास आहे.
m\angle AOM+m\angle DOM+m\angle AOB+m\angle COD+m\angle BON+m\angle CON=360^\circ
रेख MN हा वर्तुळाचा व्यास असल्याने हा व्यास वर्तुळाचे दोन सामान अर्धवर्तुळात विभागणी करतो.
\begin{aligned} \\ &\therefore m\angle AOM+m\angle AOB+m\angle BON=180^\circ \\ &\therefore 100^\circ+m\angle AOB+35^\circ=180^\circ \\ &\therefore m\angle AOB+135^\circ=180^\circ \\ &\therefore m\angle AOB=180^\circ-135^\circ \\ &\therefore m\angle AOB=45^\circ\end{aligned}
\begin{aligned} \\ &\therefore m\angle DOM+m\angle COD+m\angle CON=180^\circ \\ &\therefore 100^\circ+m\angle COD+35^\circ=180^\circ \\ &\therefore m\angle COD+135^\circ=180^\circ \\ &\therefore m\angle COD=180^\circ-135^\circ \\ &\therefore m\angle COD=45^\circ\end{aligned}
(1) \mathbf{\therefore m\angle AOB=m\angle COD=45^\circ}
\begin{aligned} \\ &\mathbf{(2)} \therefore m\angle AOB=m\angle COD=45^\circ \\ &\therefore \angle AOB\cong \angle COD\end{aligned}
जेंव्हा वर्तुळाच्या कंसांशी निगडित कोन एकरूप असतात, तेंव्हा ते कंस देखील एकरूप असतात.
\mathbf{\therefore } कंस \mathbf{AB\cong } कंस \mathbf{CD}
(3) कंस AB\cong कंस CD
जेंव्हा वर्तुळाचे कंस एकरूप असतात, तेंव्हा त्या कंसांशी निगडित जीवा देखील एकरूप असतात.
\mathbf{\therefore } जीवा \mathbf{AB\cong } जीवा \mathbf{CD}.
इयत्ता 8 वी गणित पाठ्यपुस्तक: इथे क्लिक करा
