इयत्ता 8 वी त्रिकोणाचे शिरोलंब व मध्यगा म्हणजे काय? : त्रिकोणाचे शिरोलंब व मध्यगा हे महत्त्वाचे घटक आहेत. त्रिकोणाच्या एका शिरोबिंदूपासून समोरच्या बाजूवर टाकलेल्या लंब रेषाखंडाला शिरोलंब म्हणतात, तर कोणत्याही बाजूच्या मध्यबिंदूपासून समोरच्या शिरोबिंदूपर्यंत टाकलेल्या रेषाखंडाला मध्यगा म्हणतात.

त्रिकोणाचे शिरोलंब म्हणजे काय?
त्रिकोणाच्या शिरोबिंदूतून त्याच्या समोरील बाजूवर काढलेल्या लंब रेषाखंडास त्या त्रिकोणाचा शिरोलंब म्हणतात.
| महत्वाचे: शिरोलंब (किंवा लंब रेषाखंड) म्हणजे त्रिकोणाच्या शिरोबिंदूतून सुरु झाल्यानंतर हा रेषाखंड त्रिकोणाच्या समोरच्या बाजूवर काटकोनात छेदतो; म्हणजे छेद बिंदूवर काटकोन (90^\circ अंशाचा कोन) तयार होतो. |

- इथे बिंदू A हा त्रिकोणाचा शिरोबिंदू आहे.
- रेख AP हा शिरोलंब आहे.
- \angle APC हा काटकोन (90^\circ) आहे.
आता आपण त्रिकोणाचे तीनही शिरोलंब काढून त्याचा अभ्यास करूयात,
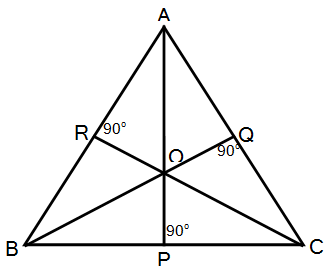
- इथे A, B आणि C हे त्रिकोणाचे 3 शिरोबिंदू आहेत.
- रेख AP, रेख BQ आणि रेख CR हे त्रिकोणाचे 3 शिरोलंब आहेत, म्हणजेच रेख AP \perp रेख BC, रेख BQ \perp रेख AC आणि रेख CR \perp रेख AB.
- हे तीनही शिरोलंब एकाच बिंदूत (बिंदू O) एकमेकांना छेदतात; म्हणून हे तीनही शिरोलंब एकसंपाती आहेत, असं म्हणतात.
- आणि ह्या बिंदूला त्रिकोणाचा शिरोलंबसंपात किवा लंबसंपात बिंदू असे म्हणतात आणि तो ‘O’ या अक्षराने दर्शवतात.
आता आपण वेगवेगळ्या त्रिकोणांचे शिरोलंबसंपात बिंदूचे स्थान कुठे असते, ते पाहुयात,
काटकोन त्रिकोण
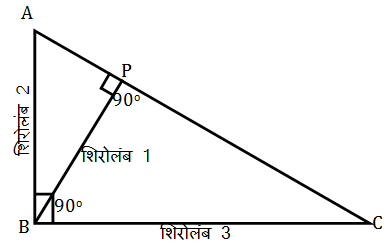
शेजारच्या काटकोन त्रिकोणात B ह्या शिरोबिंदूतून आपण रेख BP हा शिरोलंब रेख AC वर काढला आहे. इथे P हा छेदबिंदू आहे. आता लक्षात घ्या की रेख BP हा शिरोलंब असल्याने P ह्या बिंदूवर तो रेख AC ला काटकोनात म्हणजेच 90^\circ अंशात छेदतो आहे.
| महत्वाचे: अजून एक लक्षात घ्या की काटकोन त्रिकोणात रेख BP प्रमाणे शिरोबिंदू A आणि C मधून त्यांच्या समोरच्या रेख BC आणि रेख AB वर शिरोलंब काढता येत नाहीत; कारण जर आपण A किंवा C शिरोबिंदूमधून समोरच्या रेख BC किंवा रेख AB वर रेषाखंड काढण्याचा प्रयत्न केला तर ते रेषाखंड रेख AB किंवा रेख BC ला काटकोनात छेदू शकत नाहीत. |
मग आता काटकोन त्रिकोणाचे राहिलेले दोन शिरोलंब काढायचे कसे?
ह्याचं उत्तर अगदी सोपं आहे, कारण ते दोन शिरोलंब आपण आधीच काढलेले आहेत. हो, खरंच, आपण ते आधीच काढलेले आहेत.
ते दोन शिरोलंब आहेत रेख AB आणि रेख CB. म्हणजे काटकोन त्रिकोणात त्याच्या दोन बाजूच त्याचे दोन शिरोलंब असतात. आता ते कसं ते आपण समजावून घेऊ,
सोबतच्या आकृतीचं लक्ष देऊन निरीक्षण करा. सोबतच्या आकृतीत रेख AB हा रेख BC वर काढलेला शिरोलंब आहे, कारण तो रेख BC ला B ह्या बिंदूत काटकोनात (म्हणजे 90 अंशात) छेदतो आहे.
तसेच रेख CB हा रेख AB वर काढलेला शिरोलंब आहे, कारण तो रेख AB ला B ह्या बिंदूत काटकोनात (म्हणजे 90 अंशात) छेदतो आहे. तेंव्हा बिंदू B हा काटकोन त्रिकोणाचा शिरोलंबसंपात किवा लंबसंपात बिंदू आहे.
विशालकोन त्रिकोण

विशालकोन त्रिकोणाची गंमत थोडी वेगळी आहे; पण समजायला अजिबात अवघड नाही.
वरील आकृतीत \triangle ABC हा विशालकोन त्रिकोण आहे.
आपण बिंदू B पासून समोरच्या रेख AC वर रेख BP हा शिरोलंब टाकलेला आहे आणि हा ह्या विशालकोन त्रिकोणाचा पहिला शिरोलंब आहे.
पण बिंदू A आणि बिंदू C पासून त्यांच्या समोरच्या बाजूंवर (म्हणजे रेख BC आणि रेख AB) शिरोलंब टाकता येत नाहीत, कारण ते समोरच्या बाजूंना काटकोनात छेदू शकत नाहीत.
मग आता करायचं काय? विशालकोन त्रिकोणाचा लंबसंपात बिंदू शोधायचा कसा? तर ह्याचं उत्तर अगदी सोपं आहे, ते शेजारील आकृतीचं नीट निरीक्षण केल्यावर तुमच्या लक्षात येईलच. मित्रांनो, एकदा ही आकृती तुम्हाला नीट समजली आणि पक्की लक्षात राहिली की तुमचं 95% काम झालेलं आहे; राहिलेलं 5% टक्के काम हे आहे की खाली दिलेलं आकृतीचं वर्णन समजावून घेऊन परीक्षेत तुम्हाला लिहिता यायला पाहिजे.
आता आपण हा लंबसंपात बिंदू शोधण्यासाठी इथे काय केलंय ते समजावून घेऊयात,
- आपण बाजू AB ला तसेच पुढे बिंदू R पर्यंत वाढवले आहे.
- तसेच आपण बाजू CB ला बिंदू Q पर्यंत पुढे वाढवले आहे.
- त्यानंतर आपण बिंदू A पासून एक रेषा काढली आहे, जी रेख CQ ला बिंदू Q मध्ये काटकोनात छेदते आहे आणि तशीच पुढे बिंदू O पर्यंत जात आहे.
- महत्वाचं: म्हणजेच रेख AQ हा बिंदू A पासून समोरच्या रेख CQ वर टाकलेला ह्या विशालकोन त्रिकोणाचा दुसरा शिरोलंब आहे.
- वरील प्रमाणेच आपण बिंदू C पासून एक रेषा काढली आहे ती रेख AR ला बिंदू R मध्ये काटकोनात छेदते आहे आणि तशीच पुढे बिंदू O पर्यंत जात आहे.
- महत्वाचं: म्हणजेच रेख CR हा बिंदू C पासून समोरच्या रेख AR वर टाकलेला ह्या विशालकोन त्रिकोणाचा तिसरा शिरोलंब आहे.
- आपण वर पहिलेच आहे की बिंदू B पासून त्याच्या समोरच्या रेख AC वर शिरोलंब BP टाकलेला आहे. हा रेख BP शिरोलंब आपण तसाच मागे वाढवला तर तो देखील बिंदू O मधून जातो.
- ह्याचा अर्थ विशालकोन त्रिकोणाचे तीनही शिरोलंब रेख AQ, रेख CR आणि रेख PB हे पुढे वाढवले असता एकमेकांना बिंदू O मध्ये छेदतात, म्हणून बिंदू O हा विशालकोन त्रिकोणाचा शिरोलंबसंपात किवा लंबसंपात बिंदू आहे.
| महत्वाचं: म्हणजेच विशालकोन त्रिकोणाचा शिरोलंबसंपात किवा लंबसंपात बिंदू हा त्या त्रिकोणाच्या बाह्य भागात असतो. |
लघुकोन त्रिकोण
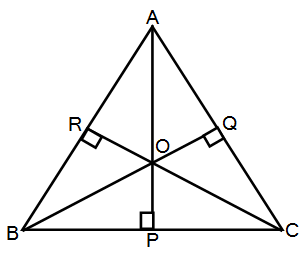
इथे A, B आणि C हे त्रिकोणाचे 3 शिरोबिंदू आहेत.
रेख AP, रेख BQ आणि रेख CR हे त्रिकोणाचे 3 शिरोलंब आहेत, म्हणजेच
रेख AP\perp रेख BC,
रेख BQ\perp रेख AC आणि
रेख CR\perp रेख AB.
हे तीनही शिरोलंब बिंदू O ह्या एकाच बिंदूत एकमेकांना छेदतात; म्हणून बिंदू O हा लघुकोनत्रिकोणाचा शिरोलंबसंपात किवा लंबसंपात बिंदू आहे.
| थोडक्यात: 1) त्रिकोणाचे शिरोलंब हे एकसंपाती असतात, म्हणजेच ते एकाच बिंदूतून जातात. त्या बिंदूला “लंबसंपात बिंदू” असं म्हणतात आणि हा बिंदू इंग्रजी “O” (ओ) ह्या अक्षराने दाखवायची पद्धत आहे. 2) काटकोन त्रिकोणाचा लंबसंपात बिंदू हा काटकोन करणाऱ्या शिरोबिंदूवर असतो. 3) विशालकोन त्रिकोणाचा लंबसंपात बिंदू हा त्या त्रिकोणाच्या बाह्यभागात असतो. 4) लघुकोन त्रिकोणाचा लंबसंपात बिंदू हा त्या कोणाच्या अंतर्भागात असतो. |
त्रिकोणाची मध्यगा म्हणजे काय?
त्रिकोणाचा शिरोबिंदू आणि त्या समोरील बाजूच्या मध्य बिंदूला जोडणाऱ्या रेषाखंडाला त्या त्रिकोणाची मध्यगा असं म्हणतात.

\triangle ABC मध्ये रेख AR, रेख BP आणि रेख CQ ह्या त्या त्रिकोणाच्या मध्यगा आहेत. आणि त्यामुळे,
- \ell(AP)=\ell(PC) … कारण बिंदू P हा रेख AC चा मध्यबिंदू आहे.
- \ell(AQ)=\ell(QB) … कारण बिंदू Q हा रेख AB चा मध्यबिंदू आहे.
- \ell(BR)=\ell(RC) … कारण बिंदू R हा रेख BC चा मध्यबिंदू आहे.
| महत्वाचं: 1) इथे एक लक्षात घ्या की त्रिकोणाच्या मध्यगा ह्या एकाच बिंदूतून जातात आणि ह्या बिंदूला “मध्यगासंपात” असं म्हणतात आणि तो बिंदू इंग्रजी “G” ह्या अक्षराने दर्शविण्याची पद्धत आहे. 2) त्यामुळे त्रिकोणाच्या मध्यगा ह्या “एकसंपाती” असतात, असं म्हटलं जातं. 3) कोणत्याही त्रिकोणाचा मध्यगासंपात (संपात बिंदू G) हा नेहमी त्या त्रिकोणाच्या अंतर्भागात असतो. 4) मध्यगासंपातमुळे (संपात बिंदू G मुळे) प्रत्येक मध्यगेचे 2:1 या गुणोत्तरात विभाजन होते. |
आता आपण काटकोन त्रिकोण, विशालकोन त्रिकोण आणि लघुकोन त्रिकोण ह्यांच्या मध्यगा काढून बघू,
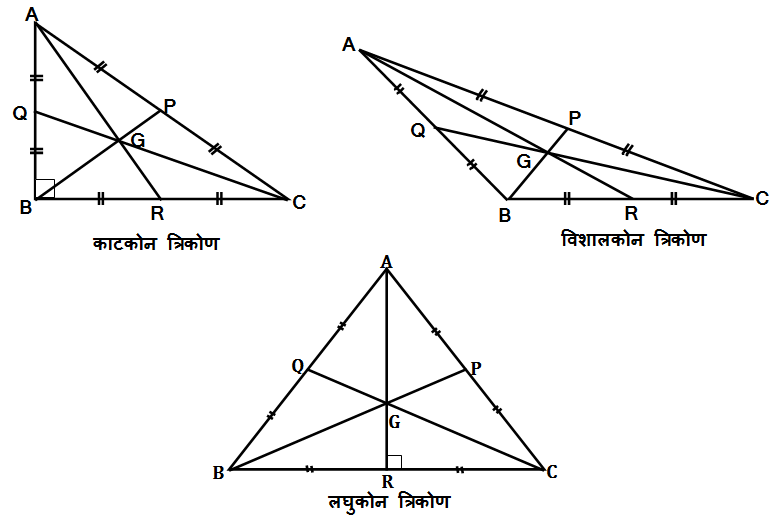
आता आपण एक त्रिकोण घेऊन त्याच्या मध्यगा काढू आणि त्याची निरीक्षणं नोंदवू,
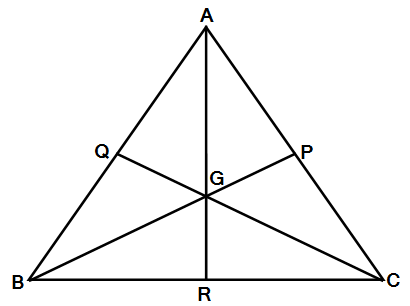
शेजारच्या आकृतीतील त्रिकोण हा समभुज त्रिकोण आहे.
∴ \ell(AB)=\ell(BC)=\ell(AC)=6 सें.मी.
रेख AR, रेख BP आणि रेख CQ ह्या त्रिकोणाच्या मध्यगा आहेत.
- \ell(AQ)=\ell(QB)=3 सें.मी.,
- \ell(BR)=\ell(RC)=3 सें.मी. आणि
- \ell(AP)=\ell(PC)=3 सें.मी.
वरील त्रिकोण समभुज त्रिकोण असल्याने त्याच्या तीनही मध्यगांची लांबी समान आहे.
\therefore \ell(AR)=\ell(BP)=\ell(CQ)=5.2 सें.मी.
त्रिकोणाच्या प्रत्येक मध्यगेची मध्यगासंपात बिंदूमुळे दोन रेषाखंडात खालील प्रमाणे विभागणी होत आहे,
- मध्यगा रेख AR ची रेख AG आणि रेख GR अशी विभागणी होत आहे.
- मध्यगा रेख BP ची रेख BG आणि रेख GP अशी विभागणी होत आहे.
- मध्यगा रेख CQ ची रेख CG आणि रेख GQ अशी विभागणी होत आहे.
आता आपण ह्या विभागलेल्या सर्व रेषाखंडांची लांबी पट्टीने मोजून त्याची निरीक्षण लिहुयात,
- \ell(AG)=3.5 सें.मी. आणि \ell(GR)=1.7 सें.मी. म्हणजेच \ell(AG)=2 \times \ell(GR)
- \ell(BG)=3.5 सें.मी. आणि \ell(GP)=1.7 सें.मी. म्हणजेच \ell(BG)=2 \times \ell(GP)
- \ell(CG)=3.5 सें.मी. आणि \ell(GQ)=1.7 सें.मी. म्हणजेच \ell(CG)=2 \times \ell(GQ)
| महत्वाचं: म्हणजेच त्रिकोणाच्या मध्यगासंपात बिंदूमुळे 2:1 ह्या प्रमाणात मध्यगांची विभागणी होते. |
शिरोलंब व मध्यगा ह्यांच्यातला फरक
| अनुक्रमांक | शिरोलंब | मध्यगा |
|---|---|---|
| 1. | शिरोलंब हा त्रिकोणाच्या शिरोबिंदूपासून त्याच्या समोरच्या बाजूवर टाकलेला लंब असतो. | मध्यगा त्रिकोणाचा शिरोबिंदू आणि त्याच्या समोरच्या बाजूचा मध्य, ह्यांना जोडते. |
| 2. | शिरोलंब त्रिकोणाच्या शिरोबिंदूच्या समोरच्या बाजूला नेहमी 90 अंशात छेदतो. | मध्यगा त्रिकोणाच्या शिरोबिंदूच्या समोरच्या बाजूला 90 अंशात छेदेलच, असं नाही. |
| महत्वाचं: समभुज त्रिकोणात त्या त्रिकोणाचे शिरोलंब व मध्यगा ह्या एकच असतात आणि त्यामुळे लंबसंपात आणि मध्यगासंपात बिंदूही एकच असतो. |
शिरोलंब व मध्यगा यांची उदाहरणे
उदाहरण 1:
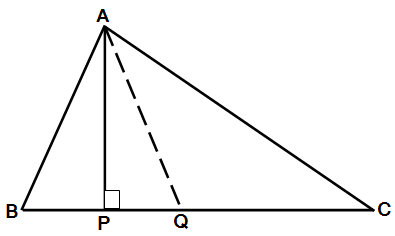
शेजारच्या \triangle ABC मध्ये रेख AP हा शिरोबिंदू A पासून समोरची बाजू रेख BC वर टाकलेला शिरोलंब आहे, कारण तो रेख BC ला बिंदू P मध्ये काटकोनात छेदत आहे.
बिंदू Q हा रेख BC चा मध्यबिंदू आहे आणि त्यामुळे रेख AQ ही \triangle ABC ची मध्यगा आहे.
उदाहरण 2:
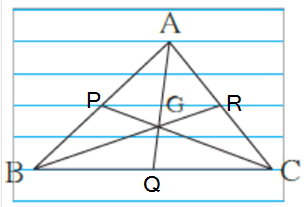
एका विद्यार्थ्याने वहीच्या कागदावरील पाच समांतर रेषा वापरून \triangle ABC काढला व G हा मध्यगासंपात शोधला. तर त्याने ठरवलेले G चे स्थान बरोबर आहे, हे कसे ठरवाल?
उत्तर:
वरील आकृतीत \triangle ABC मध्ये जर
\begin{aligned} \\ & \ell(AP)=\ell(PB), \\ & \ell(BQ)=\ell(QC), \\ & \ell(AR)=\ell(RC)\end{aligned}
आणि
\begin{aligned} \\ & \ell(AG)=2\times \ell(GQ), \\ & \ell(BG)=2\times \ell(GR), \\ & \ell(CG)=2\times \ell(GP)\end{aligned}
असेल तर आणि \triangle ABC च्या तीनही मध्यगा एकमेकींना G ह्या एकाच बिंदूत छेदत (एकसंपाती) असतील तर, त्या विद्यार्थ्याने ठरवलेले G चे स्थान योग्य आहे.
उदाहरण 3:
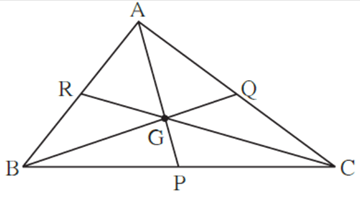
\triangle ABC चा G हा मध्यगासंपातबिंदू आहे.
जर \ell (RG)=2.5 तर \ell (GC)=5
जर \ell (BG)=6 तर \ell (BQ)=9
कारण आपण आधीच पहिले आहे की मध्यगासंपातबिंदूमुळे मध्यगांचे 2:1 ह्या प्रमाणात विभाजन होते.
उदाहरण 4:
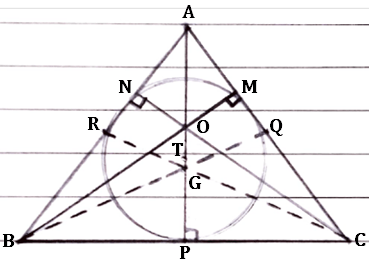
- \triangle ABC हा समद्विभुज त्रिकोण आहे.
- \therefore \ell (AB)=\ell (AC)
- रेख AP, रेख BM आणि रेख CN हे \triangle ABC चे शिरोलंब आहेत आणि O हा लंबसंपात बिंदू आहे.
- रेख AP, रेख BQ आणि रेख CR ह्या \triangle ABC च्या मध्यगा आहेत आणि G हा मध्यगासंपात बिंदू
| त्रिकोणाचे शिरोलंब व मध्यगा: त्रिकोणाच्या एका शिरोबिंदूपासून समोरच्या बाजूवर टाकलेला लंब रेषाखंड म्हणजे शिरोलंब. प्रत्येक त्रिकोणाला तीन शिरोलंब असतात, आणि ते “शिरोलंबसंपात किवा लंबसंपात” या बिंदूवर एकत्र येतात. आणि त्रिकोणाच्या कोणत्याही बाजूच्या मध्यबिंदूपासून समोरच्या शिरोबिंदूपर्यंत टाकलेला रेषाखंड म्हणजे मध्यगा. त्रिकोणाच्या तीन मध्यगा एका बिंदूत छेदतात, त्या बिंदुला “मध्यगासंपात” म्हणतात. शिरोलंब व मध्यगा हे त्रिकोणाचे अत्यंत महत्वाचे घटक आहेत. समभुज त्रिकोणात शिरोलंब व मध्यगा समान बिंदूत एकत्र येतात. समलंब त्रिकोणात आधारभुजेवरील शिरोलंब व मध्यगा एकाच सरळ रेषेत असतात. इतर प्रकारच्या त्रिकोणांमध्ये शिरोलंब व मध्यगा वेगवेगळ्या प्रकारे स्थित असतात, ज्या विषयी आपण वर चर्चा केली आहे. शिरोलंब व मध्यगा हे त्रिकोणी आकाराच्या बांधणीच्या स्थिरतेसाठी आणि विविध गणितीय सिद्धांतांसाठी आवश्यक घटक आहेत. अभियांत्रिकी, खगोलशास्त्र, वास्तुकला आणि गणितीय संशोधनात शिरोलंब व मध्यगा अत्यंत महत्त्वाचे आहेत. शिरोलंब व मध्यगा या संकल्पना त्रिकोणाच्या अभ्यासात अत्यंत महत्त्वाच्या आहेत. त्यामुळे, शिरोलंब व मध्यगा यांचा सखोल अभ्यास करणे उपयुक्त ठरेल. शिरोलंब व मध्यगा यांचे उपयोग आणि वैशिष्ट्ये समजून घेतल्यास त्रिकोणाची भूमिती अधिक स्पष्ट होते. |
इयत्ता 8 वीचे पाठयपुस्तक: इथे क्लिक करा
