इयत्ता 8 वी संकीर्ण प्रश्नसंग्रह 2 हा बहुपदींचा भागाकार, सांख्यिकी, एकचल समीकरणे, त्रिकोणांची एकरूपता, चक्रवाढ व्याज, क्षेत्रफळ, पृष्ठफळ व घनफळ आणि वर्तुळाच्या जीवा आणि कंस या विषयांवरील उजळणी प्रश्नसंग्रह आहे.

संकीर्ण प्रश्नसंग्रह 2
प्रश्नसंग्रह : उदाहरण 1
पुढील प्रश्नांसाठी पर्यायी उत्तरे दिली आहे. त्यांपैकी योग्य पर्याय निवडा.
(1) एका वर्तुळाचे क्षेत्रफळ 1386 चौसेमी असेल तर त्याचा परीघ किती असेल?
(A) 132 चौसेमी
(B) 132 सेमी
(C) 42 सेमी
(D) 21 चौसेमी
उत्तर:
वर्तुळाचं क्षेत्रफळ A=\pi \times r^2
\begin{aligned} \\ &\therefore 1386=\frac{22}{7}\times r^2 \\ &\therefore r^2=1386\times \frac{7}{22} \\ &\therefore r^2=63\times 7 \\ &\therefore r^2=441 \\ &\therefore \sqrt{r^2}=\sqrt{441} \\ &\therefore r=21\end{aligned}
वर्तुळाचा परीघ P=2\times \pi \times r
\begin{aligned} \\ &\therefore P=2\times \frac{22}{7}\times 21 \\ &\therefore P=2\times 22\times 3 \\ &\therefore P=132\end{aligned}
\mathbf{\therefore } पर्याय B ग्राह्य आहे.
(2) एका घनाची बाजू 4 मी आहे. ती दुप्पट केली तर त्याचे घनफळ किती पटीने वाढेल?
(A)दोन पटीने
(B) तीन पटीने
(C) चार पटीने
(D)आठ पटीने
उत्तर:
घनाचे घनफळ V_1= बाजू \times बाजू \times बाजू
\begin{aligned} \\ &\therefore V_1=4\times 4\times 4\\ &\therefore V_1=64\end{aligned}
जर घनाच्या बाजूची लांबी दुप्पट केली तर बाजूची लांबी 4\times 2=8 मी होईल.
\therefore घनाचे घनफळ V_2= बाजू \times बाजू \times बाजू
\begin{aligned} \\ &\therefore V_2=8\times 8\times 8\\ &\therefore V_2=512\end{aligned}
\begin{aligned} \\ &\therefore \frac{512}{64}=8 \\ &\therefore V_2=8\times V_1\end{aligned}
\mathbf{\therefore } पर्याय D ग्राह्य आहे.
प्रश्नसंग्रह : उदाहरण 2
प्रणाली 100 मीटर धावण्याच्या शर्यतीचा सराव करत होती. त्यासाठी ती 100 मीटर अंतर 20 वेळा धावली. प्रत्येक वेळी त्यासाठी लागलेला वेळ सेकंदांत खालील प्रमाणे होता.
18 , 17 , 17 , 16 , 15 , 16 , 15 , 14 , 16 , 15 , 15 , 17 , 15 , 16 , 15 , 17 , 16 , 15 , 14 , 15 धावण्यासाठी तिला लागलेल्या वेळांचा मध्य काढा.
उत्तर:
प्रणालीने 100 मीटर अंतर 20 वेळा धावून नोंदवलेल्या वेळांची सरासरी (मध्य) आपल्याला काढायची आहे.
सरासरी = नोंदवलेल्या वेळांची बेरीज / नोंदवलेल्या एकूण वेळा
\begin{aligned} \\ &=\frac{18+17+17+16+15+16+15+14+16+15+15+17+15+16+15+17+16+15+14+15}{20} \\ &=\frac{314}{20} \\ &=15.7\end{aligned}
प्रणालीने 100 मीटर अंतर 20 वेळा धावून नोंदवलेल्या वेळांची सरासरी (मध्य) 15.7 आहे.
प्रश्नसंग्रह : उदाहरण 3
\triangle DEF आणि \triangle LMN हे त्रिकोण EDF\leftrightarrow LMN या एकास एक संगतीत एकरुप आहेत. तर या संगतीनुसार होणाऱ्या एकरुप बाजूंच्या आणि एकरुप कोनांच्या जोड्या लिहा.
उत्तर:

आकृतीत \triangle DEF आणि \triangle LMN. हे त्रिकोण EDF\leftrightarrow LMN या एकास एक संगतीत एकरुप आहेत. ह्या संगतीने एकरूप होणारे ह्या दोन त्रिकोणाचे कोन आणि बाजू सारख्या खुणांनी दर्शवलेल्या आहेत. आणि त्याप्रमाणे आपल्याला खालील एकरूपता मिळते,
\begin{aligned} \\ &(1)\;\angle D\cong \angle M \\ &(2)\;\angle E\cong \angle L \\ &(1)\;\angle F\cong \angle N\end{aligned}
(1) बाजू DE\cong बाजू LM
(2) बाजू EF\cong बाजू LN
(3) बाजू DF\cong बाजू MN
प्रश्नसंग्रह : उदाहरण 4
एका यंत्राची किंमत 2,50,000 रुपये आहे. ती दरसाल 4% दराने घटते. तर यंत्र घेतल्यापासून तीन वर्षांनी त्या यंत्राची किंमत किती असेल?
उत्तर:
आधी या उदाहरणात काय दिलेलं आहे, ते आपण लिहून घेऊ,
यंत्राची किंमत P = 2,50,000
घसाऱ्याचा दर R = – 4%
कालावधी N = 3
आता रापण चक्रवाढ व्याजाचं रास काढण्याचं सूत्र वापरून हे उदाहरण सोडवुया,
\begin{aligned} \\ &A=P\times \left(1+\frac{R}{100}\right)^N \\ &\therefore A=2,50,000\times \left(1+\frac{-4}{100}\right)^3 \\ &\therefore A=2,50,000\times \left(\frac{100-4}{100}\right)^3 \\ &\therefore A=2,50,000\times \left(\frac{96}{100}\right)^3 \\ &\therefore A=2,50,000\times \left(0.96\right)^3 \\ &\therefore A=2,50,000\times \left(0.884736\right) \\ &\mathbf{\therefore A=2, 21, 184}\end{aligned}
\mathbf{\therefore } यंत्र घेतल्यापासून तीन वर्षांनी त्या यंत्राची किंमत 2, 21, 184 रुपये असेल.
प्रश्नसंग्रह : उदाहरण 5
\square ABCD मध्ये बाजू AB\parallel बाजू DC, रेख AE\perp बाजू DC. जर \ell\left(AB\right)=9 सेमी, \ell\left(AE\right)=10 सेमी, A\left(\square ABCD\right)=115 सेमी ^2, तर \ell\left(DC\right) काढा.
उत्तर:
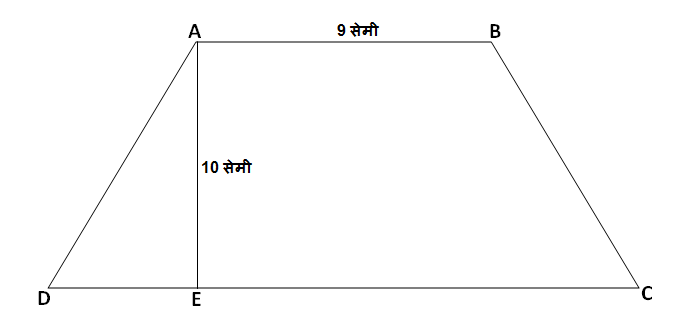
दिलेला चौकोन हा समलंब चौकोन आहे.
समलंब चौकोनाचं क्षेत्रफळ A=\frac{1}{2}\times (समांतर असलेल्या बाजूंच्या लांबींची बेरीज) \times (उंची)
\begin{aligned} \\ &\therefore A=\frac{1}{2}\times \left[\ell\left(AB\right)+\ell\left(DC\right)\right]\times h \\ &\therefore 115=\frac{1}{2}\times \left[\left(9\right)+\ell\left(DC\right)\right]\times 10 \\ &\therefore 115=\left[\left(9\right)+\ell\left(DC\right)\right]\times 5 \\ &\therefore \frac{115}{5}=9+\ell\left(DC\right) \\ &\therefore 23=9+\ell\left(DC\right) \\ &\therefore \ell\left(DC\right)=23-9 \\ &\therefore \ell\left(DC\right)=14\end{aligned}
\mathbf{\therefore \ell\left(DC\right)=14} सेमी.
प्रश्नसंग्रह : उदाहरण 6
वृत्तचिती आकाराच्या एका टाकीच्या तळाचा व्यास 1.75 मी आणि उंची 3.2 मी आहे. तर त्या टाकीची क्षमता किती लीटर आहे? \pi=\frac{22}{7}.
उत्तर:
(1) टाकीच्या तळाची त्रिज्या r = (टाकीच्या तळाचा व्यास) / 2 =\frac{1.75}{2}=0.875 मी
(2) टाकीची खोली/उंची h = 3.2 मी
टाकीचं घनफळ V=\pi r^2\times h
\begin{aligned} \\ &\therefore V=\frac{22}{7}\times 0.875^2\times 3.2 \\ &\therefore V=\frac{22}{7}\times 0.765625\times 3.2 \\ &\therefore V=\frac{22}{7}\times 2.45 \\ &\therefore V=22\times 0.35 \\ &\therefore V=7.7\end{aligned}
टाकीचं घनफळ 7.7 घन मी आहे.
1000 घन सेमी = 1000 मिली = 1 लिटर
1 घन मीटर = 100\times 100\times 100=10,00,000 घन सेमी = 10,00,000 मिली = \frac{10,00,000}{1000}=1000 लिटर
\therefore 7.7 घन मी = 7.7\times 1000=7700 लिटर
टाकीची क्षमता 7700 लिटर आहे.
प्रश्नसंग्रह : उदाहरण 7
त्रिज्या 9.1 सेमी असलेल्या वर्तुळाच्या एका जीवेची लांबी 16.8 सेमी आहे. तर ती जीवा केंद्रापासून किती अंतरावर आहे?

उत्तर:
वरील आकृतीत दाखवल्याप्रमाणे वर्तुळाची त्रिज्या, जीवा आणि जीवेचं वर्तुळाच्या केंद्रापासूनचं अंतर, हे मिळून \triangle CPB हा काटकोन त्रिकोण तयार झालेला आहे.
आपल्याला माहित आहे की वर्तुळाच्या केंद्रातून जीवेवर टाकलेला लंब जीवेला दुभागतो; म्हणजे जीवेची दोन समान लांबीच्या रेषाखंडात विभागणी करतो.
\therefore \ell\left(AP\right)=\ell\left(BP\right) आणि जीवा \ell\left(AB\right)=\ell\left(AP\right)+\ell\left(BP\right)=2\times \ell\left(BP\right)
\begin{aligned} \\ &\therefore 2\times \ell\left(BP\right)=\ell\left(AB\right) \\ &\therefore 2\times \ell\left(BP\right)=16.8 \\ &\therefore \ell\left(BP\right)=\frac{1}{2}\times 16.8 \\ &\therefore \ell\left(BP\right)=8.4\end{aligned}
\triangle CPB हा काटकोन त्रिकोण असल्याने आपण पायथॅगोरसच्या सूत्राने आता रेख CP ची लांबी काढू,
पायथॅगोरसच्या सूत्राप्रमाणे,
\begin{aligned} \\ &\therefore \ell\left(CB\right)^2=\ell\left(CP\right)^2+\ell\left(BP\right)^2 \\ &\therefore \left(9.1\right)^2=\ell\left(CP\right)^2+\left(8.4\right)^2 \\ &\therefore 82.81=70.56+\ell\left(CP\right)^2 \\ &\therefore \ell\left(CP\right)^2=82.81-70.56 \\ &\therefore \ell\left(CP\right)^2=12.25 \\ &\therefore \sqrt{\ell\left(CP\right)^2}=\sqrt{12.25} \\ &\therefore \ell\left(CP\right)=3.5\end{aligned}
\mathbf{\therefore }जीवा \mathbf{AB} वर्तुळ केंद्र \mathbf{C} पासून 3.5 सेमी अंतरावर आहे.
प्रश्नसंग्रह : उदाहरण 8
रोजगार हमी योजनेखाली A, B, C, D या गावांत सुरु असलेल्या कामांवरील पुरुष व स्त्री कामगारांची संख्या खालील सारणीत दिली आहे.
| गाव | A | B | C | D |
|---|---|---|---|---|
| स्त्रिया | 150 | 240 | 90 | 140 |
| पुरुष | 225 | 160 | 210 | 110 |
| एकूण कामगार | 375 | 400 | 300 | 250 |
| स्त्री कामगारांचं शतमान | \frac{150}{375}\times 100=40 | \frac{240}{400}\times 100=60 | \frac{90}{300}\times 100=30 | \frac{140}{250}\times 100=56 |
| पुरुष कामगारांचं शतमान | \frac{225}{375}\times 100=60 | \frac{160}{400}\times 100=40 | \frac{210}{300}\times 100=70 | \frac{110}{250}\times 100=44 |
उत्तर:
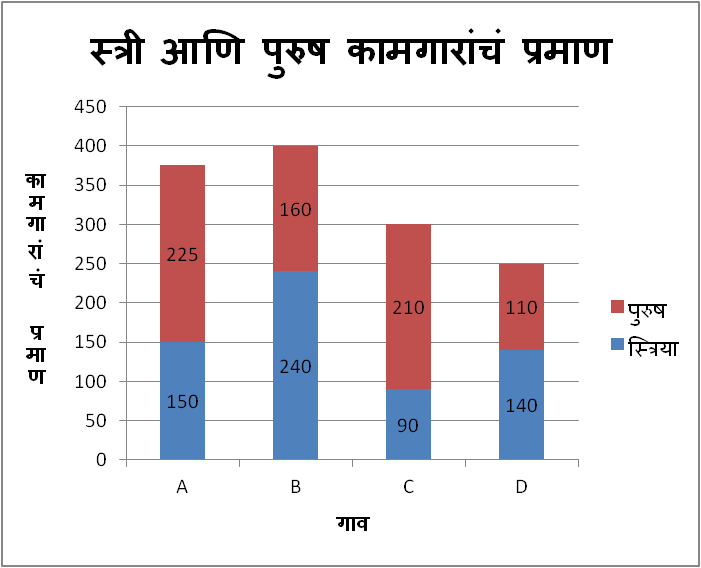
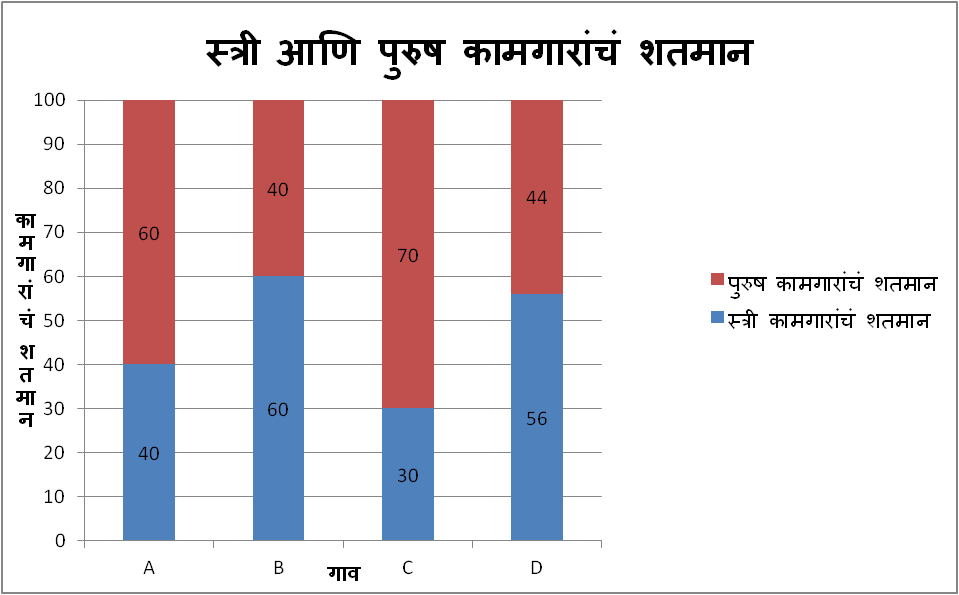
प्रश्नसंग्रह : उदाहरण 9
पुढील समीकरणं सोडवा,
\begin{aligned} \\ &(1)\;17\left(x+4\right)+8\left(x+6\right)=11\left(x+5\right)+15\left(x+3\right) \\ &\therefore 17x+68+8x+48=11x+55+15x+45 \\ &\therefore 25x+116=26x+100 \\ &\therefore 25x+116-25x=26x+100-25x \\ &\therefore 116=x+100 \\ &\therefore 116-100=x+100-100 \\ &\therefore 16=x \\ &\mathbf{\therefore x=16}\end{aligned}
\begin{aligned} \\ &(2)\;\frac{3y}{2}+\frac{y+4}{4}=5-\frac{y-2}{4} \\ &\therefore \frac{6y+y+4}{4}=5-\frac{y-2}{4} \\ &\therefore \frac{7y+4}{4}=5-\frac{y-2}{4} \\ &\therefore \frac{7y+4}{4}+\frac{y-2}{4}=5-\frac{y-2}{4}+\frac{y-2}{4} \\ &\therefore \frac{7y+4+y-2}{4}=5 \\ &\therefore 4\times \frac{7y+4+y-2}{4}=5\times 4 \\ &\therefore 8y+2=20 \\ &\therefore 8y+2-2=20-2 \\ &\therefore 8y=18 \\ &\therefore \frac{1}{8}\times 8y=\frac{1}{8}\times 18 \\ &\mathbf{\therefore y=\frac{9}{4}}\end{aligned}
\begin{aligned} \\ &(3)\;5\left(1-2x\right)=9\left(1-x\right) \\ &\therefore 5-10x=9-9x \\ &\therefore 5-10x+9x=9-9x+9x \\ &\therefore 5-x=9 \\ &\therefore 5-x-5=9-5 \\ &\therefore -x=4 \\ &\therefore -1\times -x=-1\times 4 \\ &\mathbf{\therefore x=-4}\end{aligned}
प्रश्नसंग्रह : उदाहरण 10
पुढील कृती दिलेल्या पायऱ्यांनुसार करा.
(1)समभुज \square ABCD आणि त्याचा कर्ण AC काढा.
(2) एकरुप घटक समान चिन्हाने दाखवा.
(3) \triangle ADC व \triangle ABC कोणत्या संगतीत व कोणत्या कसोटीने एकरुप होतात ते लिहा.
(4) \angle DCA\cong \angle BCA, तसेच \angle DAC\cong \angle BAC दाखवण्यासाठी कारण लिहा.
(5) वरील पायऱ्यांवरून लक्षात येणारा समभुज चौकोनाचा गुणधर्म लिहा.
उत्तर:
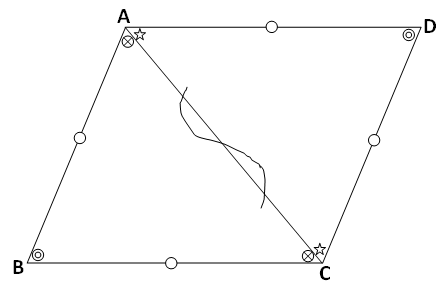
(1) वरील आकृतीत \square ABCD हा समभुज चौकोन आहे. रेख AC हा चौकोन \square ABCD चा कर्ण आहे.
(2) \square ABCD च्या एकरूप बाजू आणि एकरूप कोन सारख्या खुणांनी दर्शवलेल्या आहेत.
(3) समभुज चौकोनाच्या कर्णामुळे आपल्याला \triangle ABC आणि \triangle ADC असे दोन त्रिकोण मिळतात.
\triangle ABC आणि \triangle ADC च्या खाली दिलेल्या बाबी एकरूप आहेत,
\ell\left(AB\right)=\ell\left(AD\right)\;\therefore बाजू AB\cong बाजू AD
\ell\left(BC\right)=\ell\left(DC\right)\;\therefore बाजू BC\cong बाजू DC
\ell\left(AC\right)=\ell\left(AC\right)\;\therefore बाजू AC\cong बाजू AC … सामाईक बाजू
m\angle ABC=m\angle ADC\;\therefore \angle ABC\cong \angle ADC
m\angle BAC=m\angle DAC\;\therefore \angle BAC\cong \angle DAC
m\angle BCA=m\angle DCA\;\therefore \angle BCA\cong \angle DCA
त्यामुळे \triangle ABC आणि \triangle ADC,
(i) ABC\leftrightarrow ADC संगतीने आणि
(ii) बा-बा-बा कसोटीने एकरूप आहेत.
(4) समभुज चौकोनाचा कर्ण त्याच्या संमुख कोनांना दुभागतो, म्हणजे त्याच्या कोनांची दोन सारख्या मापांच्या कोनांमध्ये विभागणी करतो.
\therefore m\angle BAC=m\angle DAC आणि m\angle BCA=m\angle DCA
\therefore \angle BAC\cong \angle DAC आणि \angle BCA\cong \angle DCA
(5) वरील चार पायऱ्यांवरून आपण खालील निष्कर्ष काढू शकतो,
(i) समभुज चौकोनाचे संमुख कोन एकरूप असतात.
(ii) समभुज चौकोनाचा कर्ण त्याच्या संमुख कोनांना दुभागतो, म्हणजे त्याच्या कोनांची दोन सारख्या मापांच्या कोनांमध्ये विभागणी करतो.
प्रश्नसंग्रह : उदाहरण 11
एका शेतजमिनीचा आकार चौकोनी आहे. त्याच्या चार कोपऱ्यांना P, Q, R, S ही नावे दिलेली आहेत.
शेतजमिनीच्या बाजूंची लांबी पुढीलप्रमाणे आहे,
\ell\left(PQ\right)=170 मी, \ell\left(QR\right)=250 मी, \ell\left(RS\right)=100 मी, \ell\left(PS\right)=240 मी, \ell\left(PR\right)=260 मी.
या शेतजमिनीचे क्षेत्रफळ हेक्टरमध्ये काढा. ( 1 हेक्टर =10,000 चौमी)
उत्तर:
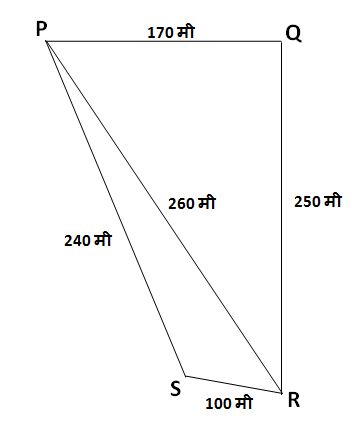
दिलेल्या शेतजमिनीच्या माहितीप्रमाणे वर काढलेल्या आकृतीत \square PQRS काढला आहे.
रेख PR हा \square PQRS चा कर्ण आहे. कर्ण PR मुळे \square PQRS ची दोन त्रिकोणांमध्ये विभागणी झालेली आहे; त्रिकोण \triangle PQR आणि \triangle PRS.
आता \square PQRS चं क्षेत्रफळ काढण्यासाठी आपल्याला ह्या दोन्ही त्रिकोणांचं क्षेत्रफळ काढून त्या क्षेत्रफळांची बेरीज करावी लागणार आहे.
आता लक्षात घ्या की ह्या दोन्ही त्रिकोणांची उंची आपल्याला माहित नाहीये; त्यामुळे आपल्याला “हेरनचं सूत्र” वापरून आपल्याला ह्या दोन त्रिकोणांचं क्षेत्रफळ काढावं लागणार आहे.
हेरनच्या सूत्राने त्रिकोणाचे क्षेत्रफळ \mathbf{A=\sqrt{s\left(s-a\right)\left(s-b\right)\left(s-c\right)}}
त्रिकोणाची परिमिती = (त्रिकोणाच्या तीन बाजूंच्या लांबीची बेरीज)
त्रिकोणाची अर्ध परिमिती s=\frac{1}{2}\times (त्रिकोणाच्या तीन बाजूंच्या लांबीची बेरीज)
\triangle PQR ची अर्ध परिमिती,
\begin{aligned} \\ &\therefore s=\frac{1}{2}\times \left(170+250+260\right) \\ &\therefore s=\frac{1}{2}\times 680 \\ &\therefore s=340\end{aligned}
\begin{aligned} \\ &A(\triangle PQR)=\sqrt{s\left(s-a\right)\left(s-b\right)\left(s-c\right)} \\ &\therefore A(\triangle PQR)=\sqrt{340\left(340-170\right)\left(340-250\right)\left(340-260\right)} \\ &\therefore A(\triangle PQR)=\sqrt{340\left(170\right)\left(90\right)\left(80\right)} \\ &\therefore A(\triangle PQR)=\sqrt{416160000} \\ &\therefore A(\triangle PQR)=20,400\end{aligned}
\triangle PRS ची अर्ध परिमिती,
\begin{aligned} \\ &\therefore s=\frac{1}{2}\times \left(100+240+260\right) \\ &\therefore s=\frac{1}{2}\times 600 \\ &\therefore s=300\end{aligned}
\begin{aligned} \\ &A(\triangle PRS)=\sqrt{s\left(s-a\right)\left(s-b\right)\left(s-c\right)} \\ &\therefore A(\triangle PRS)=\sqrt{300\left(300-100\right)\left(300-240\right)\left(300-260\right)} \\ &\therefore A(\triangle PRS)=\sqrt{300\left(200\right)\left(60\right)\left(40\right)} \\ &\therefore A(\triangle PRS)=\sqrt{144000000} \\ &\therefore A(\triangle PRS)=12,000\end{aligned}
\begin{aligned} \\ &\therefore A\left(\square PQRS\right)=A\left(PQR\right)+A\left(PRS\right) \\ &\therefore A\left(\square PQRS\right)=20,400+12,000 \\ &\therefore A\left(\square PQRS\right)=20,400+12,000 \\ &\therefore A\left(\square PQRS\right)=32,400\end{aligned}
\therefore \square ABCD चं क्षेत्रफळ 32,400 चौरस मीटर आहे.
\mathbf{\therefore \square ABCD} चं क्षेत्रफळ \mathbf{\frac{32,400}{10,000}=3.24} हेक्टर आहे.
प्रश्नसंग्रह : उदाहरण 12
एका ग्रंथालयातील एकूण पुस्तकांच्या 50% पुस्तके मराठीची आहेत. मराठीच्या पुस्तकांच्या \frac{1}{3} पुस्तके इंग्रजीची आणि इंग्रजीच्या पुस्तकांच्या 25% पुस्तके गणिताची आहेत. उरलेली 560 पुस्तके इतर विषयांची आहेत. तर त्या ग्रंथालयात एकूण किती पुस्तके आहेत?
उत्तर:
ग्रंथालयातील एकूण पुस्तकांची संख्या x मानू
\therefore मराठीच्या पुस्तकांची संख्या =x\times 50\%=\frac{1}{2}\times x=\frac{x}{2}
\therefore इंग्रजीच्या पुस्तकांची संख्या =\frac{1}{3}\times \frac{x}{2}=\frac{x}{6}
\therefore गणिताच्या पुस्तकांची संख्या =\frac{x}{6}\times 25\%=\frac{x}{6}\times \frac{1}{4}=\frac{x}{24}
\therefore समीकरण: \frac{x}{2}+\frac{x}{6}+\frac{x}{24}+560=x
आता आपण वरील समीकरण सोडवूयात,
\begin{aligned} \\ &\therefore \frac{x}{2}+\frac{x}{6}+\frac{x}{24}+560=x \\ &\therefore \frac{12x+4x+x}{24}+560=x \\ &\therefore \frac{12x+4x+x+13,440}{24}=x \\ &\therefore 24\times \frac{12x+4x+x+13,440}{24}=24\times x \\ &\therefore 12x+4x+x+13,440=24x \\ &\therefore 17x+13,440=24x \\ &\therefore 17x+13,440-17x=24x-17x \\ &\therefore 13,440=7x \\ &\therefore \frac{13,440}{7}=\frac{7x}{7} \\ &\therefore x=1920\end{aligned}
\mathbf{\therefore } त्या ग्रंथालयात एकूण 1920 पुस्तके आहेत.
प्रश्नसंग्रह : उदाहरण 13
\left(2x+1\right) या द्विपदीने \left(6x^3+11x^2-10x-7\right) या बहुपदीला भागा. भागाकार आणि बाकी लिहा.
उत्तर:
\begin{aligned} \\ \mathbf{3x^2+4x-7}\phantom{**} \\ 2x+1{\overline{\smash{\big)}6x^3+11x^2-10x-7}} \\ \underline{-6x^3-\;\,3x^2\phantom{-10x-7*}} \\ 0\phantom{**}+\;\;8x^2-10x-7 \\ \underline{-\;\;8x^2-\;\;4x\phantom{-7*}} \\ 0\phantom{**}\!-14x-7 \\ \underline{+\;14x+7} \\ \mathbf{0\phantom{**}}\end{aligned}
भागाकार =\mathbf{3x^2+4x-7} आणि बाकी =\mathbf{0}.
इयत्ता 8 वीचे पाठयपुस्तक: इथे क्लिक करा
