इयत्ता 8 वी सांख्यिकीचा उपयोग कसा करतात? : सांख्यिकी ही गणिताची एक शाखा आहे जी माहिती संकलन, विश्लेषण, स्पष्टीकरण आणि सादरीकरण यांसाठी वापरली जाते. विविध क्षेत्रांमध्ये निर्णय प्रक्रियेस मदत करण्यासाठी सांख्यिकीचा उपयोग केला जातो. संशोधन, अर्थशास्त्र, विज्ञान आणि उद्योग यांसारख्या क्षेत्रांमध्ये सांख्यिकीला महत्त्वपूर्ण स्थान आहे. आणि म्हणूनच इयत्ता 8 वी साठी सांख्यिकीचा उपयोग कसा केला जातो हे नीट समजावे म्हणून त्याचा अभ्यासक्रमात समावेश केलेला आहे.

सांख्यिकीचा उपयोग
सांख्यिकी ह्या ज्ञानशाखेत काही परिमाणासंदर्भात सांख्यिक माहिती गोळा केली जाते आणि त्या सांख्यिक माहितीचा अभ्यास करून काही निष्कर्ष काढले जातात.
(सांख्यिक माहिती म्हणजे संख्यांच्या (आकड्यांच्या) स्वरूपातील माहिती.)
सांख्यिकीमध्ये “परिमाण” म्हणजे काय?
सांख्यिकीचा उपयोग करताना परिमाण म्हणजे काय, हे सर्वप्रथम माहित असणे आवश्यक आहे.
ज्या गोष्टीबद्दल माहिती गोळा केली जाते त्याला परिमाण म्हणतात. खालील उदाहरणं बघितल्यावर हे तुमच्या लक्षात येईल,
1) देशात पडणाऱ्या “पावसाचं वार्षिक प्रमाण”, हे एक परिमाण आहे.
2) एखाद्या हंगामातील “पिकाच्या उत्पादनाचं प्रमाण”, हे एक परिमाण आहे.
3) एखाद्या शाळेच्या “10 वीच्या विद्यार्थ्यांची उत्तीर्ण होण्याची टक्केवारी”, हे एक परिमाण आहे.
सांख्यिकीचे महत्व काय?
सांख्यिकीचा उपयोग कसा केला जाऊ शकतो?
सांख्यिकीचा उपयोग अभ्यासक्रमाच्या दृष्टीने किती महत्वाचा आहे हे समजावून घेण्यासाठी आपण एक सविस्तर उदाहरण बघू, म्हणजे सांख्यिकी वापरून निष्कर्ष कसे काढले जातात, त्याची तुम्हाला कल्पना येईल.
उदाहरण:
राज्यातल्या धृतगती मार्गांवर होणाऱ्या अपघातांच्या तीव्रतेनुसार सरकारी यंत्रणेला त्या-त्या धृतगती मार्गावर काही उपाययोजना करायच्या आहेत आणि त्यासाठी त्या सरकारी यंत्रणेला गेल्या वर्षभरात त्या महामार्गांवर झालेल्या अपघातांची माहिती हवी आहे.
ही माहिती गोळा करण्यासाठी सरकारी यंत्रणा प्रत्यक्षदर्शी, पोलीस, वृत्तपत्र आणि वृत्तवाहिन्या, डॉक्टर्स आणि रुग्णालयं अशा विविध माध्यमांकडून त्या सगळ्या धृतगती मार्गांवर गेल्या वर्षभरात झालेल्या अपघातांची सांख्यिक माहिती गोळा करते आणि मिळालेल्या माहितीनुसार त्या अपघातांचे सौम्य, गंभीर आणि अतिगंभीर असं वर्गीकरण करते.
उदाहरणार्थ,
1) ज्या अपघातांमध्ये प्रवासी किरकोळ जखमी झाले आहेत किंवा वाहनांचे किरकोळ नुकसान झाले आहे, ते सौम्य अपघात.
2) ज्या अपघातांमध्ये प्रवासी गंभीर जखमी झाले आहेत किंवा वाहनांचे मोठे नुकसान झाले आहे, ते गंभीर अपघात.
3) ज्या अपघातांमध्ये प्रवासी अतीगंभीर जखमी झाले आहेत किंवा दगावले आहेत आणि वाहनांचे देखील प्रचंड नुकसान झाले आहे, ते अतीगंभीर अपघात.
आता खालील सारणीत दिल्याप्रमाणे सरकारी यंत्रणेला माहिती मिळालेली आहे आणि वर सांगितल्याप्रमाणे त्यांनी त्या माहितीचं वर्गीकरण केलेलं आहे.
| धुतगती मार्ग | एकूण अपघात | सौम्य अपघात | गंभीर अपघात | अतीगंभीर अपघात | धुतगती मार्गावर उपलब्ध करून द्यायची सेवा |
|---|---|---|---|---|---|
| धुतगती मार्ग 1 | 157 | 150 (96%) | 5 (3%) | 2 (1%) | प्रथमोपचार सेवा आणि सामान्य रुग्णवाहिका |
| धुतगती मार्ग 2 | 122 | 50 (41%) | 70 (57%) | 2 (2%) | आपत्ती निवारण पथक आणि सर्वसोईंनी सुसज्ज रुग्णवाहिका |
| धुतगती मार्ग 3 | 47 | 20 (43%) | 2 (4%) | 25 (53%) | आपत्ती निवारण पथक, सर्वसोईंनी सुसज्ज रुग्णवाहिका आणि अतिदक्षता विभाग |
| धुतगती मार्ग 4 | 115 | 50 (43%) | 25 (22%) | 40 (35%) | आपत्ती निवारण पथक, सर्वसोईंनी सुसज्ज रुग्णवाहिका आणि अतिदक्षता विभाग |
आता वरील माहितीचा कशा प्रकारे उपयोग केला गेला आणि त्याप्रमाणे सरकारी यंत्रणेने धृतगती मार्गावर कोणत्या सोयी पुरवायच्या ह्याचा निर्णय घेतला, ते पाहू,
1) धृतगती मार्ग 1 वर एकूण अपघातांपैकी सर्वात जास्त 96 टक्के अपघात हे किरकोळ स्वरूपाचे असल्याने प्रथमोपचार सेवा आणि सामान्य रुग्णवाहिकेची सेवा पुरवणं हे पुरेसं होणार आहे.
2) धृतगती मार्ग 2 वर एकूण अपघातांपैकी सर्वात जास्त 57 टक्के अपघात हे गंभीर स्वरूपाचे असल्याने आपत्ती निवारण पथक आणि सर्वसोईंनी सुसज्ज रुग्णवाहिकेची सेवा पुरवणं आवश्यक आहे.
3) धृतगती मार्ग 3 वर एकूण अपघातांपैकी सर्वात जास्त 25 टक्के अपघात हे अतीगंभीर स्वरूपाचे असल्याने आपत्ती निवारण पथक, सर्वसोईंनी सुसज्ज रुग्णवाहिका, तसेच अतिदक्षता विभागची सेवा पुरवणं आवश्यक आहे.
4) धृतगती महामार्ग 4 वर झालेल्या अपघातांची सांख्यिक माहिती बघितली असता तुमच्या लक्षात येईल की किरकोळ अपघातांचं प्रमाण सर्वात जास्त 43 टक्के जरी असलं, तरी गंभीर आणि अतीगंभीर अपघातांचं एकत्रित प्रमाण 57 टक्के असल्याने आपत्ती निवारण पथक, सर्वसोईंनी सुसज्ज रुग्णवाहिका, तसेच अतिदक्षता विभागची सेवा पुरवणं आवश्यक आहे.
ह्या उदाहरणात अपघातांची सांख्यिक माहिती अपघातांच्या प्रकारांच्या टक्केवारीत व्यक्त केल्याने निष्कर्ष काढणं सोपं झालं आहे. अशा प्रकारे सांख्यिक माहितीच्या आधारे निष्कर्ष काढले जाऊन महत्वाचे निर्णय घेतले जातात आणि त्यामुळेच सांख्यिकीचा उपयोग अत्यंत महत्वाचा आहे. पुढे आपण सांख्यिकी मधल्या काही संकल्पना शिकणार आहोत.
सांख्यिकीमध्ये “मध्य” म्हणजे काय?
सांख्यिकीचा उपयोग करताना “मध्य” ही एक महत्वाची संकल्पना आहे.
मध्य: मध्य म्हणजे सरासरी होय. सरासरी काढताना आपण (1) आधी एखाद्या गोष्टीची सांख्यिक माहिती गोळा करतो. (2) नंतर त्या संख्यांची बेरीज करतो. (3) आणि त्या बेरजेला संख्यांच्या एकूण संख्येने भागतो.
उदाहरणार्थ, एका फलंदाजाने मागील पाच डावात 25, 45, 112, 76, 88 अशा धावा केल्या असतील, तर त्या फलंदाजाची धावा करण्याची सरासरी किती होती?
1) आधी आपण त्या फलंदाजाने मागील पाच डावात केलेल्या धावांची बेरीज करून घेऊयात,
25 + 45 + 112 + 76 + 88 = 346
2) आणि त्या फलंदाजाने केलेल्या धावांची एकूण निरीक्षणं आहेत 5 (मागील 5 सामान्यात केलेल्या धावा आपण इथे विचारात घेत आहोत).
3) म्हणून त्या फलंदाची मागील पाच डावात धावा करण्याची सरासरी आहे \frac{346}{5}=69.2 धावा.
मध्य किंवा सरासरीने आपल्याला सांख्यिक माहितीचा कल कळतो. म्हणजे वरच्या उदाहरणात फलंदाजाच्या मागील पाच सामन्यात केलेल्या धावांचा मध्य किंवा सरासरी 69.2 धावा आहे. ह्या वरून आपल्या लक्षात येतं की ह्या फलंदाजाची 69 धावांच्या आसपास धावा करण्याची क्षमता आहे आणि हे लक्षात घेऊन आपण पुढील सामन्यांसाठी संघ बांधणी करू शकतो.
ह्यावरून सांख्यिकीचा उपयोग करताना “मध्य” ही किती महत्वाची संकल्पना आहे, हे तुमच्या लक्षात आलं असेल.
सांख्यिकीमध्ये “वारंवारता” म्हणजे काय?
सांख्यिकीचा उपयोग करताना “वारंवारता” ही एक महत्वाची संकल्पना आहे.
वारंवारता: सांख्यिक माहितीच्या संचामध्ये एखादी संख्या किती वेळा आली आहे, त्या संख्येला वारंवारता म्हणतात.
उदाहरणार्थ एका गोलंदाजाने गेल्या एक वर्षात खेळलेल्या प्रत्येक सामन्यात घेतलेल्या बळींची संख्या [1, 4, 3, 3, 1, 5, 2, 1, 4, 2, 1, 3, 5, 2, 1, 4] आहे. हा संख्या संच बघितल्यावर तुमच्या लक्षत येईल की ह्या संचातील संख्या एकापेक्षा जास्त वेळा संचात आलेल्या आहेत.
1) 1 ही संख्या पाच वेळा आली आहे.
2) 4 ही संख्या तीन वेळा आली आहे.
ह्या प्रमाणे एखादी संख्या संचात किती वेळा आली आहे, त्या संख्येला “वारंवारता” म्हणतात. म्हणजेच,
1) 1 ही संख्या पाच वेळा आली आहे, म्हणून 1 ह्या संख्येची वारंवारता 5 आहे.
2) 4 ही संख्या तीन वेळा आली आहे, म्हणून 4 ह्या संख्येची वारंवारता 3 आहे.
आपण ही सांख्यिक माहिती सारणीच्या स्वरूपात पुढील प्रमाणे लिहू शकतो,
| क्रिकेट सामना | मिळवलेले बळी (विकेट्स) |
|---|---|
| सामना 1 | 1 |
| सामना 2 | 4 |
| सामना 3 | 3 |
| सामना 4 | 3 |
| सामना 5 | 1 |
| सामना 6 | 5 |
| सामना 7 | 2 |
| सामना 8 | 1 |
| सामना 9 | 4 |
| सामना 10 | 2 |
| सामना 11 | 1 |
| सामना 12 | 3 |
| सामना 13 | 5 |
| सामना 14 | 2 |
| सामना 15 | 1 |
| सामना 16 | 4 |
| एकूण बळी = 42 |
| क्रिकेट सामन्यात मिळवलेले बळी (विकेट्स) | वारंवारता | बळींची संख्या = (क्रिकेट सामन्यात मिळवलेले बळी) x (वारंवारता) |
|---|---|---|
| 1 | 5 | 5 |
| 2 | 3 | 6 |
| 3 | 3 | 9 |
| 4 | 3 | 12 |
| 5 | 2 | 10 |
| एकूण वारंवारता = 16 | एकूण बळी = 42 |
मध्य (किंवा सरासरी) = एकूण बळी / एकूण वारंवारता = \frac{42}{16}=2.62
ह्यावरून सांख्यिकीचा उपयोग करताना “वारंवारता ” ही किती महत्वाची संकल्पना आहे, हे तुमच्या लक्षात आलं असेल.
सांख्यिकीमध्ये वापरले जाणारे संकेत कोणते आहेत?
संकेत: सांख्यिकीचा उपयोग करताना वापरले जाणारे काही संकेत आता आपण बघुयात,
1) आपण एखाद्या गोष्टीबद्दल जी सांख्यिक माहिती गोळा करतो, ती माहिती x (एक्स) ह्या इंग्रजी अक्षराने दर्शवली जाते.
म्हणजे वरील उदाहरणात x_i = 1, 4, 3, 3, 1, 5, 2, 1, 4, 2, 1, 3, 5, 2, 1, 4. ह्यात x_1=1, x_2=4, x_3=3 ...
2) सांख्यिक माहितीची बेरीज ही ग्रीक \mathbf{\sum} (सिग्मा) ह्या चिन्हाने दर्शवतात.
म्हणजे वरील उदाहरणात \sum{x_i}=(1+4+3+3+1+5+2+1+4+2+1+3+5+2+1+4).
3) त्याच प्रमाणे वारंवारता f (एफ) ह्या इंग्रजी अक्षराने दर्शवली जाते.
म्हणजे वरील उदाहरणात f_i = 5, 3, 3, 3, 2. ह्यात f_1=5, f_2=3, f_3=3, f_4=3, f_5=2. आणि वारंवारतेची बेरीज ही N (कॅपिटल एन) ह्या इंग्रजी अक्षराने दर्शवतात.
4) सांख्यिक माहितीचा मध्य दर्शवण्यासाठी \mathbf{\bar{x}} (एक्स बार) चा उपयोग करतात.
\mathbf{\therefore} मध्य = सांख्यिक माहितीची बेरीज / वारंवारतेची बेरीज
\therefore \mathbf{\bar{x}=\frac{\sum{f_i\times x_i}}{N}}
आता हे संकेत वापरून आपण वरील उदाहरणातील सारणी पुन्हा लिहुयात,
| क्रिकेट सामन्यात मिळवलेले बळी (विकेट्स) \mathbf{x_i} | वारंवारता \mathbf{f_i} | बळींची संख्या = (क्रिकेट सामन्यात मिळवलेले बळी) x (वारंवारता) \mathbf{f_i\times x_i} |
|---|---|---|
| 1 | 5 | 5 |
| 2 | 3 | 6 |
| 3 | 3 | 9 |
| 4 | 3 | 12 |
| 5 | 2 | 10 |
| एकूण वारंवारता \mathbf{N=16} | एकूण बळी \mathbf{\sum{f_i\times x_i}=42} |
ह्यावरून तुमच्या लक्षात आलं असेल की सांख्यिकीचा उपयोग करताना वापरले जाणारे संकेत किती महत्वाचे आहेत.
सांख्यिकीची उदाहरणे
सांख्यिकीचा उपयोग कशा प्रकारे केला जातो, हे खालील उदाहरणे सोडवल्यावर तुमच्या सहज लक्षात येईल.
उदा 1:
एका शाळेतील इयत्ता 8 वी च्या 37 विद्यार्थ्यांना गणित विषयात एका 10 गुणांच्या चाचणीत मिळालेले गुण खालीलप्रमाणे आहेत. या गुणांचा मध्य काढा.
2, 4, 4, 8, 6, 7, 3, 8, 9, 10, 10, 8, 9, 7, 6, 5, 4, 6, 7, 8, 4, 8, 9, 7, 6, 5, 10, 9, 7, 9, 10, 9, 6, 9, 9, 4, 7.
उत्तर:
आपण आधी ह्या सांख्यिक माहितीची वारंवारता सारणी तयार करून घेऊ, म्हणजे हे उदाहरण सोडवायला एकदम सोपं जाईल,
| गणित विषयात मिळवलेले गुण \mathbf{x_i} | वारंवारता \mathbf{f_i} | एकूण गुण = (गणित विषयात मिळवलेले गुण) x (वारंवारता) \mathbf{f_i\times x_i} |
|---|---|---|
| 2 | 1 | 2 |
| 3 | 1 | 3 |
| 4 | 5 | 20 |
| 5 | 2 | 10 |
| 6 | 5 | 30 |
| 7 | 6 | 42 |
| 8 | 5 | 40 |
| 9 | 8 | 72 |
| 10 | 4 | 40 |
| एकूण वारंवारता \mathbf{N=37} | एकूण गुण \mathbf{\sum{f_i\times x_i}=259} |
मध्य \bar{x}=\frac{\sum{f_i\times x_i}}{N}=\frac{259}{37}=7
गणित विषयात मिळवलेल्या गुणांचा मध्य 7 आहे.
उदा 2:
एका गावातील 30 शेतकऱ्यांचे ज्वारीचं एकरी उत्पादन क्विंटलमध्ये खालीलप्रमाणे आहे.
9, 7.5, 8, 6, 5.5, 7.5, 5, 8, 5, 6.5, 5, 5.5, 4, 4, 8, 6, 8, 7.5, 6, 9, 5.5, 7.5, 8, 5, 6.5, 5, 9, 5.5, 4, 8.
ह्या सांख्यिक माहितीवरून वारंवारता वितरण सारणी तयार करा आणि ज्वारीच्या एकरी उत्पादनाचा मध्य काढा.
उत्तर:
आपण आधी ह्या सांख्यिक माहितीची वारंवारता सारणी तयार करून घेऊ, म्हणजे हे उदाहरण सोडवायला एकदम सोपं जाईल,
| क्विंटलमध्ये ज्वारीचं एकरी उत्पादन \mathbf{x_i} | वारंवारता \mathbf{f_i} | एकूण उत्पादन = (ज्वारीचं एकरी उत्पादन) x (वारंवारता) \mathbf{f_i\times x_i} |
|---|---|---|
| 4 | 3 | 12 |
| 5 | 5 | 25 |
| 5.5 | 4 | 22 |
| 6 | 3 | 18 |
| 6.5 | 2 | 13 |
| 7.5 | 4 | 30 |
| 8 | 6 | 48 |
| 9 | 3 | 27 |
| एकूण वारंवारता \mathbf{N=30} | एकूण उत्पादन \mathbf{\sum{f_i\times x_i}=195} |
मध्य \bar{x}=\frac{\sum{f_i\times x_i}}{N}=\frac{195}{30}=6.5
एकरी सोयाबीन उत्पादनाचा मध्य 6.5 क्विंटल आहे.
उदा 3:
8 वीच्या प्रत्येक विद्यार्थ्याने लावलेल्या रोपांची संख्या खालील वारंवारता सारणीत दिली आहे; त्यावरून प्रत्येक विद्यार्थ्याने लावलेल्या रोपांचा मध्य काढा.
| रोपांची संख्या \mathbf{x_i} | वारंवारता \mathbf{f_i} |
|---|---|
| 1 | 4 |
| 2 | 6 |
| 3 | 12 |
| 4 | 8 |
उत्तर:
आधी आपण दिलेली वारंवारता सारणी पूर्ण करून घेऊ आणि रोपांची एकूण संख्या किती, ते काढू,
| रोपांची संख्या \mathbf{x_i} | वारंवारता \mathbf{f_i} | रोपांची एकूण संख्या = (रोपांची संख्या) x (वारंवारता) \mathbf{f_i\times x_i} |
|---|---|---|
| 1 | 4 | 4 |
| 2 | 6 | 12 |
| 3 | 12 | 36 |
| 4 | 8 | 32 |
| एकूण वारंवारता \mathbf{N=30} | रोपांची एकूण संख्या \mathbf{\sum{f_i\times x_i}=84} |
मध्य \bar{x}=\frac{\sum{f_i\times x_i}}{N}=\frac{84}{30}=2.8
विद्यार्थ्याने लावलेल्या रोपांचा मध्य 2.8 रोपं आहे.
उदा 4:
एका गावातील काही कुटुंबांनी मे महिन्यात वापरलेल्या वीजेच्या युनिट्सची माहिती खालील सारणीत दिलेली आहे. त्यावरून खालील प्रश्नांची उत्तर द्या.
| वीज वापर युनिट्समध्ये \mathbf{x_i} | वारंवारता \mathbf{f_i} |
|---|---|
| 30 | 7 |
| 45 | 2 |
| 60 | 8 |
| 75 | 5 |
| 90 | 3 |
1) 45 युनिट्स वीज वापरणारी एकूण किती कुटुंब आहेत?
2) ज्या प्राप्तांकाची वारंवारता ५ आहे, तो प्राप्तांक कोणता?
3) N =किती?, \sum{f_i\times x_i}=किती?
4) ह्यावरून मे महिन्यात प्रत्येक कुटुंबाने वापरलेल्या विजेच्या युनिट्सचा मध्य काढा.
उत्तर:
आधी आपण दिलेली वारंवारता सारणी पूर्ण करून घेऊ आणि विजेचा एकूण वापर किती, ते काढू,
| वीज वापर युनिट्समध्ये \mathbf{x_i} | वारंवारता \mathbf{f_i} | विजेचा एकूण वापर = (वीज वापर युनिट्समध्ये) x (वारंवारता) \mathbf{f_i\times x_i} |
|---|---|---|
| 30 | 7 | 210 |
| 45 | 2 | 90 |
| 60 | 8 | 480 |
| 75 | 5 | 375 |
| 90 | 3 | 270 |
| एकूण वारंवारता \mathbf{N=25} | विजेचा एकूण वापर \mathbf{\sum{f_i\times x_i}=1425} |
1) 45 युनिट्स वीज वापरणारी एकूण कुटुंब = 2
2) वारंवारता 5 असलेला प्राप्तांक = 75
3) N = 25 आणि \sum{f_i\times x_i=1425}
4) मध्य \bar{x}=\frac{\sum{f_i\times x_i}}{N}=\frac{1425}{25}=57
मे महिन्यात प्रत्येक कुटुंबाने वापरलेल्या विजेच्या युनिट्सचा मध्य 57 आहे.
उदा 5:
एक गावातील 40 कुटुंबांतील सदस्यांची संख्या पुढीलप्रमाणे आहे.
1, 6, 5, 4, 3, 2, 7, 2, 3, 4, 5, 6, 4, 6, 2, 3, 2, 1, 4, 5, 6, 7, 3, 4, 5, 2, 4, 3, 2, 3, 5, 5, 4, 6, 2, 3, 5, 6, 4, 2.
ह्या वरून ह्या 40 कुटुंबांतील सदस्यांचा मध्य वारंवारता सारणीचा वापर करून काढा.
उत्तर:
आपण आधी ह्या सांख्यिक माहितीची वारंवारता सारणी तयार करून घेऊ, म्हणजे हे उदाहरण सोडवायला एकदम सोपं जाईल,
| सदस्यांची संख्या \mathbf{x_i} | वारंवारता \mathbf{f_i} | सदस्यांची एकूण संख्या = (सदस्यांची संख्या) x (वारंवारता) \mathbf{f_i\times x_i} |
|---|---|---|
| 1 | 2 | 2 |
| 2 | 8 | 16 |
| 3 | 7 | 21 |
| 4 | 8 | 32 |
| 5 | 7 | 35 |
| 6 | 6 | 36 |
| 7 | 2 | 14 |
| एकूण वारंवारता \mathbf{N=40} | सदस्यांची एकूण संख्या \mathbf{\sum{f_i\times x_i}=156} |
मध्य \bar{x}=\frac{\sum{f_i\times x_i}}{N}=\frac{156}{40}=3.9
कुटुंबांतील सदस्यांचा मध्य 3.9 आहे.
उदा 6:
एका शाळेने राज्यस्तरीय विज्ञान प्रदर्शनात मागील 20 वर्षांत सादर केलेल्या विज्ञान आणि गणित प्रकल्पांची संख्या खालीलप्रमाणे आहे. या वरून वारंवारता सारणी तयार करून सामग्रीचा मध्य काढा.
2, 3, 4, 1, 2, 3, 1, 5, 4, 2, 3, 1, 3, 5, 4, 3, 2, 2, 3, 2.
उत्तर:
आपण आधी ह्या सांख्यिक माहितीची वारंवारता सारणी तयार करून घेऊ, म्हणजे हे उदाहरण सोडवायला एकदम सोपं जाईल,
| प्रकल्पांची संख्या \mathbf{x_i} | वारंवारता \mathbf{f_i} | प्रकल्पांची एकूण संख्या = (प्रकल्पांची संख्या) x (वारंवारता) \mathbf{f_i\times x_i} |
|---|---|---|
| 1 | 3 | 3 |
| 2 | 6 | 12 |
| 3 | 6 | 18 |
| 4 | 3 | 12 |
| 5 | 2 | 10 |
| एकूण वारंवारता \mathbf{N=20} | प्रकल्पांची एकूण संख्या \mathbf{\sum{f_i\times x_i}=55} |
मध्य \bar{x}=\frac{\sum{f_i\times x_i}}{N}=\frac{55}{20}=2.75
प्रकल्पांच्या संख्येचा मध्य 2.75 आहे.
सांख्यिकीमध्ये आलेखाचा उपयोग
सांख्यिकीचा उपयोग करताना आलेखाचा उपयोग कसा केला जातो, हे आता आपण समजावून घेऊयात.
आलेख म्हणजे काय?
आलेख म्हणजे सांख्यिक माहिती चित्र स्वरूपात दर्शविण्याची पद्धत आहे.
माहिती चित्र स्वरूपात का दर्शवतात?
एखादी माहिती जेंव्हा चित्र स्वरूपात दर्शवली जाते, तेंव्हा बघणाऱ्याला ती अधिक सोप्या रीतीने पटकन लक्षात येते. उदाहरणार्थ वाहतूक विभागाने रस्त्यावरील वाहतूक नियंत्रित करण्यासाठी लावलेल्या अनेक प्रकारच्या पाट्या; ह्या पाट्यांवर खालील चित्रात दाखवल्याप्रमाणे चालकाला निर्देश देण्यासाठी फक्त काही चिन्ह दर्शवलेली असतात. ती चिन्ह पाहून वेगात वाहन चालवणाऱ्या चालकाला आपण काय कृती करायला पाहिजे, हे चटकन लक्षात येते. हीच माहिती जर शब्दांच्या स्वरूपात दर्शवली असती तर वेगात वाहन चालवणाऱ्या चालकाला ते निर्देश वाचताच आले नसते आणि अपघात घडण्याची शक्यता वाढली असती.

आलेखामुळे काय फायदे होतात?
वर सांगितल्याप्रमाणे आलेख म्हणजे चित्र स्वरूपात दर्शवलेली सांख्यिक माहिती असते.
1) आलेख बघणाऱ्याला सांख्यिक माहिती चटकन लक्षात येते.
2) आलेख बघितल्यावर सविस्तर सांख्यिक माहिती बघायची गरज भासत नाही.
3) आलेखावरून सांख्यिक माहितीचा कल लक्षात येतो.
4) त्याच प्रमाणे आलेख पाहून आपण सांख्यिक माहितीच्या दोन किंवा अधिक संचांची तुलना करू शकतो.
एक काल्पनिक सांख्यिक माहितीचा संच घेऊन आपण आलेखाचं महत्व समजावून घेऊ,
खालील सारणीत एका शाळेने गेल्या 20 वर्षात जिंकलेल्या वार्षिक पुरस्कारांची सांख्यिक माहिती दिलेली आहे. आणि त्याखाली आपण ही माहिती आलेखाच्या स्वरूपात दाखवलेली आहे. X अक्षावर वर्ष आणि Y अक्षावर जिंकलेल्या पुरस्कारांची संख्या दर्शवली आहे.
| वर्ष | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 | 2023 |
| शाळेने जिंकलेले एकूण वार्षिक पुरस्कार | 2 | 1 | 5 | 2 | 2 | 1 | 3 | 3 | 2 | 1 | 1 | 0 | 5 | 3 | 6 | 4 | 3 | 4 | 3 | 3 |
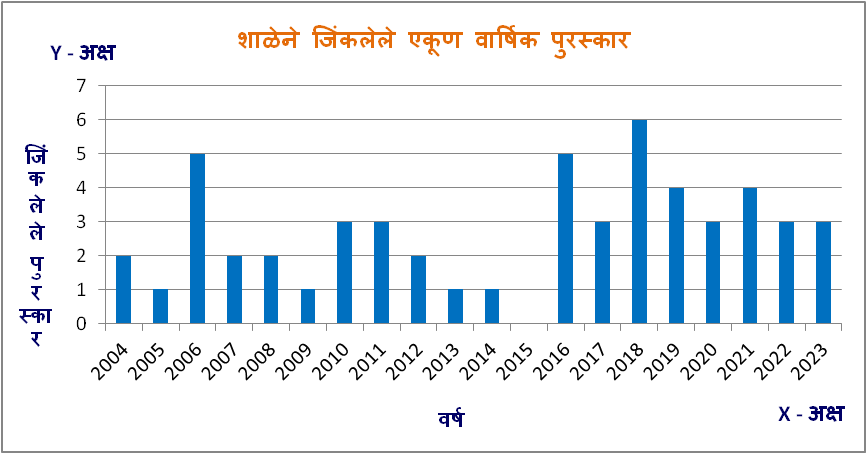
आता जर तुम्हाला कोणी विचारलं की कोणत्या वर्षी शाळेने सर्वात जास्त वार्षिक पुरस्कार जिंकले; तर त्याचं उत्तर देण्यासाठी प्रथम तुम्ही सारणी बघून उत्तर द्या आणि नंतर आलेख बघून उत्तर द्या. आणि आता तुमचं निरीक्षण नोंदवा की कोणत्या पद्धतीने उत्तर द्यायला कमी वेळ लागला; सारणी वापरून की आलेख वापरून.
आलेखातील सर्वात उंच स्तंभ शाळेने जिंकलेले सर्वात जास्त पुरस्कार दर्शवतो. उत्तर आहे 2018, ज्या वर्षी शाळेने 6 पुरस्कार जिंकलेले आहेत.
ह्या वरून तुमच्या सहज लक्षात येईल की आलेख वापरून उत्तर द्यायला खूपच कमी वेळ लागतो.
आता सराव म्हणून खालील प्रश्नांची उत्तरं तुम्ही सारणी आणि आलेख वापरून शोधा आणि कोणत्या पद्धतीने उत्तर शोधायला जास्त सोपं जातं, त्याची निरीक्षणं नोंदवा,
1) कोणत्या वर्षी शाळेला एकही पुरस्कार मिळाला नाही?
2) कोणत्या वर्षी शाळेला 2 पुरस्कार मिळाले?
3) 2023 वर्षांपासून मागील पाच वर्षांचा विचार करता, पुढील 2024 मध्ये शाळेला किती पुरस्कार मिळण्याची शक्यता आहे? म्हणजे सांख्यिक माहितीचा कल काय सांगतो?
वरील उदाहरणात आपण फक्त 20 संख्यांचा अभ्यास केला; पण जर आपल्याला 20 हजार संख्यांच्या संचाचा अभ्यास करायचा असेल तर कितीतरी अधिक वेळ खर्च करायला लागेल. अशा वेळी अशा मोठ्या संख्या संचाचा आलेख काढला तर आपला बराच वेळ वाचतो आणि सर्वात महत्वाचं म्हणजे, नुसता आलेख बघून आपल्या अनेक प्रश्नांची उत्तरं सहज मिळतात.
आलेख म्हणजे काय आणि त्याचा कसा उपयोग केला जातो, हे तुमच्या आता लक्षात आले असेल.
वर चर्चा केलेल्या उदाहरवरून सांख्यिकीचा उपयोग करताना आलेखाचा उपयोग कसा केला जातो, हे तुमच्या लक्षात आलं असेल.
विभाजित स्तंभालेख
सांख्यिकीचा उपयोग करताना विभाजित स्तंभालेखाचा उपयोग कसा केला जातो, हे आता आपण समजावून घेऊयात.
विभाजित स्तंभालेख शिकण्याआधी आपण जोड स्तंभालेख कसा असतो ते पाहू, म्हणजे तुम्हाला विभाजित स्तंभालेख समजायला सोपा जाईल.
दोन संख्या संचांचं तुलनात्मक विश्लेषण करण्यासाठी खालील प्रमाणे जोड स्तंभालेखाचा उपयोग केला जातो.
खालील जोड स्तंभालेखात दोन संघांनी 20-ट्वेंटी क्रिकेट सामन्यात प्रत्येक ओव्हरमध्ये केलेल्या धावांची तुलना केलेली आहे. लाल रंगाचे स्तंभ संघ 1 ने केलेल्या धावा दर्शवत आहेत, तर निळ्या रंगाचे स्तंभ संघ 2 ने केलेल्या धावा दर्शवत आहेत.
| ओव्हर्स | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| संघ 1 | 9 | 5 | 2 | 10 | 8 | 5 | 10 | 7 | 3 | 8 | 11 | 9 | 2 | 8 | 12 | 15 | 9 | 11 | 8 | 11 |
| संघ 2 | 10 | 8 | 5 | 9 | 12 | 10 | 8 | 6 | 9 | 6 | 9 | 8 | 6 | 5 | 10 | 10 | 6 | 7 | 9 | 8 |
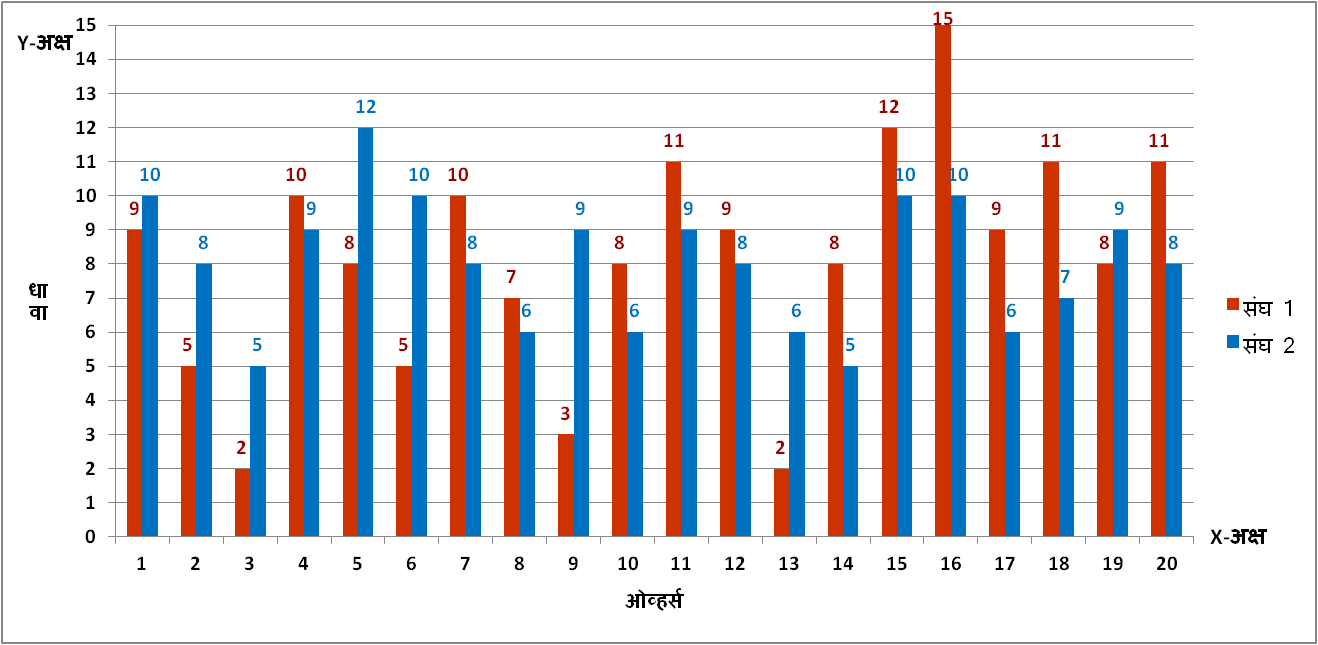
वर तयार केलेला जोड स्तंभालेख बघून आपण सहज सांगू शकतो की पहिल्या पाच ओव्हर्समध्ये संघ 2 ने संघ 1 पेक्षा जास्त धावा केलेल्या आहेत, तर शेवटच्या पाच ओव्हर्समध्ये संघ 1 ने संघ 2 पेक्षा जास्त धावा केलेल्या आहेत. त्याचप्रमाणे मधल्या 10 ओव्हर्समध्ये दोन्ही संघांनी साधारण सारख्याच धावा केलेल्या आहेत.
अशा प्रकारे जोड स्तंभालेख वापरून एकापेक्षा अधिक संख्या संचांचा तुलनात्मक अभ्यास सोप्या पद्धतीने करता येतो.
आता आपण विभाजित स्तंभालेख म्हणजे काय ते पाहू. विभाजित स्तंभालेख हे जोड स्तंभालेखाचेच एक रूप आहे. जोड स्तंभलेखात दोन किंवा अधिक परिमाणांचे स्तंभ एकमेकांशेजारी दर्शवले जातात, तर विभाजित स्तंभालेखात ते एकाच स्तंभात एकावर एक अशा पद्धतीने दर्शवले जातात.
आता आपण वरील क्रिकेट सामन्याचं उदाहरण विभाजित स्तंभालेख वापरून कसं दर्शवतात, ते पाहू,
| ओव्हर्स | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| संघ 1 | 9 | 5 | 2 | 10 | 8 | 5 | 10 | 7 | 3 | 8 | 11 | 9 | 2 | 8 | 12 | 15 | 9 | 11 | 8 | 11 |
| संघ 2 | 10 | 8 | 5 | 9 | 12 | 10 | 8 | 6 | 9 | 6 | 9 | 8 | 6 | 5 | 10 | 10 | 6 | 7 | 9 | 8 |

आपण आता विभाजित स्तंभालेख कसा वाचायचा ते बघू,
1) संघ 1 ने पहिल्या ओव्हरमध्ये 9 धावा केलेल्या आहेत. त्या धावा आपण विभाजित स्तंभालेखात पहिल्या स्तंभात खालच्या भागात 0 ते 9 अशा 9 घरांनी लाल रंगाने दर्शविल्या आहेत.
2) त्याच प्रमाणे संघ 2 ने पहिल्या ओव्हरमध्ये केलेल्या 10 धावा, विभाजित स्तंभालेखात पहिल्याच स्तंभात वरच्या भागात 9 ते 19 अशा 10 घरांनी नीळ्या रंगाने दर्शविल्या आहेत.
3) म्हणजे आपण दोन्ही संघांनी एकाच ओव्हरमध्ये केलेल्या धावा विभाजित स्तंभालेखात एकाच स्तंभात वर-खाली अशा रचनेत दाखवलेल्या आहेत.
ह्यावरून तुमच्या लक्षात आलं असेल की सांख्यिकीचा उपयोग करताना विभाजित स्तंभालेखात केल्या जाणाऱ्या सांख्यिक माहितीच्या वर-खाली रचनेमुळे सांख्यिक माहितीचं तुलनात्मक विश्लेषण करणं अधिक सोपं जातं.
आता आपण काही उदाहरणं सोडवू, म्हणजे तुम्हाला सांख्यिकीचा उपयोग करताना विभाजित स्तंभालेखाचा उपयोग कसा केला जातो, ते अधिक चांगल्याप्रकारे लक्षात येईल.
उदाहरणं
खालील उदाहरणे सोडवल्यावर सांख्यिकीचा उपयोग करताना विभाजित स्तंभालेखाचा उपयोग कसा केला जातो, हे अधिक स्पष्ट होईल.
उदा: 1
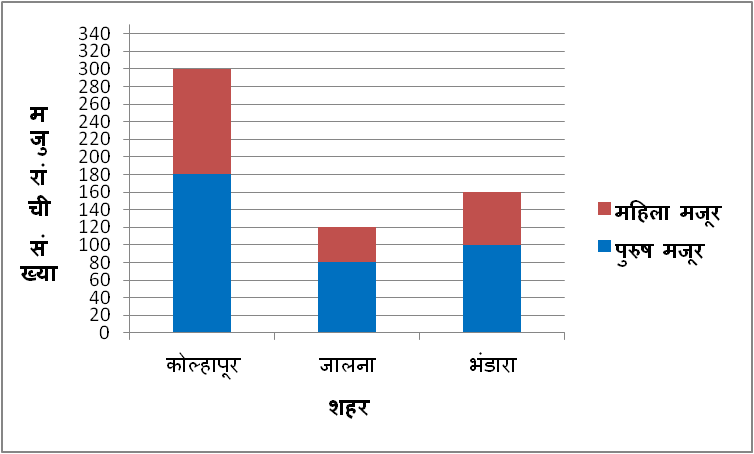
खालील सारणीत दिलेली सांख्यिक माहिती विभाजित स्तंभालेख स्वरूपात दर्शवा.
| शहर | कोल्हापूर | जालना | भंडारा |
| पुरुष मजूर | 180 | 80 | 100 |
| महिला मजूर | 120 | 40 | 60 |
उत्तर:
1) विभाजित स्तंभालेख तयार करताना आपण X-अक्षावर शहरं आणि Y-अक्षावर मजुरांची संख्या घेतलेली आहे.
2) Y-अक्षावरील प्रमाण घेताना मजुरांच्या संख्येच्या 20 च्या पटीत प्रमाण घेतलेले आहे (म्हणजेच आलेख कागदावर 1 सेमी = 20 मजूर असं प्रमाण तुम्ही घेऊ शकता).
3) पहिल्या स्तंभात कोल्हापूर शहरातील मजुरांची संख्या दर्शवली आहे. स्तंभाच्या खालच्या भागात पुरुष मजुरांची 180 ही संख्या 0 ते 180 घरांनी निळ्या रंगाने दर्शवली आहे. त्याच प्रमाणे स्तंभाच्या वरच्या भागात महिला मजुरांची 120 ही संख्या 180 ते 300 घरांनी लाल रंगाने दर्शवली आहे.
4) कोल्हापूर प्रमाणेच जालना आणि भंडारा शहरांमधील पुरुष आणि महिला मजुरांची संख्या इतर दोन स्तंभांमध्ये दर्शवली आहे.
अशा प्रकारे आपण दोन किंवा अधिक परिमाणांची दिलेली सांख्यिक माहिती विभाजित स्तंभालेखात दर्शवू शकतो.
उदा: 2
खालील आकृतीवरून खाली दिलेल्या प्रश्नांची उत्तरं द्या.

उत्तर:
1) वरील आकृती कोणत्या प्रकारच्या स्तंभालेखाची आहे?
उत्तर: वरील आकृती विभाजित स्तंभालेखाची आहे.
2) वर्षाची एप्रिल महिन्यातली बचत किती आहे?
उत्तर: 600 रुपये.
3) मिनलची मार्च आणि एप्रिल महिन्यांतली एकूण बचत किती?
उत्तर: 800 रुपये.
4) सविताची एकूण बचत श्राद्धाच्या एकूण बचतीपेक्षा किती जास्त आहे?
उत्तर: 500 रुपये.
5) कोणाची एप्रिल महिन्यातील बचत सर्वांत कमी आहे?
उत्तर: श्रद्धा.
उदा: 3
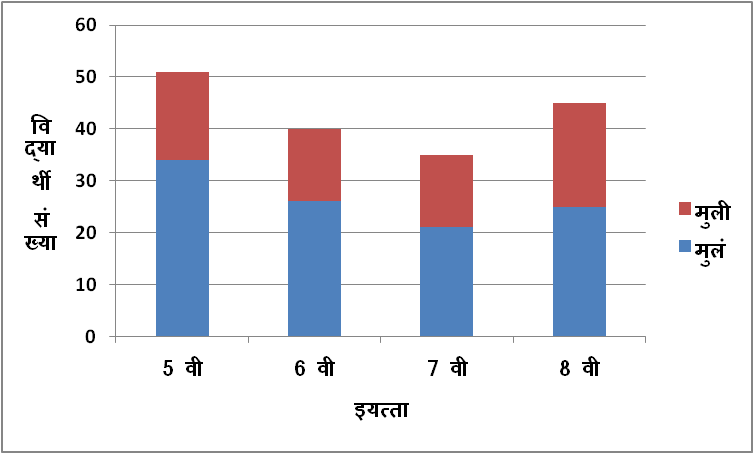
खालील सारणीत एक शाळेतील ५वि ते ८वी च्या विद्यार्थ्यांची माहिती दिलेली आहे; त्यावरून विभाजित स्तंभालेख काढा.
| 5 वी | 6 वी | 7 वी | 8 वी | |
| मुलं | 34 | 26 | 21 | 25 |
| मुली | 17 | 14 | 14 | 20 |
उत्तर:
1) विभाजित स्तंभालेख काढण्यासाठी Y-अक्षावर 1 सेमी = 10 विद्यार्थी हे प्रमाण घेतले आहे.
2) स्तंभालेखात स्तंभांचा निळ्या रंगाचा भाग मुलं, तर लाल रंगाचा भाग मुलींची संख्या दर्शवत आहे.
उदा: 4
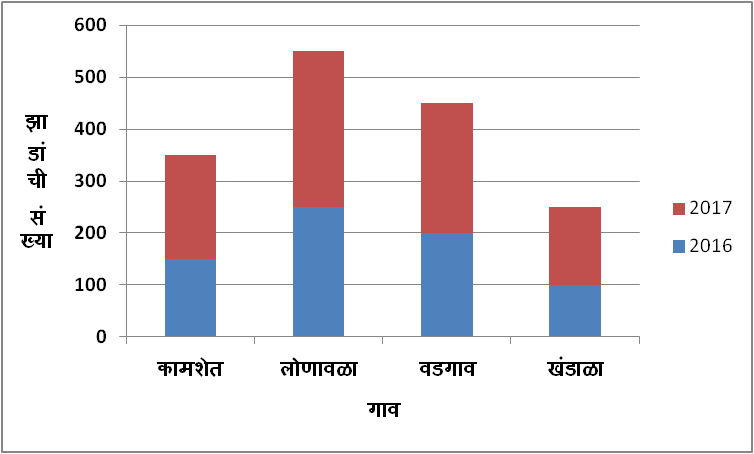
खालील सारणीत वेगवेगळ्या गावांमध्ये 2016 आणि 2017 ह्या वर्षांत लावलेल्या झाडांची संख्या दिलेली आहे. सारणीतील माहिती विभाजित स्तंभालेखात दाखवा.
| कामशेत | लोणावळा | वडगाव | खंडाळा | |
| 2016 | 150 | 250 | 200 | 100 |
| 2017 | 200 | 300 | 250 | 150 |
उत्तर:
1) विभाजित स्तंभालेख काढण्यासाठी Y-अक्षावर 1 सेमी = 100 झाडं, हे प्रमाण घेतले आहे.
2) स्तंभालेखात स्तंभांचा निळ्या रंगाचा भाग 2016 मध्ये, तर लाल रंगाचा भाग 2017 मध्ये लावलेली झाडं दर्शवत आहे.
उदा: 5
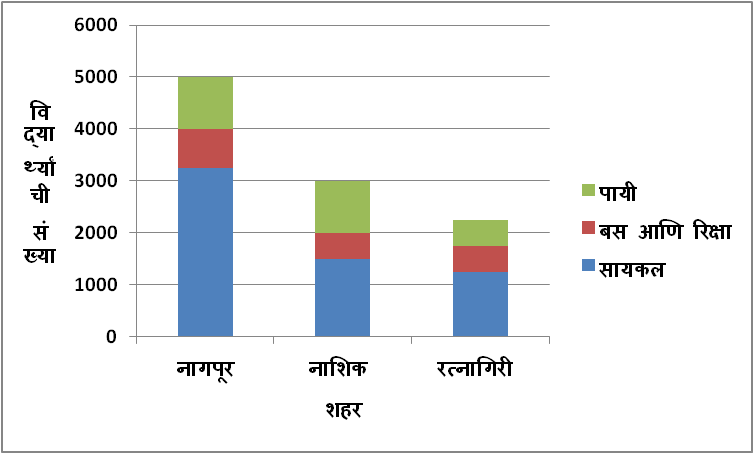
खालील सारणीत तीन शहरांतील 9 वीच्या विद्यार्थ्यांनी शाळेत जाण्यासाठी वापरलेल्या वाहतुकीच्या साधनांची व पायी जाणाऱ्यांची माहिती दिली आहे. ही माहिती दर्शवणारा विभाजित स्तंभालेख काढा.
| नागपूर | नाशिक | रत्नागिरी | |
| सायकल | 3250 | 1500 | 1250 |
| बस आणि रिक्षा | 750 | 500 | 500 |
| पायी | 1000 | 1000 | 500 |
उत्तर:
1) विभाजित स्तंभालेख काढण्यासाठी Y-अक्षावर 1 सेमी = 1000 विद्यार्थी, हे प्रमाण घेतले आहे.
2) स्तंभालेखात स्तंभांचा निळ्या रंगाचा भाग सायकलवरून शाळेत येणाऱ्या विद्यार्थ्यांचं प्रमाण, लाल रंगाचा भाग बस आणि रिक्षाने शाळेत येणाऱ्या विद्यार्थ्यांचं प्रमाण, तर हिरव्या रंगाचा भाग पायी शाळेत येणाऱ्या विद्यार्थ्यांचं प्रमाण दर्शवत आहे.
शतमान विभाजित स्तंभालेख
सांख्यिकीचा उपयोग करताना शतमान विभाजित स्तंभालेखाचा उपयोग कसा केला जातो, हे आता आपण समजावून घेऊयात.
शतमान विभाजित स्तंभालेख सांख्यिक माहितीची टक्केवारी दर्शवतो; त्यामुळे शतमान विभाजित स्तंभलेखामध्ये प्रत्येक स्तंभ हा 100 घरांचा (म्हणजे 100 टक्क्यांचा असतो) आणि सांख्यिक माहितीची टक्केवारी वेगळ्या रंगाने किंवा खुणेने दर्शवली जाते. खालील उदाहरणावरून आपण ते समजावून घेऊ,
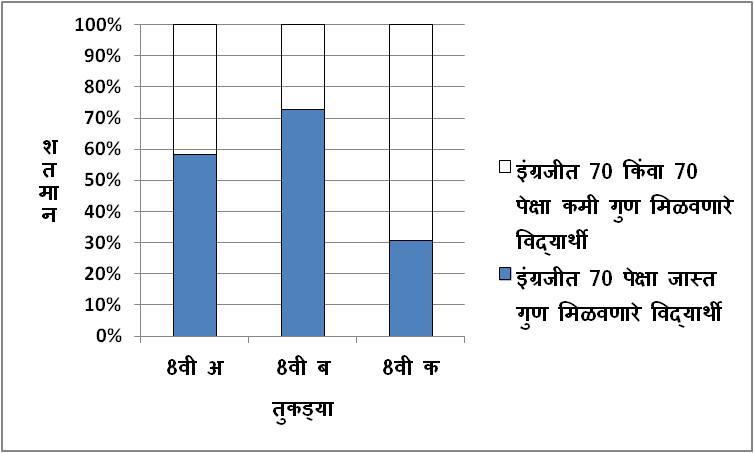
उदाहरण: एका शाळेतील 8वी च्या इंग्रजीच्या परीक्षेत 70 पेक्षा अधिक गुण मिळवणाऱ्या तीन तुकड्यांमधील विद्यार्थ्यांचं प्रमाण खालील सारणीत दिलेले आहे. त्यावरून विभाजित स्तंभालेख काढा.
| 8वी अ | 8वी ब | 8वी क | |
| इंग्रजीत 70 पेक्षा जास्त गुण मिळवणारे विद्यार्थी | 35 | 40 | 20 |
| एकूण विद्यार्थी | 60 | 55 | 65 |
उत्तर:
1) शतमान विभाजित स्तंभालेख काढण्यासाठी Y-अक्षावर 1 सेमी = 10%, हे प्रमाण घेतले आहे.
2) दिलेल्या सांख्यिक माहितीवरून आपण खालील प्रमाणे 8वीच्या प्रत्येक तुकडीचं इंग्रजीतल्या गुणांचं शतमान काढू आणि त्याप्रमाणे शतमान विभाजित स्तंभालेख काढू,
| 8वी अ | 8वी ब | 8वी क | |
| इंग्रजीत 70 पेक्षा जास्त गुण मिळवणारे विद्यार्थी | 35 | 40 | 20 |
| एकूण विद्यार्थी | 60 | 55 | 65 |
| इंग्रजीत 70 पेक्षा जास्त गुण मिळवणाऱ्या विद्यार्थ्यांचं शतमान | \mathbf{\left(\frac{35}{60}\times 100\right)=58\%} | \mathbf{\left(\frac{40}{55}\times 100\right)=73\%} | \mathbf{\left(\frac{20}{65}\times 100\right)=31\%} |
उदाहरणं
आता आपण काही उदाहरणं सोडवू, म्हणजे तुम्हाला सांख्यिकीचा उपयोग करताना शतमान विभाजित स्तंभालेखाचा उपयोग कसा केला जातो, ते अधिक चांगल्याप्रकारे लक्षात येईल.
उदा 1:
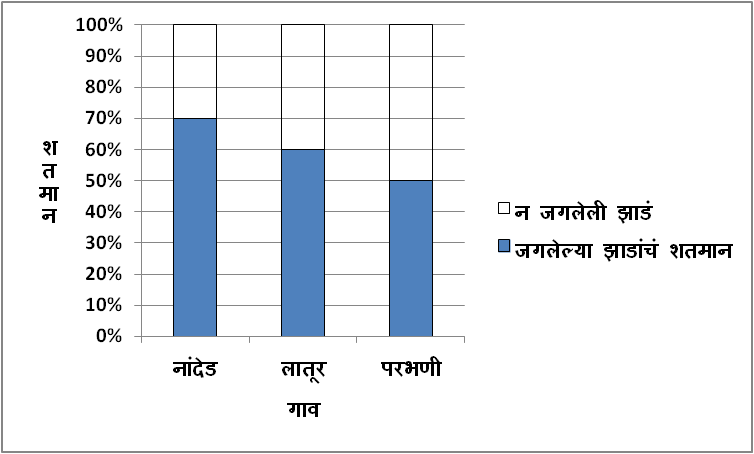
खालील सारणीत काही गावांमध्ये लागवड केलेल्या आणि त्यापैकी जगलेल्या झाडांची सांख्यिक माहिती दिलेली आहे; त्यावरून जगलेल्या झाडांचे प्रमाण, शतमान विभाजित स्तंभालेखात दाखवा.
| नांदेड | लातूर | परभणी | |
| लावलेली एकूण झाडं | 60 | 75 | 90 |
| जगलेली झाडं | 42 | 45 | 45 |
उत्तर:
1) शतमान विभाजित स्तंभालेख काढण्यासाठी Y-अक्षावर 1 सेमी = 10%, हे प्रमाण घेतले आहे.
2) दिलेल्या सांख्यिक माहितीवरून आपण खालील प्रमाणे जगलेल्या झाडांचं शतमान काढू आणि त्याप्रमाणे शतमान विभाजित स्तंभालेख काढू,
| नांदेड | लातूर | परभणी | |
| लावलेली एकूण झाडं | 60 | 75 | 90 |
| जगलेली झाडं | 42 | 45 | 45 |
| जगलेल्या झाडांचं शतमान | \mathbf{\left(\frac{42}{60}\times 100=70\%\right)} | \mathbf{\left(\frac{45}{75}\times 100=60\%\right)} | \mathbf{\left(\frac{45}{90}\times 100=50\%\right)} |
उदा 2:
गणिताच्या परीक्षेत A श्रेणी मिळवलेल्या ८वीच्या वेगवेगळ्या तुकड्यांमधील विद्यार्थ्यांची सांख्यिक माहिती दिलेली आहे; त्यावरून विभाजित स्तंभालेख काढा.
| A | B | C | D | |
| गणिताच्या परीक्षेत A श्रेणीमध्ये आलेले विद्यार्थी | 45 | 33 | 10 | 15 |
| एकूण विद्यार्थी | 60 | 55 | 40 | 75 |
उत्तर:
1) शतमान विभाजित स्तंभालेख काढण्यासाठी Y-अक्षावर 1 सेमी = 10%, हे प्रमाण घेतले आहे.
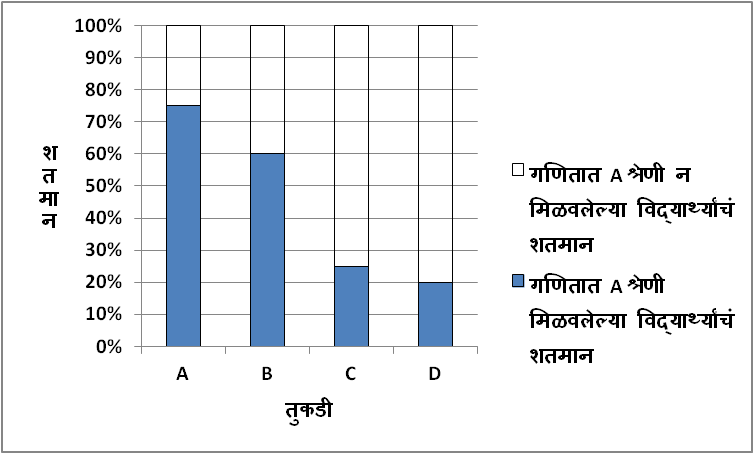
2) दिलेल्या सांख्यिक माहितीवरून आपण खालील प्रमाणे गणिताच्या परीक्षेत A श्रेणी मिळवलेल्या विद्यार्थ्यांचं शतमान काढू आणि त्याप्रमाणे शतमान विभाजित स्तंभालेख काढू,
| A | B | C | D | |
| गणिताच्या परीक्षेत A श्रेणीमध्ये आलेले विद्यार्थी | 45 | 33 | 10 | 15 |
| एकूण विद्यार्थी | 60 | 55 | 40 | 75 |
| A श्रेणी मिळवलेल्या विद्यार्थ्यांचं शतमान | \left(\frac{45}{60}\times 100=75\%\right) | \left(\frac{33}{55}\times 100=60\%\right) | \left(\frac{10}{40}\times 100=25\%\right) | \left(\frac{15}{75}\times 100=20\%\right) |
उदा 3:
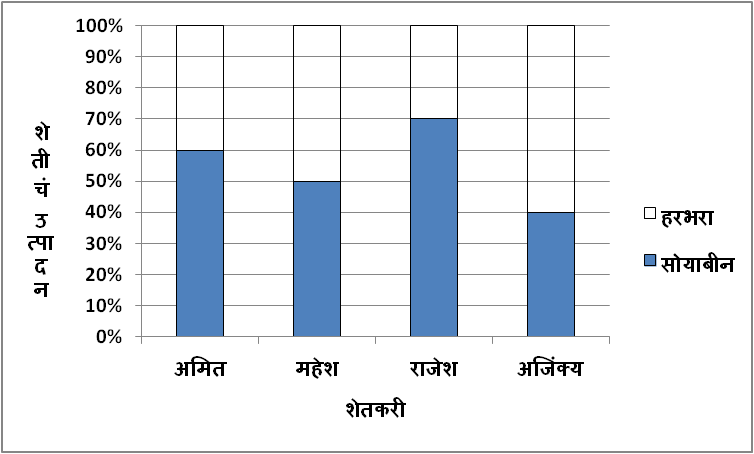
दिलेल्या स्तंभालेखाचं निरीक्षण करून खालील प्रश्नांची उत्तरं द्या.
उत्तर:
1) दिलेला स्तंभालेख कोणत्या प्रकारचा आहे?
उत्तर: शतमान विभाजित स्तंभालेख.
2) अमितच्या शेतातील सोयाबीनचं उत्पादन एकूण उत्पादनाच्या किती टक्के आहे?
उत्तर: 60%
3) महेश आणि राजेश यांच्या हरभरा उत्पादनापैकी कोणाचे शतमान उत्पादन कितीने जास्त आहे?
उत्तर: महेशचे हरभऱ्याचे उत्पादन 20 टक्क्यांनी जास्त आहे.
4) सोयाबीनच्या उत्पादनाचे सर्वांत कमी शतमान कोणाचे आहे?
उत्तर: अजिंक्यचे.
5) अजिंक्यच्या सोयाबीन आणि हरभरा यांच्या उत्पादनांची शेकडेवारी किती?
उत्तर: सोयाबीन 40% आणि हरभरा 60%.
उदा 4:
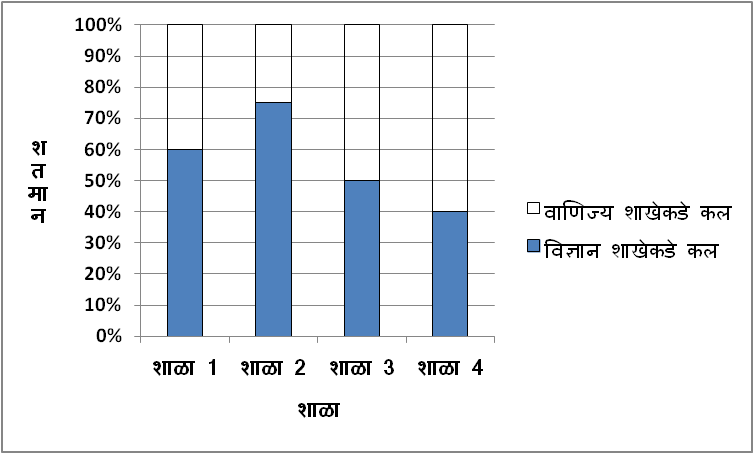
चार शाळांतील इयत्ता 10 वीतील विद्यार्थ्यांचा कल कोणत्या शाखेकडे आहे, ह्याचं सर्वेक्षण करून मिळालेली सांख्यिक माहिती खालील सारणीत दिली आहे. ती माहिती शतमान स्तंभालेखाने दाखवा.
| शाळा 1 | शाळा 2 | शाळा 3 | शाळा 4 | |
| विज्ञान शाखेकडे कल असणारे विद्यार्थी | 90 | 60 | 25 | 16 |
| वाणिज्य शाखेकडे कल असणारे विद्यार्थी | 60 | 20 | 25 | 24 |
| एकूण विद्यार्थी | 150 | 80 | 50 | 40 |
उत्तर:
1) शतमान विभाजित स्तंभालेख काढण्यासाठी Y-अक्षावर 1 सेमी = 10%, हे प्रमाण घेतले आहे.
2) दिलेल्या सांख्यिक माहितीवरून खालील प्रमाणे आपण विज्ञान शाखेकडे कल असणाऱ्या आणि वाणिज्य शाखेकडे कल असणाऱ्या विद्यार्थ्यांच्या संख्येचं शतमान काढू आणि त्याप्रमाणे शतमान विभाजित स्तंभालेख काढू,
| शाळा 1 | शाळा 2 | शाळा 3 | शाळा 4 | |
| विज्ञान शाखेकडे कल असणारे विद्यार्थी | 90 | 60 | 25 | 16 |
| वाणिज्य शाखेकडे कल असणारे विद्यार्थी | 60 | 20 | 25 | 24 |
| एकूण विद्यार्थी | 150 | 80 | 50 | 40 |
| विज्ञान शाखेकडे कल असणाऱ्या विद्यार्थ्यांचं शतमान | \mathbf{\left(\frac{90}{150}\times 100\right)=60\%} | \mathbf{\left(\frac{60}{80}\times 100\right)=75\%} | \mathbf{\left(\frac{25}{50}\times 100\right)=50\%} | \mathbf{\left(\frac{16}{40}\times 100\right)=40\%} |
| वाणिज्य शाखेकडे कल असणाऱ्या विद्यार्थ्यांचं शतमान | \mathbf{\left(\frac{60}{150}\times 100\right)=40\%} | \mathbf{\left(\frac{20}{80}\times 100\right)=25\%} | \mathbf{\left(\frac{25}{50}\times 100\right)=50\%} | \mathbf{\left(\frac{24}{40}\times 100\right)=60\%} |
इयत्ता 8 वी गणित पाठ्यपुस्तक: इथे क्लिक करा
