इयत्ता 8 वी पृष्ठफळ व घनफळ म्हणजे काय? : एखाद्या वस्तूच्या पृष्ठभागाच्या एकूण क्षेत्रफळाला त्या वस्तूचे “पृष्ठफळ” म्हणतात आणि वस्तूच्या पदार्थ घेण्याच्या क्षमतेला त्या वास्तूचे “घनफळ” म्हणतात.

पृष्ठफळ म्हणजे काय?
पृष्ठफळ व घनफळ यांची ओळख करून घेताना आपण आधी पृष्ठफळ म्हणजे काय ते पाहू,
समजा आपल्याकडे एक पुठ्याचं चौकोनी खोकं (बॉक्स) आहे. चौकोनी खोक्याला एकूण 6 पृष्ठभाग असतात; चार दिशांना चार आणि एक वर आणि एक खाली. जेंव्हा आपण ह्या 6 पृष्ठभागांचं एकूण क्षेत्रफळ काढतो, तेंव्हा त्याला त्या खोक्याचं पृष्ठफळ असं म्हणतात. एक महत्वाची बाब लक्षात घ्या की इथे आपण त्या खोक्याचा फक्त पृष्ठभाग विचारात घेतलेला आहे.
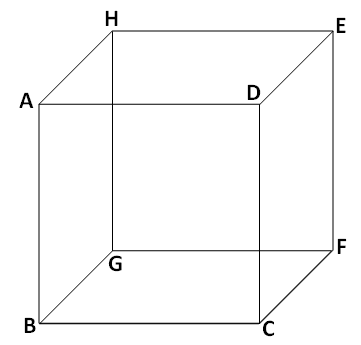
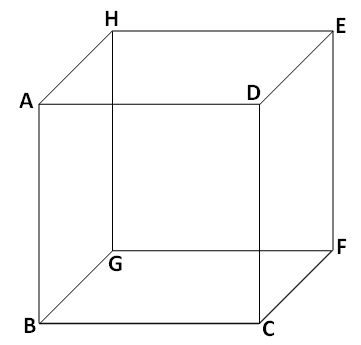
शेजारील आकृतीत आपल्याला एक चौकोनी खोकं (बॉक्स) दिलेलं आहे.
ह्या खोक्याला पुढील 6 पृष्ठभाग आहेत,
(1)\; \square ABCD
(2)\; \square CDEF
(3)\; \square EFGH
(4)\; \square ABGH
(5)\; \square ADEH
(6)\; \square BCFG
ह्या प्रत्येक पृष्ठभागाच्या प्रत्येक बाजूची लांबी 1 मीटर आहे. ह्याचा अर्थ हा प्रत्येक पृष्ठभाग हा चौरस आहे.
\therefore \square ABCD चं क्षेत्रफळ =(एका बाजूची लांबी)^2
\begin{aligned} \\ &\therefore A\left(\square ABCD\right)=\ell\left(AB\right)^2 \\ &\therefore A\left(\square ABCD\right)=\left(1\right)^2 \\ &\therefore A\left(\square ABCD\right)=1\end{aligned}
\therefore \square ABCD चं क्षेत्रफळ 1 चौरस मीटर आहे.
वर नमूद केल्याप्रमाणे \square ABCD प्रमाणे खोक्याला 6 पृष्ठभाग आहेत.
\therefore खोक्याचं पृष्ठफळ,
\begin{aligned} \\ &=6\times A\left(\square ABCD\right) \\ &=6\times 1 \\ &=6\end{aligned}
\mathbf{\therefore } खोक्याचं पृष्ठफळ 6 चौरस मीटर आहे.
घनफळ म्हणजे काय?
पृष्ठफळ व घनफळ यांची ओळख करून घेताना आपण आधी घनफळ म्हणजे काय ते पाहू,
वस्तूची एखादा पदार्थ सामावून घेण्याची जी क्षमता असते, ती घनफळात व्यक्त केली जाते.
उदाहरणार्थ,
(1) एखाद्या खोक्याची वस्तू सामावून घेण्याची क्षमता.
(2) घागरीची पाणी सामावून घेण्याची क्षमता.
(3) कॅनची दूध सामावून घेण्याची क्षमता.
(4) वाहनाच्या इंधन टाकीची इंधन सामावून घेण्याची क्षमता.
आपण एखादी घागर खरेदी करताना दुकानदाराला विचारतो की ही घागर किती लिटरची आहे; म्हणजे आपण त्या घागरीची साठवण क्षमता किती आहे ते विचारतो. ही साठवण क्षमता म्हणजेच त्या घागरीचं घनफळ असतं.
उदा: प्रत्येक बाजूची लांबी 10 मीटर असलेल्या टाकीचं घनफळ काढा (म्हणजेच टाकीची साठवण क्षमता काढा).
दिलेल्या टाकीची प्रत्येक बाजू ही समान लांबीची आहे आणि अशा प्रकारच्या त्रिमितीय आकाराला “घन” म्हणतात.
घनाचे घनफळ =l (लांबी) \times b (रुंदी) \times h (उंची)
पण घनाची प्रत्येक बाजू समान लांबीची असल्याने,
घनाचे घनफळ =(बाजूची लांबी)^3
\therefore टाकीचं घनफळ =\left(10\right)^3=1000 मीटर ^3
थोडक्यात, एखाद्या बादलीच्या साठवण क्षमतेला त्या बादलीचं घनफळ (Volume) म्हणतात आणि त्या बादलीच्या बाहेरच्या पृष्ठभागाच्या क्षेत्रफळाला त्या बादलीचं पृष्ठफळ (Surface Area) म्हणतात.
पृष्ठफळ व घनफळ ह्या संकल्पना समजावून घेण्यासाठी आपण घनफळाची काही उदाहरणं सोडवूया,
उदा 1:
प्रत्येक बाजूची लांबी 1 सेमी असलेले 6 घन आकृतीत दाखवल्याप्रमाणे एकमेकांना जोडून एक इष्टिकाचिती तयार करा आणि त्या इष्टिकाचितीचं घनफळ काढा.
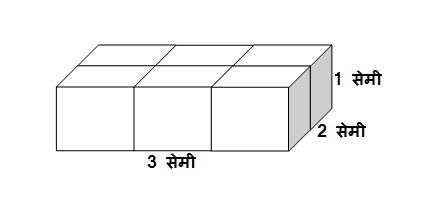
उत्तर:
6 घन मिळून तयार झालेल्या इष्टिकाचितीची लांबी 3 सेमी, रुंदी 2 सेमी आणि उंची 1 सेमी आहे.
इष्टिकाचितीचं घनफळ =(लांबी)\times (रुंदी)\times (उंची)
\therefore इष्टिकाचितीचं घनफळ =3\times 2\times 1=6 घन सेमी.
उदा 2:
प्रत्येक बाजूची लांबी 1 सेमी असलेले 12 घन आकृतीत दाखवल्याप्रमाणे एकमेकांना जोडून एक इष्टिकाचिती तयार करा आणि त्या इष्टिकाचितीचं घनफळ काढा.
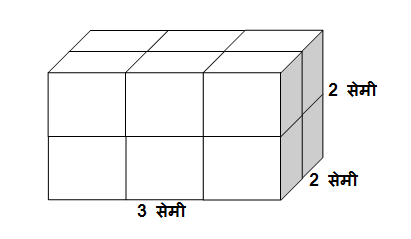
उत्तर:
12 घन मिळून तयार झालेल्या इष्टिकाचितीची लांबी 3 सेमी, रुंदी 2 सेमी आणि उंची 2 सेमी आहे.
इष्टिकाचितीचं घनफळ =(लांबी)\times (रुंदी)\times (उंची)
\therefore इष्टिकाचितीचं घनफळ =3\times 2\times 2=12 घन सेमी.
उदा 3:
प्रत्येक बाजूची लांबी 1 सेमी असलेले 12 घन आकृतीत दाखवल्याप्रमाणे एकमेकांना जोडून एक इष्टिकाचिती तयार करा आणि त्या इष्टिकाचितीचं घनफळ काढा.
उत्तर:
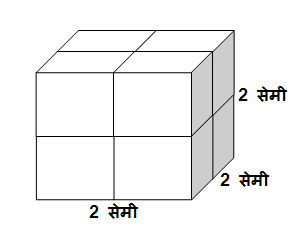
शेजारील आकृतीत 1 घन सेमी घनफळ असलेले 8 घन एकमेकांना चिकटून ठेवले आहेत. त्यामुळे मिळणारी घनाकृती ही बाजू 2 सेमी असलेला घन आहे.
ह्या घनाचे घनफळ =(लांबी)\times (रुंदी)\times (उंची)
\therefore घनफळ 2\times 2\times 2=2^3=8 घन सेमी.
द्रवाचे घनफळ
पृष्ठफळ व घनफळ ह्या संकल्पना समजावून घेण्यासाठी आपण द्रवाचे घनफळ कसे काढतात ते बघू,
द्रव पदार्थ ज्या भांड्यात, पिंपात किंवा टाकीत साठवला जातो, त्या भांड्याच्या, पिंपाच्या किंवा टाकीच्या घनफळाला त्या द्रवाचं घनफळ म्हणतात.
| महत्वाचं: द्रवाचे आकारमान हेच द्रवाचे घनफळ असते. |
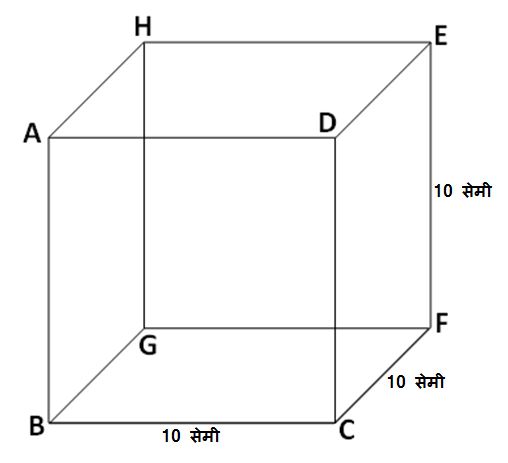
उदाहरण: वरील आकृतीमध्ये दर्शविलेल्या पाण्याच्या टाकीची प्रत्येक बाजू 10 सेमी लांबीची आहे. म्हणून ह्या टाकीचं घनफळ 10\times 10\times 10=1000 घन सेमी आहे.
म्हणजेच ही टाकी पाण्याने पूर्ण भरल्यास पाण्याचे आकारमान 1000 घन सेमी असेल. ह्या आकारमानालाच 1 लिटर असं म्हणतात.
1000 घन सेमी = 1 लिटर = 1000 मिली लिटर.
ह्याचा अर्थ प्रत्येक बाजू 1 सेमी लांबीची असलेल्या घनाकृती टाकीत मावणाऱ्या पाण्याचे आकारमान 1 मिली लिटर (मिली) असते.
उदाहरणं
पृष्ठफळ व घनफळ ह्या संकल्पना समजावून घेण्यासाठी आपण द्रवाच्या घनफळाची काही उदाहरणं सोडवूया,
उदा 1:
इष्टिकाचिती आकाराच्या, मासे ठेवण्याच्या काचेच्या पेटीची लांबी 1 मीटर, रुंदी 40 सेमी व उंची 50 सेमी आहे तर त्या पेटीत किती लीटर पाणी मावेल?
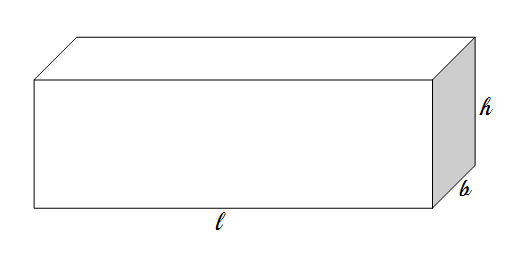
उत्तर:
लांबी (l) 1 मीटर = 100 सेमी
रुंदी (b) = 40 सेमी
उंची (h) = 50 सेमी
इष्टिकाचितीचं घनफळ V=(लांबी)\times (रुंदी)\times (उंची)
\therefore घनफळ =100\times 40\times 50
\therefore घनफळ =200000 घन सेमी
आता हे घनफळ लिटरमध्ये काढायला आपल्याला 1000 ने भागावं लागेल,
घनफळ =\frac{200000}{1000}=200 लिटर.
\mathbf{\therefore } मासे ठेवायच्या काचेच्या पेटीत 200 लिटर पाणी मावेल.
उदा 2:
एका इष्टिकाचिती आकाराच्या गोदामाची लांबी 6 मी, रुंदी 4 मी आणि उंची 4 मी आहे. या गोदामात 40 सेमी बाजू असलेली घनाकृती खोकी जास्तीत जास्त किती मावतील?
उत्तर:
लांबी (l) = 6 मीटर = 600 सेमी
रुंदी (b) = 4 मी = 400 सेमी
उंची (h) = 4 मी = 400 सेमी
इष्टिकाचितीचं घनफळ =(लांबी)\times (रुंदी)\times (उंची)
\therefore घनफळ =600\times 400\times 400
\therefore घनफळ =9,60,00,000 घन सेमी
\therefore गोदामाचं घनफळ 9,60,00,000 घन सेमी आहे.
आता आपण एका खोक्याचं घनफळ काढून घेऊ,
खोक्याचं घनफळ V=(लांबी)\times (रुंदी)\times (उंची)
\therefore घनफळ =40\times 40\times 40
\therefore घनफळ =64,000 घन सेमी
\therefore एका खोक्याचं घनफळ 64,000 घन सेमी आहे.
आता ह्या गोदामात 64,000 घन सेमी घनफळाची किती खोकी मावतील, हे काढण्यासाठी आपल्याला गोदामाच्या घनफळाला एक खाक्याच्या घनफळाने भागावं लागणार आहे.
=\frac{9,60,00,000}{64,000}=1500
\mathbf{\therefore } या गोदामात 40 सेमी बाजू असलेली घनाकृती 1500 खोकी मावतील.
उदा 3:
बर्फी तयार करण्यासाठी खवा व साखर यांचे वितळलेले 5 लीटर मिश्रण इष्टिकाचिती आकाराच्या ट्रेमध्ये ओतल्यास तो ट्रे काठोकाठ भरतो. ट्रेची रुंदी 40 सेमी व उंची 2.5 सेमी असल्यास त्याची लांबी काढा.
उत्तर:
खवा आणि साखर ह्यांचं मिश्रण 5 लिटर आहे आणि ते मिश्रण दिलेल्या ट्रेमध्ये ओतल्यावर ट्रे काठोकाठ भरतो, म्हणजे ट्रेची साठवण क्षमताही 5 लिटर आहे.
आपण आधी पाहिलं आहे की,
1 मिली लिटर = 1 घन सेंटीमीटर
\therefore 1 लिटर = 1000 घन सेंटीमीटर
\therefore 5 लिटर = 5000 घन सेंटीमीटर
इष्टिकाचितीचं घनफळ V=(लांबी)\times (रुंदी)\times (उंची)
\begin{aligned} \\ &\therefore 5000=\ell\times 40\times 2.5 \\ &\therefore 5000=\ell\times 100 \\ &\therefore \frac{5000}{100}=\ell\times \frac{100}{100} \\ &\therefore 50=\ell\times 1 \\ &\therefore \ell=50\end{aligned}
\mathbf{\therefore } ट्रेची लांबी 50 सेमी आहे.
उदा 4:
एका खोक्याची लांबी 20 सेमी, रुंदी 10.5 सेमी व उंची 8 सेमी असल्यास त्याचे घनफळ काढा.
उत्तर:
लांबी (l) = 20 सेमी
रुंदी (b) = 10.5 सेमी
उंची (h) = 8 सेमी
खोक्याचं घनफळ V=(लांबी)\times (रुंदी)\times (उंची)
\begin{aligned} \\ & \therefore V=20\times 10.5\times 8 \\ & \therefore V=1680\end{aligned}
\mathbf{\therefore } खोक्याचं घनफळ 1680 घन सेमी आहे.
उदा 5:
एका इष्टिकाचिती आकाराच्या साबणाच्या वडीचे घनफळ 150 घसेमी आहे. तिची लांबी 10 सेमी व रुंदी 5 सेमी असेल तर तिची जाडी किती असेल?
उत्तर:
घनफळ V = 150 घसेमी
लांबी (l) = 10 सेमी
रुंदी (b) = 5 सेमी
जाडी / उंची (h) = ? सेमी
खोक्याचं घनफळ V=(लांबी)\times (रुंदी)\times (उंची)
\begin{aligned} \\ & \therefore 150=10\times 5\times h \\ & \therefore 150=50\times h \\ & \therefore \frac{150}{50}=\frac{50}{50}\times h \\ & \therefore h=3\end{aligned}
\mathbf{\therefore } वडीची जाडी 3 सेमी आहे.
उदा 6:
6 मीटर लांब, 2.5 मी उंच व 0.5 मी रुंद अशी भिंत बांधायची आहे यासाठी 25 सेमी लांबी, 15 सेमी रुंदी व 10 सेमी उंचीच्या किती विटा लागतील?
उत्तर:
भिंतीची लांबी (l) = 6 मीटर = 600 सेमी
भिंतीची रुंदी (b) = 2.5 मी = 250 सेमी
भिंतीची उंची (h) = 0.5 मी = 50 सेमी
भिंतीचं घनफळ V_1=(लांबी)\times (रुंदी)\times (उंची)
\therefore V_1=600\times 250\times 50
\therefore V_1=75,00,000 घन सेमी
\therefore भिंतीचं घनफळ 75,00,000 घन सेमी आहे.
विटेची लांबी (l) = 25 सेमी
विटेची रुंदी (b) = 15 सेमी
विटेची उंची (h) = 10 सेमी
आता आपण एका विटेचं घनफळ काढून घेऊ,
विटेचं घनफळ V_2=(लांबी)\times (रुंदी)\times (उंची)
\therefore V_2=25\times 15\times 10
\therefore V_2=3,750 घन सेमी
\therefore एका विटेचं घनफळ 3,750 घन सेमी आहे.
आता 75,00,000 घन सेमी घनफळाची भिंत बांधायला आपल्याला किती विटा लागणार आहेत ते काढण्यासाठी आपल्याला भिंतीच्या घनफळाला एका विटेच्या घनफळाने भागावं लागणार आहे.
\begin{aligned} \\ &\therefore V=\frac{V_1}{V_2} \\ &\therefore V=\frac{75,00,000}{3750} \\ &\therefore V=2000\end{aligned}
\mathbf{\therefore } 75,00,000 घन सेमी घनफळाची भिंत बांधायला 2000 विटा लागतील.
उदा 7:
पावसाचे पाणी साठवण्यासाठी एका वसाहतीत 10 मी लांब, 6 मी रुंद व 3 मी खोल अशा मापांची टाकी बांधून घेतली आहे. तर त्या टाकीची धारकता किती आहे? टाकीत किती लीटर पाणी मावेल?
उत्तर:
टाकीची लांबी (l) = 10 मी
टाकीची रुंदी (b) = 6 मी
टाकीची उंची (h) = 3 मी
टाकीचं घनफळ V=(लांबी)\times (रुंदी)\times (उंची)
\begin{aligned} \\ &\therefore V=10\times 6\times 3 \\ &\therefore V=180\end{aligned}
\mathbf{\therefore } टाकीचं घनफळ 180 घन मीटर आहे.
आपण आधी पाहिलं आहे की,
1 मिली लिटर = 1 घन सेंटीमीटर
\therefore 1000 मिली लिटर = 1000 घन सेंटीमीटर
\therefore 1 लिटर = 1000 घन सेंटीमीटर
1 मीटर = 100 सेंटीमीटर
\therefore 1 घन मीटर =100\times 100\times 100
\therefore 1 घन मीटर =10,00,000 घन सेंटीमीटर
\therefore 180 घन मीटर =180\times 1000000=18,00,00,000 घन सेंटीमीटर
\therefore 180 घन मीटर =18,00,00,000/1000=1,80,000 लिटर
\mathbf{\therefore } टाकीत 1,80,000 लिटर पाणी मावेल.
वृत्तचितीचे पृष्ठफळ
पृष्ठफळ व घनफळ ह्या संकल्पना समजावून घेण्यासाठी वृत्तचितीचे पृष्ठफळ कसे काढतात, ते पाहू,
खालील चित्रात दाखवल्याप्रमाणे आपल्या घरात जे गोल आकाराचे उभट डबे असतात, त्या आकाराला वृत्तचिती असं म्हणतात.

वृत्तचिती आकाराच्या वस्तूंच्या पृष्ठफळला वक्रपृष्ठफळ म्हणतात. वक्रपृष्ठफळ काढण्यासाठी त्या वृत्तचितीच्या उंची इतकी रुंदी असलेला एक आयताकृती कागद त्या वृत्तचितीला असा गुंडाळतात की, आकृतीत दाखवल्याप्रमाणे कागदाची सुरुवात आणि शेवट एकाच रेषाखंडावर होते (आकृतीत रेख AB).
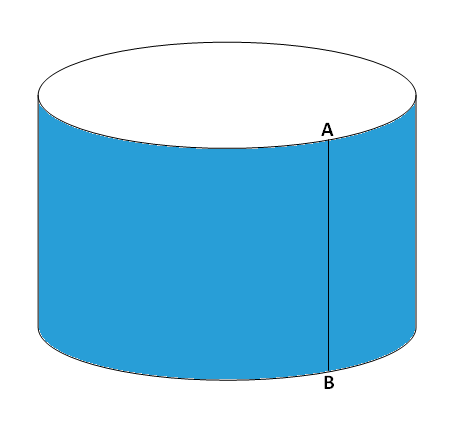
इथे लक्षात घ्या की गुंडाळलेला कागद हा आयताकृती आहे. ह्या आयताकृती कागदाचं क्षेत्रफळ = लांबी \times रुंदी
\therefore वृत्तचितीचे वक्रपृष्ठफळ = आयताचे क्षेत्रफळ = लांबी \times रुंदी.
(1) वृत्तचितीला गुंडाळलेल्या कागदाची लांबी = वृत्तचितीच्या तळाचा परीघ
(2) वृत्तचितीला गुंडाळलेल्या कागदाची रुंदी = वृत्तचितीची उंची
| \mathbf{\therefore } वृत्तचितीचे वक्रपृष्ठफळ = (वृत्तचितीच्या तळाचा परीघ) \mathbf{\times} (वृत्तचितीची उंची) \mathbf{\therefore } वृत्तचितीचे वक्रपृष्ठफळ = \mathbf{2\pi r\times h=2 \pi rh} |
बंदिस्त वृत्तचितीचं संपूर्ण पृष्ठफळ:
बंदिस्त वृत्तचितीचं संपूर्ण पृष्ठफळ काढण्यासाठी आपल्याला त्या वृत्तचितीच्या वरच्या आणि खालच्या वर्तुळाकृती पृष्ठांचं क्षेत्रफळही विचारात घ्यावं लागेल.
\therefore बंदिस्त वृत्तचितीचं एकूण पृष्ठफळ = (वृत्तचितीचं व्रकपृष्ठफळ) + (वरच्या वर्तुळाकृती पृष्ठाचं क्षेत्रफळ) + (तळाच्या वर्तुळाकृती पृष्ठाचं क्षेत्रफळ)
\therefore बंदिस्त वृत्तचितीचं एकूण पृष्ठफळ = (वृत्तचितीचं व्रकपृष्ठफळ) + 2\times (वर्तुळाचं क्षेत्रफळ)
\therefore बंदिस्त वृत्तचितीचं एकूण पृष्ठफळ =\therefore 2\pi rh + 2\pi r^2
\therefore बंदिस्त वृत्तचितीचं एकूण पृष्ठफळ =\therefore 2\pi r\left(h+r\right)
| \mathbf{\therefore } बंदिस्त वृत्तचितीचं एकूण पृष्ठफळ \mathbf{=\therefore 2\pi r\left(h+r\right)} |
उदाहरणं
पृष्ठफळ व घनफळ ह्या संकल्पना समजावून घेण्यासाठी वृत्तचितीच्या पृष्ठफळाची काही उदाहरणं सोडवू,
उदा 1:
एका वृत्तचिती आकाराच्या पाण्याच्या टाकीचा व्यास 1 मीटर आणि उंची 2 मीटर आहे. टाकीला झाकण लावले आहे. झाकणासह टाकीला आतून व बाहेरून रंग लावायचा आहे. रंगाचा खर्च 80 रुपये प्रति चौमी आहे. तर टाकी रंगवण्यासाठी किती खर्च येईल?
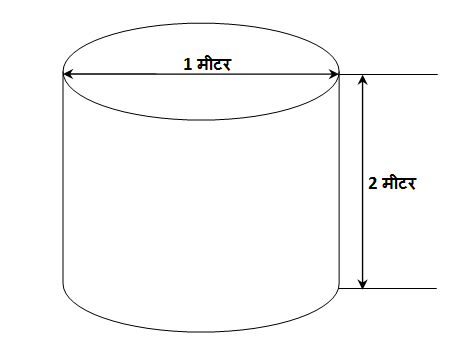
उत्तर:
(1) बंदिस्त वृत्तचितीचा त्रिज्या (r) = \frac{1}{2}\times (व्यास) = \frac{1}{2}\times 1 = 0.5 मीटर
(2) बंदिस्त वृत्तचितीची उंची (h) = 2 मीटर
(3) \pi =3.14
(4) रंग लावायचा प्रति चौरा मीटर दर = 80 रुपये
पायरी 1:
बंदिस्त वृत्तचितीचं एकूण पृष्ठफळ A=2\pi r\left(h+r\right)
\begin{aligned} \\ &\therefore A=2\times \left(3.14\right)\times \left(0.5\right)\times \left(2+0.5\right) \\ &\therefore A=\left(3.14\right)\times \left(2.5\right) \\ &\therefore A=7.85\end{aligned}
\therefore बंदिस्त टाकीचं पृष्ठफळ 7.85 चौरस मीटर आहे.
पायरी 2:
आपल्याला टाकीच्या आतून आणि बाहेरून असा दोन्ही बाजूंनी रंग लावायचा आहे.
त्यामुळे रंग लावायच्या एकूण पृष्ठाचं पृष्ठफळ A=2\times (बंदिस्त टाकीचं पृष्ठफळ)
\begin{aligned} \\ &\therefore A=2\times \left(7.85\right) \\ &\therefore A=15.7\end{aligned}
\therefore बंदिस्त टाकीच्या रंग लावायच्या पृष्ठाचं एकूण पृष्ठफळ 15.7 चौरस मीटर आहे.
पायरी 3:
बंदिस्त टाकीला आतून आणि बाहेरून रंग लावायचा खर्च = (बंदिस्त टाकीच्या रंग लावायच्या पृष्ठाचं एकूण पृष्ठफळ) \times (प्रति चौरस मीटर दर)
बंदिस्त टाकीला आतून आणि बाहेरून रंग लावायचा खर्च = \mathbf{15.7\times 80=1256} रुपये.
उदा 2:
जस्ताच्या एका आयताकार पत्र्याची लांबी 3.3 मीटर व रुंदी 3 मीटर आहे. या पत्र्यापासून 3.5 सेमी त्रिज्येच्या आणि 30 सेमी लांबीच्या जास्तीत जास्त किती नळ्या तयार करता येतील?
उत्तर:
(1) पत्र्याची लांबी = 3.3 मीटर = 330 सेमी
(2) पत्र्याची रुंदी = 3 मीटर = 300 सेमी
(3) तयार करायच्या नळ्यांची त्रिज्या = 3.5 सेमी
(4) तयार करायच्या नळ्यांची लांबी = 30 सेमी
पायरी 1:
जस्ताच्या आयताकार पत्र्याचं क्षेत्रफळ/पृष्ठफळ A1= (लांबी) \times (रुंदी)
\begin{aligned} \\ &\therefore A_1=\left(330\right)\times \left(300\right) \\ &\therefore A_1=99,000\end{aligned}
जस्ताच्या आयताकार पत्र्याचं क्षेत्रफळ/पृष्ठफळ 99,000 चौरस सेमी आहे.
पायरी 2:
दिलेल्या जस्ताच्या पत्र्यापासून तयार करायच्या नळ्यांचं वक्रपृष्ठफळ A_2=2\pi rh
\begin{aligned} \\ &\therefore A_2=2\times \frac{22}{7}\times \frac{35}{10}\times 30 \\ &\therefore A_2=2\times \frac{22}{\cancel{7}}\times \frac{\cancel{35}^5}{\cancel{10}}\times \cancel{30}^3 \\ &\therefore A_2=2\times 22\times 5\times 3 \\ &\therefore A_2=660\end{aligned}
दिलेल्या जस्ताच्या पत्र्यापासून तयार करायच्या नळ्यांचं वक्रपृष्ठफळ 660 चौरस सेमी आहे.
पायरी 3:
दिलेल्या 99,000 चौरस सेमी पृष्ठफळाच्या (क्षेत्रफळाच्या) जस्ताच्या पत्र्यापासून 660 चौरस सेमी वक्रपृष्ठफळाच्या किती नळ्या तयार करता येतील हे काढण्यासाठी आपल्याला जस्ताच्या पत्र्याच्या पृष्ठफळाला नळ्यांच्या वक्रपृष्ठफळाने भागावं लागेल.
\mathbf{\therefore } जस्ताच्या पत्र्यापासून तयार होणाऱ्या नळ्यांची संख्या \mathbf{=\frac{A_1}{A_2}=\frac{99,000}{660}=150}
उदा 3:
खालील प्रत्येक उदाहरणात वृत्तचितीच्या पायाची त्रिज्या r व उंची h दिली आहे; त्यावरून प्रत्येक वृत्तचितीचे वक्रपृष्ठफळ आणि एकूण पृष्ठफळ काढा.
उत्तर:
| अनुक्रमांक | वृत्तचितीच्या पायाची त्रिज्या (r) | वृत्तचितीची उंची (h) | वृत्तचितीचे वक्रपृष्ठफळ A=2 \pi rh | वृत्तचितीचे एकूण पृष्ठफळ A=2\pi r\left(h+r\right) |
|---|---|---|---|---|
| 1. | 7 सेमी | 10 सेमी | \begin{aligned} \\ &\therefore A=2 \times \frac{22}{7}\times 7\times 10 \\ &\therefore A=2 \times 22\times 10 \\ &\therefore A=440\end{aligned} A=440 चौरस सेमी | \begin{aligned} \\ &\therefore A=2 \times \frac{22}{7}\times 7\times \left(10+7\right) \\ &\therefore A=2 \times 22\times 17 \\ &\therefore A=748\end{aligned} A=748 चौरस सेमी |
| 2. | 1.4 सेमी | 2.1 सेमी | \begin{aligned} \\ &\therefore A=2 \times \frac{22}{7}\times 1.4\times 2.1 \\ &\therefore A=2 \times 22\times 0.2\times 2.1 \\ &\therefore A=18.48\end{aligned} A=18.48 चौरस सेमी | \begin{aligned} \\ &\therefore A=2 \times \frac{22}{7}\times 1.4\times \left(1.4+2.1\right) \\ &\therefore A=2 \times \frac{22}{7}\times 1.4\times 3.5 \\ &\therefore A=2 \times 22\times 0.2\times 3.5 \\ &\therefore A=30.8\end{aligned} A=30.80 चौरस सेमी |
| 3. | 2.5 सेमी | 7 सेमी | \begin{aligned} \\ &\therefore A=2 \times \frac{22}{7}\times 2.5\times 7 \\ &\therefore A=2 \times 22\times 2.5 \\ &\therefore A=18.48\end{aligned} A=110 चौरस सेमी | \begin{aligned} \\ &\therefore A=2 \times \frac{22}{7}\times 2.5\times \left(2.5+7\right) \\ &\therefore A=2 \times \frac{22}{7}\times 2.5\times 9.5 \\ &\therefore A=\frac{1045}{7} \\ &\therefore A=149.29\end{aligned} A=149.29 चौरस सेमी |
| 4. | 70 सेमी | 1.4 सेमी | \begin{aligned} \\ &\therefore A=2 \times \frac{22}{7}\times 70\times 1.4 \\ &\therefore A=2 \times 22\times 10\times 1.4 \\ &\therefore A=616\end{aligned} A=616 चौरस सेमी | \begin{aligned} \\ &\therefore A=2 \times \frac{22}{7}\times 70\times \left(70+1.4\right) \\ &\therefore A=2 \times 22\times 10\times 71.4 \\ &\therefore A=31,416\end{aligned} A=31,416 चौरस सेमी |
| 5. | 4.2 सेमी | 14 सेमी | \begin{aligned} \\ &\therefore A=2 \times \frac{22}{7}\times 4.2\times 14 \\ &\therefore A=2 \times 22\times 0.6\times 14 \\ &\therefore A=369.6\end{aligned} A=369.60 चौरस सेमी | \begin{aligned} \\ &\therefore A=2 \times \frac{22}{7}\times 4.2\times \left(4.2+14\right) \\ &\therefore A=2 \times 22\times 0.6\times 18.2 \\ &\therefore A=480.48\end{aligned} A=480.48 चौरस सेमी |
उदा 4:
दोन्ही बाजू बंद असलेल्या, 50 सेमी व्यास व 45 सेमी उंचीच्या पिंपाचे एकूण पृष्ठफळ काढा.
उत्तर:
(1) पिंपाची त्रिज्या r = व्यास /2 = \frac{50}{2}=25 सेमी
(2) पिंपाची उंची h = 45 सेमी
पिंपाचं एकूण पृष्ठफळ A=2\pi r\left(h+r\right)
\begin{aligned} \\ &\therefore A=2\times \left(3.14\right)\times \left(25\right)\times \left(25+45\right) \\ &\therefore A=2\times \left(3.14\right)\times \left(25\right)\times \left(70\right) \\ &\therefore A=2\times \left(3.14\right)\times \left(25\right)\times \left(25+45\right) \\ &\therefore A=10,990\end{aligned}
पिंपाचं एकूण पृष्ठफळ 10,990 चौरस सेमी आहे.
उदा 5:
एका वृत्तचितीचे वक्रपृष्ठफळ 660 चौसेमी व उंची 21 सेमी आहे, तर तिची त्रिज्या व तळाचे क्षेत्रफळ काढा.
उत्तर:
(1) वृत्तचितीचं वक्रपृष्ठफळ = 660 चौसेमी
(2) वृत्तचितीची उंची h = 21 सेमी
पायरी 1:
वृत्तचितीचं वक्रपृष्ठफळ A=2 \pi rh
\begin{aligned} \\ &\therefore 660=2\times \frac{22}{7}\times r\times 21 \\ &\therefore 660=2\times 22\times r\times 3 \\ &\therefore 660=132\times r \\ &\therefore \frac{660}{132}=\frac{132}{132}\times r \\ &\therefore r=5\end{aligned}
वृत्तचितीची त्रिज्या 5 सेमी आहे.
पायरी 2:
वृत्तचितीच्या तळाचं क्षेत्रफळ A=\pi r^2
\begin{aligned} \\ &\therefore A=3.14\times 5^2 \\ &\therefore A=3.14\times 25 \\ &\therefore A=78.50\end{aligned}
वृत्तचितीच्या तळाचं क्षेत्रफळ 78.50 चौरस सेमी आहे.
उदा 6:
एका वृत्तचिती आकाराच्या पत्र्याच्या डब्याचा व्यास 28 सेमी आहे व त्याची उंची 20 सेमी आहे. तो एका बाजूने उघडा आहे तर त्यासाठी लागलेल्या पत्र्याचे क्षेत्रफळ काढा. त्या डब्यास 2 सेमी उंचीचे झाकण तयार करण्यासाठी अंदाजे किती चौसेमी पत्रा लागेल ते काढा.
उत्तर:
(1) पत्र्याच्या डब्याची त्रिज्या r = व्यास/2 = \frac{28}{2}=14 सेमी
(2) पत्र्याची उंची h = 20 सेमी
पायरी 1:
वृत्तचितीचं वक्रपृष्ठफळ A=2 \pi rh
\begin{aligned} \\ &\therefore 660=2\times \left(\frac{22}{7}\right)\times \left(r\right)\times \left(21\right) \\ &\therefore 660=2\times \left(22\right)\times \left(r\right)\times \left(3\right) \\ &\therefore 660=132\times r \\ &\therefore \frac{660}{132}=\frac{132}{132}\times r \\ &\therefore r=5\end{aligned}
वृत्तचितीची त्रिज्या 5 सेमी आहे.
पायरी 2:
वृत्तचितीच्या तळाचं क्षेत्रफळ A=\pi r^2
\begin{aligned} \\ &\therefore A=3.14\times 5^2 \\ &\therefore A=3.14\times 25 \\ &\therefore A=78.50\end{aligned}
वृत्तचितीच्या तळाचं क्षेत्रफळ 78.50 चौरस सेमी आहे.
वृत्तचितिचं घनफळ
पृष्ठफळ व घनफळ ह्या संकल्पना समजावून घेण्यासाठी वृत्तचितीचे घनफळ कसे काढतात, ते पाहू,
वृत्तचिती आकाराच्या पात्राची साठवण क्षमता काढण्यासाठी त्या पात्राचं घनफळ काढावं लागतं.
कोणत्याही चितीचं घनफळ = (त्या चितीच्या तळाच्या पृष्ठभागाचं क्षेत्रफळ) \times (त्या चितीची उंची)
वृत्तचितीचा तळ हा वर्तुळाकार असल्याने वृत्तचितीचं क्षेत्रफळ =\pi r^2\times h
| \mathbf{\therefore }वृत्तचितीचं घनफळ \mathbf{V=\pi r^2\times h} |
उदाहरणं
पृष्ठफळ व घनफळ ह्या संकल्पना समजावून घेण्यासाठी वृत्तचितीच्या घनफळाची काही उदाहरणं सोडवू,
उदा 1:
एका वृत्तचितीच्या तळाची त्रिज्या 5 सेमी असून तिची उंची 10 सेमी आहे. तर त्या वृत्तचितीचे घनफळ काढा.
उत्तर:
(1) वृत्तचितीच्या तळाची त्रिज्या r = 5 सेमी
(2) वृत्तचितीची उंची h = 10 सेमी
वृत्तचितीचं घनफळ A=\pi r^2\times h
\begin{aligned} \\ &\therefore A=3.14\times 5^2\times 10 \\ &\therefore A=3.14\times 25\times 10 \\ &\therefore A=785\end{aligned}
वृत्तचितीचं घनफळ 785 घन सेमी आहे.
उदा 2:
एका वृत्तचिती आकाराच्या पिंपाची उंची 56 सेमी आहे. त्या पिंपाची धारकता 70.4 लीटर आहे. तर त्या पिंपाची त्रिज्या काढा.
उत्तर:
(1) पिंपाची धारकता V = 70.4 लीटर = 70,400 घन सेमी
(2) पिंपाची उंची h = 56 सेमी
पिंपाचं घनफळ A=\pi r^2\times h
\begin{aligned} \\ &\therefore 70,400=\frac{22}{7}\times r^2\times 56 \\ &\therefore 70,400=22\times r^2\times 8 \\ &\therefore 70,400=176\times r^2 \\ &\therefore \frac{70,400}{176}=\frac{176}{176}\times r^2 \\ &\therefore r^2=400 \\ &\therefore r=\sqrt{400} \\ &\therefore r=20\end{aligned}
पिंपाची त्रिज्या 20 सेमी आहे.
उदा 3:
तांब्याच्या भरीव वृत्तचितीच्या तळाची त्रिज्या 4.2 सेमी असून तिची उंची 16 सेमी आहे. ती वितळवून 1.4 सेमी व्यास व 0.2 सेमी जाडी असलेल्या किती चकत्या तयार करता येतील?
उत्तर:
(1) वृत्तचितीच्या तळाची त्रिज्या r1 = 4.2 सेमी
(2) वृत्तचितीची उंची h1 = 16 सेमी
(3) तयार करायच्या चकत्यांची त्रिज्या r2 = व्यास /2 = \frac{1.4}{2}=0.7 सेमी
(4) तयार करायच्या चकत्यांची जाडी h2 = 0.2 सेमी
पायरी 1:
वृत्तचितीचं घनफळ A_1=\pi r_1^2\times h_1
\begin{aligned} \\ &\therefore A_1=\pi \times 4.2^2\times 16 \\ &\therefore A_1=\pi \times 4.2\times 4.2\times 16\end{aligned}
पायरी 2:
एका चकतीचं A_2=\pi r_2^2\times<sub> </sub>h_2
\begin{aligned} \\ &\therefore A_2=\pi \times 0.7^2\times 0.2 \\ &\therefore A_2=\pi \times 0.7\times 0.7\times 0.2\end{aligned}
पायरी 3:
वितळवलेल्या तांब्याच्या भरीव वृत्तचितीपासून तयार होणाऱ्या चकत्यांची संख्या = वृत्तचितीचं घनफळ / एका चकतीचं घनफळ
\begin{aligned} \\ &=\frac{A_1}{A_2} \\ &=\frac{\pi\times 4.2\times 4.2\times 16}{\pi\times 0.7\times 0.7\times 0.2} \\ &=\frac{4.2\times 4.2\times 16}{\pi \times 0.7\times 0.7\times 0.2} \\ &=6\times 6\times 80 \\ &=2880\end{aligned}
वितळवलेल्या तांब्याच्या भरीव वृत्तचितीपासून 2880 चकत्या तयार करता येतील.
उदा 4:
खाली वृत्तचितीच्या तळाची त्रिज्या (r) व उंची (h) दिली आहे त्यावरून वृत्तचितीचे घनफळ काढा.
उत्तर:
| अनुक्रमांक | वृत्तचितीच्या तळाची त्रिज्या (r) | वृत्तचितीची उंची (h) | वृत्तचितीचे घनफळ V=\pi r^2h |
|---|---|---|---|
| 1. | 10.5 सेमी | 8 सेमी | \begin{aligned} \\ &\therefore V=\frac{22}{7}\times 10.5^2\times 8 \\ &\therefore V=\frac{22}{7}\times 10.5\times 10.5\times 8 \\ &\therefore V=\frac{22}{7}\times 1.5\times 10.5\times 8 \\ &\therefore V=2772\end{aligned} V=2772 घन सेमी |
| 2. | 2.5 मी | 7 मी | \begin{aligned} \\ &\therefore V=\frac{22}{7}\times 2.5^2\times 7 \\ &\therefore V=22\times 2.5\times 2.5 \\ &\therefore V=137.5\end{aligned} V=137.5 घन मी |
| 3. | 4.2 सेमी | 5 सेमी | \begin{aligned} \\ &\therefore V=\frac{22}{7}\times 4.2^2\times 5 \\ &\therefore V=\frac{22}{7}\times 4.2\times 4.2\times 5 \\ &\therefore V=22\times 0.6\times 4.2\times 5 \\ &\therefore V=277.20\end{aligned} V=277.20 घन सेमी |
| 4. | 5.6 सेमी | 5 सेमी | \begin{aligned} \\ &\therefore V=\frac{22}{7}\times 5.6^2\times 5 \\ &\therefore V=\frac{22}{7}\times 5.6\times 5.6\times 5 \\ &\therefore V=22\times 0.8\times 5.6\times 5 \\ &\therefore V=492.80\end{aligned} V=492.80 घन सेमी |
उदा 5:
लांबी 90 सेमी व व्यास 1.4 सेमी असेल अशी लोखंडी सळई तयार करण्यासाठी लागणाऱ्या लोखंडाचे घनफळ काढा.
उत्तर:
(1) लोखंडी सळईची त्रिज्या r = (व्यास/2) = r=\frac{1.4}{2}=0.7
(2) लोखंडी सळईची लांबी/उंची h = 90 सेमी
लोखंडी सळईचं घनफळ V=\pi r^2\times h
\begin{aligned} \\ &\therefore V=\frac{22}{7}\times 0.7^2\times 90 \\ &\therefore V=\frac{22}{7}\times 0.49\times 90 \\ &\therefore V=22\times 0.07\times 90 \\ &\therefore V=138.60\end{aligned}
लोखंडी सळईचं घनफळ 138.60 घन सेमी आहे.
उदा 6:
वृत्तचिती आकाराच्या एका हौदाचा आतील व्यास 1.6 मी असून त्याची खोली 0.7 मी आहे, तर त्या हौदात जास्तीत जास्त किती पाणी मावेल?
उत्तर:
(1) हौदाचा आतील त्रिज्या r = (व्यास/2) = r=\frac{1.6}{2}=0.8 मी
(2) हौदाची खोली/उंची h = 0.7 मी
हौदाचं घनफळ V=\pi r^2\times h
\begin{aligned} \\ &\therefore V=\frac{22}{7}\times 0.8^2\times 0.7 \\ &\therefore V=\frac{22}{7}\times 0.64\times 0.7 \\ &\therefore V=22\times 0.64\times 0.1 \\ &\therefore V=1.408\end{aligned}
हौदाचं घनफळ 1.408 घन मी आहे.
1000 घन सेमी = 1000 मिली = 1 लिटर
1 घन मीटर = 100\times 100\times 100=10,00,000 घन सेमी = 10,00,000 मिली = \frac{10,00,000}{1000}=1000 लिटर
\therefore 1.408 घन मी = 1.408\times 1000=1408 लिटर
हौदात जास्तीत जास्त 1408 लिटर पाणी मावेल.
उदा 7:
एका वृत्तचितीच्या पायाचा परीघ 132 सेमी असून त्याची उंची 25 सेमी आहे, तर त्या वृत्तचितीचे घनफळ किती?
उत्तर:
पायरी 1:
वृत्तचितीचा पाया किंवा तळ हा वर्तुळाकार असतो.
वृत्तचतीच्या पायाचा परीघ = वर्तुळाचा परीघ P=2\pi r
\begin{aligned} \\ &\therefore 132=2\times \frac{22}{7}\times r \\ &\therefore 132\times 7=2\times \frac{22}{7}\times 7\times r \\ &\therefore 924=2\times 22\times r \\ &\therefore 924=44\times r \\ &\therefore \frac{924}{44}=\frac{44}{44}\times r \\ &\therefore r=21\end{aligned}
वृत्तचितीच्या पायाची त्रिज्या 21 सेमी
पायरी 2:
वृत्तचितीचं घनफळ V=\pi r^2\times h
\begin{aligned} \\ &\therefore V=\frac{22}{7}\times 21^2\times 25 \\ &\therefore V=\frac{22}{7}\times 441\times 25 \\ &\therefore V=22\times 63\times 25 \\ &\therefore V=34,650\end{aligned}
वृत्तचितीचं घनफळ 34,650 घन सेमी आहे.
इयत्ता 8 वी गणित पाठ्यपुस्तक: इथे क्लिक करा
