इयत्ता 8 वी परिमेय व अपरिमेय संख्या म्हणजे काय? : परिमेय व अपरिमेय संख्या संख्या हा गणितातील एक महत्त्वाचा विषय आहे. परिमेय व अपरिमेय संख्या समजून घेण्यासाठी आधी त्यांचा मूलभूत अर्थ लक्षात घेतला पाहिजे. परिमेय व अपरिमेय संख्या या दोन प्रकारांमध्ये संख्यांचे वर्गीकरण केले जाते. परिमेय संख्या त्या असतात ज्या दोन पूर्णांकांचे गुणोत्तर म्हणून व्यक्त करता येतात, तर अपरिमेय संख्या त्या असतात ज्या अशा स्वरूपात व्यक्त करता येत नाहीत.

संख्यांचे मूलभूत प्रकार
1) नैसर्गिक संख्या (Natural Numbers): ह्या संख्या समूहात धन पूर्णांक संख्यांचा समावेश होतो आणि ह्या समूहाची सुरुवात 1 ह्या आकड्यापासून होते.
नैसर्गिक संख्या समूह: \mathbf{1, 2, 3, 4 . . .}
2) पूर्ण संख्या समूह (Whole Numbers): ह्या संख्या समूहात देखील नैसर्गिक संख्या समूहाप्रमाणे धन पूर्णांक संख्यांचा समावेश होतो, पण ह्या संख्या समूहाची सुरुवात शून्यापासून होते.
पूर्ण संख्या समूह: \mathbf{0, 1, 2, 3, 4, . . .}
3) पूर्णांक संख्या समूह (Integers): ह्या संख्या समूहात धन आणि ऋण अशा दोन्ही पूर्ण संख्यांचा समावेश होतो.
पूर्णांक संख्या: . . . \mathbf{-4, -3, -2, -1, 0, 1, 2, 3, 4, . . .}
मित्रांनो, तुम्हाला वरील तीन संख्या समूह आणि त्यातील फरक काय आहे, हे आता पक्क लक्षात आलेलं आहे आणि त्यामुळे तुम्हाला परिमेय आणि अपरिमेय संख्या म्हणजे काय हे समजायला आता खूप सोपं जाणार आहे. चला तर मग आपण ह्या दोन्ही संकल्पना आता समजून घेऊयात.
परिमेय संख्या म्हणजे काय?
ज्या संख्या \mathbf{\frac{x}{y}} (x भागिले y) ह्या रूपात दर्शवता येतात त्यांना परिमेय संख्या म्हणतात. परिमेय संख्येत एक गोष्ट पक्की लक्षात ठेवायची की ह्या मध्ये \mathbf{x} आणि \mathbf{y} ह्या “पूर्ण संख्या” असतात पण \mathbf{y} हा कधीही शून्य नसतो. (पूर्ण संख्या म्हणजे काय ते वर 2 नंबरच्या परिच्छेदात दिलेले आहे).
परिमेय संख्या म्हणजे काय, हे समजावून घेण्यासाठी आता आपण परिमेय संख्यांचे काही गुणधर्म आणि उदाहरणं बघू म्हणजे तुम्हाला ही संकल्पना पूर्णपणे समजेल.
a) 5 ही संख्या परिमेय संख्या आहे कारण ती \frac{5}{1} अशी दर्शवता येऊ शकते (कारण 1 ने कोणत्याही संख्येला भागलं तरी मूळ संख्येची किंमत तीच राहते).
b) 0.5 ही संख्या \frac{1}{2} किंवा \frac{50}{100} अशी दर्शवता येऊ शकत असल्याने 0.5 ही संख्या परिमेय संख्या आहे.
c) \sqrt{81} ही देखील परिमेय संख्या आहे कारण 81 चे वर्गमूळ 9 आहे आणि 9 ही संख्या \frac{9}{1} अशी दर्शवता येऊ शकते.
d) ज्या संख्यांचे दशांश “खंडित (किंवा मर्यादित)” असतात किंवा “आवर्ती” स्वरूपाचे असतात, अशा संख्यांचा समावेश देखील परिमेय संख्यांमध्ये होतो. आता हे समजून घेण्यासाठी आपण काही उदाहरणं पाहुयात,
i) \frac{6}{5}= 1.2 या उदाहरणात 5 ने 6 ला पूर्ण भाग जात असल्याने 1.2 हे ” खंडित (किंवा मर्यादित)” उत्तर मिळते. “खंडित” म्हणजे 1.2 नंतर 5 ने 6 ला पूर्ण भाग जातो, म्हणजेच भागाकार पूर्ण होतो आणि त्यामुळे भागाकाराची क्रिया पुढे चालू ठेवता येत नाही.
ii) \frac{7}{6} = 1.1666666 . . . या उदाहरणात भागाकार पूर्ण होत नाही. प्रत्येक वेळी बाकी 40 येते आणि त्यामुळे भागाकार 6 येतो आणि ही क्रिया अमर्यादित काळासाठी चालू राहते; ह्यालाच “आवर्ती” स्वरूपाचा दशांश म्हणतात.
आता परिमेय संख्या म्हणजे काय, हे तुम्हला समजलं आहे; मग अपरिमेय संख्या म्हणजे काय ते तुमच्या सहज लक्षात येईल.
अपरिमेय संख्या म्हणजे काय?
ज्या संख्या \mathbf{\mathbf{\frac{x}{y}}} ह्या स्वरूपत दर्शवता येत नहीत, त्यांना “अपरिमेय संख्या” असं म्हणतात. म्हणजे कुठल्या संख्या, ते आपण त्यांच्या खालील गुणधर्मांवरून समजून घेऊयात,
i) ज्या संख्यांचा भाजक किंवा छेद हा शून्य असतो त्या अपरिमेय संख्या असतात.
उदा: \frac{3}{0} कारण आपण जेंव्हा शून्याने एखाद्या संख्येला भागतो तेंव्हा त्याचे उत्तर हे अनंत (Infinity) असते.
ii) \sqrt{2}, \sqrt{3}, \sqrt{5} आणि \sqrt{8} ह्या संख्या देखील अपरिमेय आहेत कारण ह्या संख्यांच्या वर्गमूळांच्या किमतीही अमर्याद दशांश स्वरूपाच्या असतात, परंतु आवर्ती नसतात. त्यामुळे ह्या संख्या
\frac{x}{y} ह्या स्वरूपात दर्शवता येत नाहीत.
\sqrt{2} = 1.41421356237 . . .
\sqrt{3} = 1.73205080757 . . .
iii) गणितातील स्थिरांक \pi (पाय) ही देखील एक अपरिमेय संख्या आहे कारण \pi ची किंमत देखील अमर्याद दशांश स्वरूपाची, परंतु आवर्ती स्वरूपाची नसते.
\mathbf{\pi = 3.1415926535 . . .}
परिमेय व अपरिमेय संख्यांमधील फरक
| अनुक्रमांक | परिमेय संख्या | अपरिमेय संख्या |
| 1 | दोन संख्यांचे गुणोत्तर म्हणून दर्शविल्या जाऊ शकतील अशा संख्यांना परिमेय संख्या म्हणतात. | दोन संख्यांचे गुणोत्तर म्हणून दर्शविल्या जाऊ शकत नाहीत, अशा संख्यांना अपरिमेय संख्या म्हणतात. |
| 2 | परिमेय संख्याचे दशांश हे मर्यादित असतात किंवा आवर्ती स्वरूपाचे असतात. | अपरिमेय संख्याचे दशांश हे अमर्यादित असतात, परंतु आवर्ती स्वरूपाचे नसतात. |
| 3 | पूर्ण वर्ग असलेल्या 4, 9, 16, 25, ... ह्या संख्यांचा समावेश परिमेय संख्यांमध्ये होतो. | \sqrt{2}, \sqrt{3}, \sqrt{5} आणि \sqrt{7} ह्या संख्यांचा समावेश अपरिमेय संख्यांमध्ये होतो. |
| 4 | परिमेय संख्यामध्ये अंश आणि भाजक (किंवा छेद) दोन्हीही पूर्ण संख्या असतात आणि भाजक कधीही शून्य नसतो. | अपरिमेय संख्या ह्या अंशात्मक स्वरूपात दर्शवता येत नाहीत. |
| 5 | उदाहरणं: 1) \frac{6}{5} = 1.2 (मर्यादित दशांश) 2) \frac{7}{6} = 1.1666666. . . (आवर्ती दशांश) | उदाहरणं: 1) \sqrt{2} = 1.41421356237 . . . 2) \pi = 3.1415926535 . . . वरील दोन्ही उदाहरणांत अमर्याद दशांश आहे, पण दशांश आवर्ती नाही. |
🔢 परिमेय / अपरिमेय संख्या तपासा
संख्यारेषेवर परिमेय संख्या दर्शवणे
आता आपण परिमेय संख्या संख्यारेषेवर कशा दर्शवायच्या, ते पाहू .
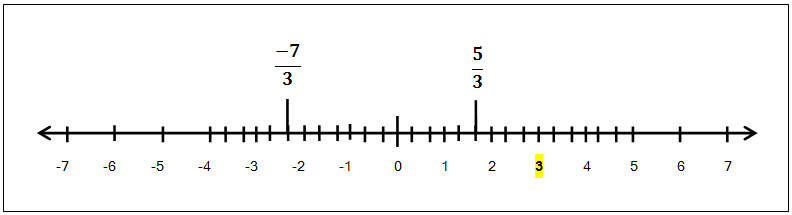
1) 3 ही संख्या आपण \frac{3}{1} अशी दर्शवू शकत असल्याने ती परिमेय संख्या आहे आणि ती आपण सहज संख्या रेषेवर दाखवू शकतो.
2) आता \frac{5}{3} ही धन संख्या संख्यारेषेवर कशी दाखवता येईल ते पाहू. \frac{5}{3} मध्ये भाजक (किंवा छेद) हा 3 आहे, म्हणून आपल्याला संख्यारेषेवरच्या प्रत्येक एककाचे 3 समान भाग आधी करून घ्यावे लागतील आणि त्यानंतर शून्याच्या उजवीकडील पाचवा बिंदू \frac{5}{3} ही संख्या दर्शवेल.
3) वरील नियम आपण ऋण संख्या \frac{-7}{3} साठीही लावू शकतो. आता संख्या ऋण असल्याने शून्याच्या डावीकडील सातवा बिंदू \frac{-7}{3} ही संख्या दर्शवेल.
खालील आकृती बघा म्हणजे तुमच्या लक्षात येईल.
मग आता वरील नियम वापरून \frac{5}{4} ही धन संख्या संख्यारेषेवर कशी दाखवता येईल?
सोपं आहे; आता भाजक 4 असल्याने आपल्याला आधी प्रत्येक एककाचे 4 भाग करावे लागतील आणि शून्याच्या उजवीकडील पाचवा बिंदू \frac{5}{4} ही संख्या दर्शवेल. तुम्ही हे उदाहरण स्वतः तुमच्या वहीत करून बघा.
अशा रीतीने आपण इतर धन आणि ऋण परिमेय संख्या सहज संख्यारेषेवर दर्शवू शकतो.
संख्यारेषेवर अपरिमेय संख्या दर्शवणे
परिमेय संख्यांप्रमाणेच अपरिमेय संख्या संख्यारेषेवर दाखवता येतात का?
तर ह्या प्रश्नाचं उत्तर आहे “हो, अपरिमेय संख्या देखील संख्यारेषेवर दर्शवता येतात”.
उदाहरण 1:
आपण \sqrt{2} ही संख्या संख्यारेषेवर कशी दर्शवता येते ते पाहू,
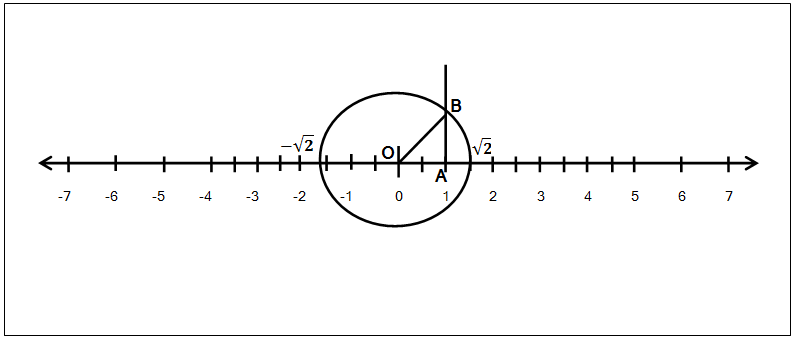
आता खालील कृती क्रमाने करू:
- संख्यारेषेवर शून्याच्या उजवीकडे बिंदू A हा 1 एकक दर्शवतो. म्हणजेच OA = 1 आहे.
- आता A बिंदूवर एक लंब काढा.
- ह्या लंबावर B हा एक बिंदू असा घ्या की OA = AB = 1.
- आता O आणि B हे बिंदू एका रेषेने जोडून OAB हा काटकोन त्रिकोण तयार करा.
- आता आपण पायथॅगोरसचा सिद्धांत वापरून त्रिकोण OAB च्या कर्णाची, म्हणजेच बाजू OB ची लांबी काढूयात,
\begin{aligned} \\ (OB)^{2}&=(OA)^{2} + (AB)^{2} \\ &=(1)^{2} + (1)^{2} \\ &=1 + 1 \\ &=\sqrt{2} \end{aligned}
आता सगळ्यात महत्वाचे: आता \sqrt{2} ही अपरिमेय संख्या संख्यारेषेवर दर्शविण्यासाठी आपण बिंदू O हे केंद्र आणि OB ही त्रिज्या घेऊन एक वर्तुळ काढूया. हे वर्तुळ संख्यारेषेला शून्याच्या उजवीकडे जेथे छेदते ती \sqrt{2} ही संख्या आहे आणि शून्याच्या डावीकडे जिथे छेदते ती \sqrt{-2} ही संख्या आहे.
उदाहरण 2:
वरील कृती वापरून आता आपण \mathbf{\sqrt{3}} ही संख्या संख्या रेषेवर दर्शवुयात,
आता लक्ष देऊन बघा की आपल्याला वरील \sqrt{2} आकृतीत, \sqrt{3} साठी काय महत्वाचा बदल करायचा आहे. हे एकदा तुम्हाला कळलं की त्या पुढील कोणतीही अपरिमेय संख्या तुम्ही संख्यारेषेवर सहज दर्शवू शकाल.
- महत्वाचे: वरील \sqrt{2} च्या आकृतीमध्ये आता A हा बिंदू आता आपल्याला \sqrt{2} चा जो बिंदू आहे तिथपर्यंत उजवीकडे सरकवायचा आहे. म्हणजे A हा बिंदू \sqrt{2} ही संख्या दर्शवेल. म्हणजेच OA ची लांबी आता \sqrt{2} झाली आहे.
- आता A बिंदूवर एक लंब काढा.
- ह्या लंबावर B हा एक बिंदू असा घ्या की AB = 1.
- आता O आणि B हे बिंदू एका रेषेने जोडून OAB हा काटकोन त्रिकोण तयार करा.
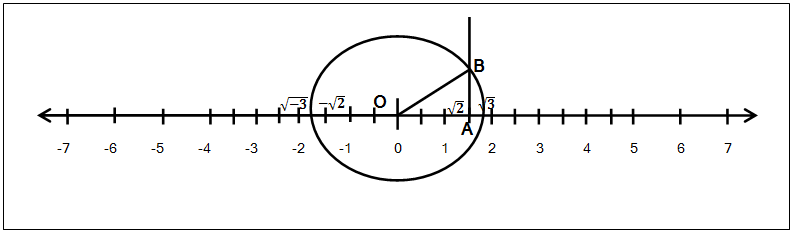
- आता आपण पायथॅगोरसचा सिद्धांत वापरून त्रिकोण OAB च्या कर्णाची, म्हणजेच बाजू OB ची लांबी काढूयात,
\begin{aligned} \\ (OB)^{2}&=(OA)^{2} + (AB)^{2} \\ &=(\sqrt{2})^{2} + (1)^{2} \\ &= 2 + 1 \\ &=\sqrt{3}\end{aligned}
- आता सगळ्यात महत्वाचे: आता \sqrt{3} ही अपरिमेय संख्या संख्यारेषेवर दर्शविण्यासाठी आपण बिंदू O हे केंद्र आणि OB ही त्रिज्या घेऊन एक वर्तुळ काढूया. हे वर्तुळ संख्यारेषेला शून्याच्या उजवीकडे जेथे छेदते ती \sqrt{3} ही संख्या आहे आणि शून्याच्या डावीकडे जिथे छेदते ती \sqrt{-3} ही संख्या आहे.
उदाहरण 3:
आता \sqrt{4} ही संख्या, संख्यारेषेवर कशी दर्शवता येईल? सोपं आहे! पहिली गोष्ट म्हणजे \mathbf{\sqrt{4}} ही अपरिमेय संख्या नसून ही एक परिमेय संख्या आहे; कारण 4 चे वर्गमूळ 2 असते आणि 2 ही संख्या आपण \mathbf{\frac{2}{1}} अशी दर्शवू शकतो.
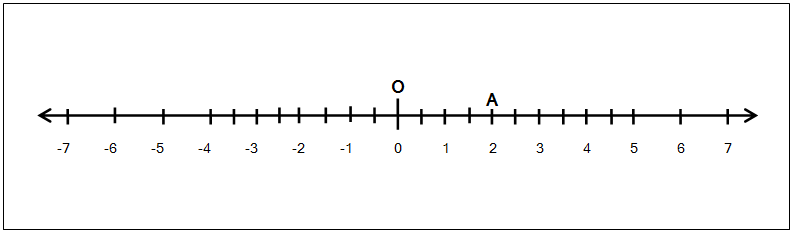
वरील आकृतीत A हा बिंदू 2 ही परिमेय संख्या दर्शवत आहे. म्हणजेच आता OA ची लांबी 2 आहे.
उदाहरण 4:
\sqrt{5} ही संख्या संख्यारेषेवर दर्शवायची असेल तर … ते तर आता अजूनच सोपं झालं आहे.
- आता आपल्याला वरील \sqrt{4} साठीच्या संख्यारेषेवर A ह्या बिंदूवर लंब काढायचा आहे. इथे लक्षात घ्या की OA = 2 आहे.
- ह्या लंबावर B हा एक बिंदू असा घ्या की AB = 1.
- आता O आणि B हे बिंदू एका रेषेने जोडून OAB हा काटकोन त्रिकोण तयार करा.

- आता आपण पायथॅगोरसचा सिद्धांत वापरून त्रिकोण OAB च्या कर्णाची, म्हणजेच बाजू OB ची लांबी काढूयात,
\begin{aligned} \\ (OB)^{2}&=(OA)^{2} + (AB)^{2} \\ &=(2)^{2} + (1)^{2} \\ &=4 + 1 \\ &=\sqrt{5} \end{aligned}
- आता सगळ्यात महत्वाचे: आता \sqrt{5} ही अपरिमेय संख्या संख्यारेषेवर दर्शविण्यासाठी आपण बिंदू O हे केंद्र आणि OB ही त्रिज्या घेऊन एक वर्तुळ काढूया. हे वर्तुळ संख्यारेषेला शून्याच्या उजवीकडे जेथे छेदते ती \sqrt{5} ही संख्या आहे आणि शून्याच्या डावीकडे जिथे छेदते ती \sqrt{5} ही संख्या आहे.
परिमेय संख्यांतील लहानमोठेपणा
हे कायम लक्षात ठेवायचं: संख्यारेषेवर डावीकडील संख्या ह्या उजवीकडील संख्यांपेक्षा लहान असतात.
उदाहरणार्थ:
- 3<5
- -1<0
- -5<-2
- \frac{-2}{3}<\frac{4}{3}
- \frac{-8}{3}<\frac{-2}{3}
आपण आधी काही नियम पाहू,
समजा दोन परिमेय संख्या \mathbf{\left(\frac{a}{b}\right)} आणि \mathbf{\left(\frac{c}{d}\right)} ह्या स्वरूपात असतील तर,
- जर \mathbf{(a \times d)<(b \times c)} तर \mathbf{\left(\frac{a}{b}\right)<\left(\frac{c}{d}\right)}
- जर \mathbf{(a \times d)=(b \times c)} तर \mathbf{\left(\frac{a}{b}\right)=\left(\frac{c}{d}\right)}
- जर \mathbf{(a \times d)>(b \times c)} तर \mathbf{\left(\frac{a}{b}\right)>\left(\frac{c}{d}\right)}
- आपण जेंव्हा एकाच शून्येतर (≠ 0) संख्येने परिमेय संख्येच्या अंश आणि छेदाला (भाजकाला) गुणले तर ती परिमेय संख्या बदलत नाही किंवा तिची किंमत तीच राहते.
\begin{aligned} \\ \therefore \frac{5}{4}&=\frac{5 \times 3}{4 \times 3} \\ &= \frac{15}{12} \end{aligned}
आता आपण वरील नियम वापरून काही उदाहरणं सोडवूयात,
| उदाहरण 1: \frac{5}{4} आणि \frac{7}{3} ह्या मधील मोठी परिमेय संख्या कोणती? उत्तर: इथे a = 5, b = 4, c = 7 आणि d = 3 \begin{aligned} \\ &(a \times d)=(5 \times 3)=15 \\ &(b \times c)=(4 \times 7)=28 \\ &\therefore (a \times d)<(b \times c)\end{aligned} नियम 1 प्रमाणे … \therefore \left(\frac{5}{4}\right)<\left(\frac{7}{3}\right) \therefore \frac{7}{3} ही मोठी परिमेय संख्या आहे. | उदाहरण 3: \frac{8}{3} आणि \frac{5}{4} ह्या मधील मोठी परिमेय संख्या कोणती? उत्तर: इथे a = 8, b = 3, c = 5 आणि d = 4 \begin{aligned} \\ &(a \times d)=(8 \times 4)=32 \\ &(b \times c)=(3 \times 5)=15 \\ &\therefore (a \times d) > (b \times c)\end{aligned} नियम 3 प्रमाणे … \begin{aligned} \\ &\therefore \left(\frac{8} {3}\right)>\left(\frac{5}{4}\right)\end{aligned} \therefore \frac{8}{3} ही मोठी परिमेय संख्या आहे. |
| उदाहरण 2: \frac{8}{2} आणि \frac{16}{4} ह्या मधील मोठी परिमेय संख्या कोणती? उत्तर: इथे a = 8, b = 2, c = 16 आणि d = 4 \begin{aligned} \\ &(a \times d)=(8 \times 4)=32 \\ &(b \times c)=(16 \times 2)=32\end{aligned} \therefore (a \times d)=(b \times c) नियम 2 प्रमाणे … \therefore \left(\frac{8}{2}\right)=\left(\frac{16}{4}\right) \therefore \frac{8}{2} आणि \frac{16}{4} ह्या दोन्ही परिमेय संख्या समान आहेत. | उदाहरण 4: \frac{8}{3} आणि \frac{5}{4} ह्या मधील मोठी परिमेय संख्या कोणती? उत्तर: \frac{8 \times 4}{3 \times 4}=\frac{32}{12} आणि \frac{5 \times 3}{4 \times 3}=\frac{15}{12} (नियम 4 प्रमाणे एकाच शून्येतर (≠ 0) संख्येने परिमेय संख्येच्या अंश आणि छेदाला (भाजकाला) गुणले तर ती परिमेय संख्या बदलत नाही किंवा तिची किंमत तीच राहते.) (a \times d)=(32 \times 12)=384 (b \times c)=(12 \times 15)=180 \therefore (a \times d)>(b \times c) (नियम 3 प्रमाणे) \therefore \frac{32}{12}>\frac{15}{12} \therefore \frac{8}{3} ही परिमेय मोठी संख्या आहे. |
परिमेय संख्यांचे दशांश रूप
परिमेय संख्येतल्या छेदाने (भाजकाने) अंशला भागले की जे उत्तर मिळते ते त्या परिमेय संख्येचे दशांश रूप असते. आता आपण काही उदाहरणं पाहू आणि त्यांची उत्तरं परिमेय संख्येच्या व्याख्येशी पडताळून बघुयात.
उदाहरण 1:
संख्या आहे \frac{5}{4}. आता 4 ने 5 ला भागायचे.
\frac{5}{4}=1.25
ह्याचा अर्थ 4 ने 5 ला पूर्ण भाग जातो (म्हणजे त्यापुढे भागाकाराची क्रिया पुढे चालू ठेवता येत नाही) आणि 1.25 हे खंडित (किंवा मर्यादित) आणि आवर्ती नसलेले भागाकाराचे उत्तर मिळते. खंडित (किंवा मर्यादित) आणि आवर्ती नसलेली संख्या ही परिमेय संख्या असते. ह्याचा अर्थ 1.25 हे \frac{5}{4} ह्या परिमेय संख्येचं दशांश रूप आहे.
उदाहरण 2:
संख्या आहे \frac{7}{6} . आता 6 ने 7 ला भागायचे.
\frac{7}{6} = 1.166666 . . .
ह्या उदाहरणात 6 ने 7 ला कितीही वेळा भागले तरी प्रत्येक वेळी बाकी 40 येते आणि भागाकार 6 येत राहतो. ह्याचा अर्थ 6 ने 7 ला पूर्ण भाग जात नाही आणि भागाकाराची क्रिया ही अखंडित (किंवा अमर्याद) स्वरूपाची असते. इथे भागाकाराचे उत्तर 1.16666 . . . असे अखंडित आणि आवर्ती स्वरूपाचे आहे, हे लक्षात घ्या. असे उत्तर आवर्ती संख्येच्या डोक्यावर एका बिंदूने दर्शविण्याची गणितात पद्धत आहे.
\frac{7}{6} = 1.1\dot{6}
परिमेय संख्यांच्या व्याख्येनुसार कोणतीही अखंडित (किंवा अमर्याद) आणि आवर्ती संख्या ही परिमेय संख्या असते आणि म्हणून 1.16666 . . . हे \frac{7}{6} ह्या परिमेय संख्येचं दशांश रूप आहे.
तर मित्रांनो ही होती परिमेय आणि अपरिमेय संख्यांची ओळख. ह्या प्रकरणात आपण खालील गोष्टींचा अभ्यास केला,
- परिमेय संख्या म्हणजे काय आणि अपरिमेय संख्या म्हणजे काय आणि त्यांच्या व्याख्या काय आहेत.
- परिमेय आणि अपरिमेय संख्यांमधला फरक काय असतो.
- परिमेय आणि अपरिमेय संख्या संख्यारेषेवर कशा दर्शवतात.
- परिमेय संख्यांमधला लहानमोठेपणा कसा ओळखायचा.
- परिमेय संख्या दशांश रूपात कशा दर्शवता येतात.
इयत्ता 8 वीचे पाठयपुस्तक: इथे क्लिक करा
