इयत्ता 8 वी क्षेत्रफळ सूत्र काय आहेत?

इयत्ता 8 वी क्षेत्रफळ सूत्र काय आहेत? : क्षेत्रफळ ही भौमितिक गणितातील एक महत्वाची संकल्पना आहे. एखाद्या पृष्ठभागाची व्याप्ती व्यक्त करायला आपण क्षेत्रफळ ही संकल्पना वापरतो. प्रचलित बोली भाषेत आपण क्षेत्रफळसाठी इंग्रजी “एरिया” हा शब्द वापरतो. एखाद्या भूखंडाची (प्लॉटची) एरिया किती आहे किंवा एखाद्या सदनिकेची (फ्लॅटची) ची एरिया किती आहे, असा प्रश्न आपण रोजच्या व्यवहारात विचारत असतो. ह्या वरून आपल्याला त्या भूखंडाचा किंवा सदनिकेचा आकार (किंवा व्याप्ती) साधारण केवढा आहे, ह्याचा अंदाज येतो.

आपण आता विविध भौमितिक आकारांचे किंवा आकृत्यांचे क्षेत्रफळ कसे काढायचे ते शिकणार आहोत.

Go to top

चौरसाचे क्षेत्रफळ सूत्र

इयत्ता 8 वी साठी क्षेत्रफळ म्हणजे काय? हे समजून घेण्यासाठी आपण चौरसाच्या क्षेत्रफळ सूत्राचा अभ्यास करूया,

आपल्याला माहित आहे की चौरसाच्या चारही बाजूंची लांबी सामान असते आणि म्हणून चौरसाच्या क्षेत्रफळाचं सूत्र आहे,
A=(बाजू)^2
उदाहरण:
एका चौरसाच्या बाजूची लांबी 5 सेमी आहे तर त्या चौरसाचे क्षेत्रफळ किती?
उत्तर:
चौरसाचे क्षेत्रफळ सूत्र A=(बाजू)^2
\therefore A=5\times 5=25 चौरस सेमी.

Go to top

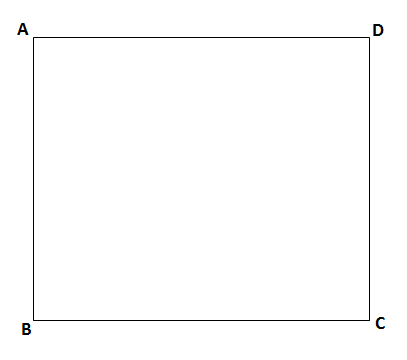
आयताचे क्षेत्रफळ सूत्र

इयत्ता 8 वी साठी क्षेत्रफळ म्हणजे काय? हे समजून घेण्यासाठी आपण आयताच्या क्षेत्रफळ सूत्राचा अभ्यास करूया,

आपल्याला माहित आहे की आयताच्या समोरासमोरील बाजू समान लांबीच्या असतात आणि म्हणून आयताच्या क्षेत्रफळाचं सूत्र आहे,
A= (लांबी) \times (रुंदी)
उदाहरण:
एका आयताच्या एका समोरासमोरील बाजूच्या जोडीतील प्रत्येक बाजूची लांबी 5 सेमी आहे आणि दुसऱ्या समोरासमोरील बाजूच्या जोडीतील प्रत्येक बाजूची लांबी 8 सेमी आहे, तर त्या आयताचे क्षेत्रफळ काढा.
उत्तर:
आयताचे क्षेत्रफळ सूत्र A= (लांबी) \times (रुंदी)
\therefore A=5\times 8=40 चौरस सेमी.

Go to top

त्रिकोणाचे क्षेत्रफळ सूत्र

इयत्ता 8 वी साठी क्षेत्रफळ म्हणजे काय? हे समजून घेण्यासाठी आपण त्रिकोणाच्या क्षेत्रफळ सूत्राचा अभ्यास करूया,

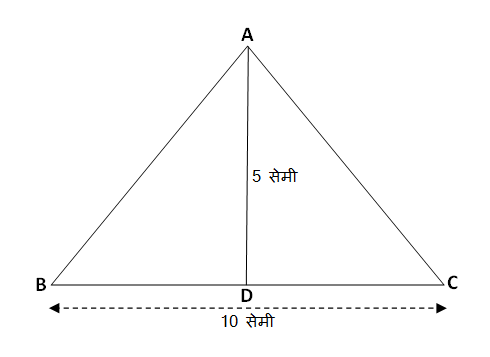
शेजारील आकृतीत \triangle ABC दिलेला आहे. रेख AD हा शिरोबिंदू A मधून त्रिकोणाचा पाया BC वर टाकलेला लंब आहे. रेख AD ची लांबी ही त्या त्रिकोणाची उंची असते. म्हणून त्रिकोणाचे क्षेत्रफळ सूत्र आहे,
\frac{1}{2}\times (पाया) \times (उंची)

उदाहरण:
\triangle ABC च्या पायाची लांबी 10 सेमी असून उंची 5 सेमी आहे, तर \triangle ABC चं क्षेत्रफळ काढा.

उत्तर:
त्रिकोणाचं क्षेत्रफळ A=\frac{1}{2}\times (पाया) \times (उंची)
\begin{aligned} \\ &\therefore A=\frac{1}{2}\times \ell\left(BC\right)\times \ell\left(AD\right) \\ &\therefore A=\frac{1}{2}\times 10\times 5 \\ &\therefore A=\frac{1}{2}\times 50 \\ &\therefore A=25\end{aligned}
\therefore \triangle ABC चं क्षेत्रफळ 25 चौरस सेमी आहे.

Go to top

काटकोन त्रिकोणाचे क्षेत्रफळ सूत्र

इयत्ता 8 वी साठी क्षेत्रफळ म्हणजे काय? हे समजून घेण्यासाठी आपण काटकोन त्रिकोणाच्या क्षेत्रफळ सूत्राचा अभ्यास करूया,

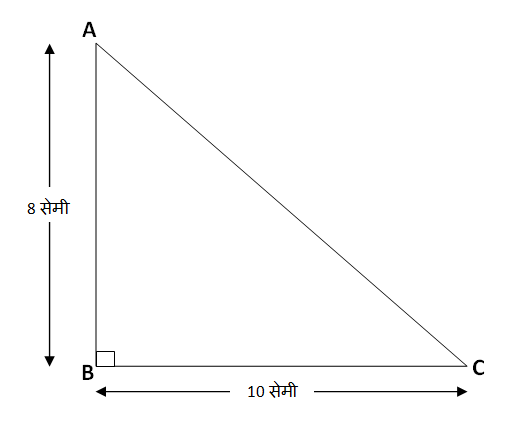
शेजारील आकृतीत \triangle ABC काटकोन त्रिकोण दिलेला आहे. काटकोन त्रिकोणाच्या क्षेत्रफळाचं सूत्र आहे,
\frac{1}{2}\times (काटकोन करणाऱ्या बाजूंचा गुणाकार)
उदाहरण:
\triangle ABC काटकोन करणाऱ्या एका बाजूची लांबी 10 सेमी तर दुसऱ्या बाजूची लांबी 8 सेमी आहे; तर त्या काटकोन त्रिकोणाचे क्षेत्रफळ काढा.
उत्तर:
काटकोन त्रिकोणाचं क्षेत्रफळ \frac{1}{2}\times (काटकोन करणाऱ्या बाजूंचा गुणाकार)
\begin{aligned} \\ &\therefore A=\frac{1}{2}\times \ell\left(BC\right)\times \ell\left(AB\right) \\ &\therefore A=\frac{1}{2}\times 10\times 8 \\ &\therefore A=\frac{1}{2}\times 80 \\ &\therefore A=40\end{aligned}
\therefore \triangle ABC चं क्षेत्रफळ 40 चौरस सेमी आहे.

Go to top

समांतरभुज चौकोनाचे क्षेत्रफळ सूत्र

इयत्ता 8 वी साठी क्षेत्रफळ म्हणजे काय? हे समजून घेण्यासाठी आपण समांतरभुज चौकोनाच्या क्षेत्रफळ सूत्राचा अभ्यास करूया,

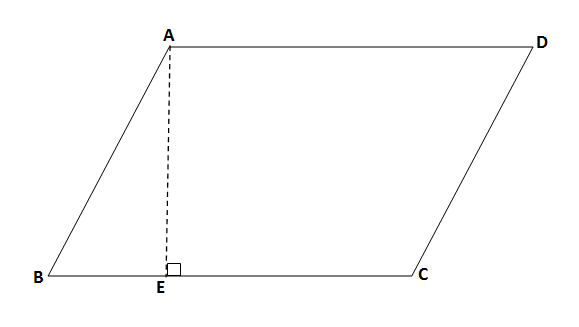
शेजारील आकृतीत \square ABCD हा समांतरभुज चौकोन दिलेला आहे.

शेजारील समांतरभुज चौकोनाच्या आकृतीत आपण पुढील बदल करूया,
1) समांतरभुज \square ABCD मधून \triangle ABE हा रेख AE वर कापून बाजूला काढा.
2) आता \square AECD ची बाजू CD आणि कापलेल्या \triangle ABE ची बाजू AB जुळवा.
3) अशाप्रकारे \square AECD आणि \triangle ABE जुळवले की तुमच्या लक्षात येईल की आपल्याला आयत \square AEED मिळतो.
4) ह्याचा अर्थ समांतरभुज \square ABCD आणि आयत \square AEED ह्यांचं क्षेत्रफळ समान आहे. त्यामुळे समांतरभुज चौकोन आणि आयत ह्यांच्या क्षेत्रफळाचं सूत्र देखील समान आहे.
5) आयताच्या क्षेत्रफळाचं सूत्र आहे
A= (लांबी) \times (रुंदी)
तर समांतरभुज चौकोनाच्या क्षेत्रफळाचं सूत्र आहे,
\mathbf{A=} (पाया) \mathbf{\times} (उंची)
इथे पाया = बाजू BC आणि उंची = बाजू AE.

इयत्ता 8 वी साठी क्षेत्रफळ म्हणजे काय? हे समजून घेण्यासाठी आपण समांतरभुज चौकोनाच्या क्षेत्रफळाची काही उदाहरणे सोडवुया,

उदा 1:
एका समांतरभुज चौकोनाच्या पाया 8 सेमी आणि उंची 5 सेमी असेल तर त्या समांतरभुज चौकोनाचे क्षेत्रफळ काढा.
उत्तर:
आधी उदाहरणात काय दिलेलं आहे, ते लिहून घेऊ,
पाया = 8 सेमी
उंची = 5 सेमी
समांतरभुज चौकोनाचे क्षेत्रफळ सूत्र आहे,
\mathbf{A=} (पाया) \mathbf{\times} (उंची)
\begin{aligned} \\ &\therefore A=8\times 5 \\ &\therefore A=40\end{aligned}
म्हणून समांतरभुज चौकोनाचं क्षेत्रफळ 40 चौरस सेमी आहे.

उदा 2:
एका समांतरभुज चौकोनाचे क्षेत्रफळ 112 चौसेमी असून त्याचा पाया 10 सेमी असेल तर त्याची उंची काढा.
उत्तर:
आधी उदाहरणात काय दिलेलं आहे, ते लिहून घेऊ,
क्षेत्रफळ A = 112 चौसेमी
पाया b = 10 सेमी
उंची h = ?
समांतरभुज चौकोनाच्या क्षेत्रफळाचं सूत्र आहे,
\mathbf{A=} (पाया) \mathbf{\times} (उंची)
\begin{aligned} \\ &\therefore A=b\times h \\ &\therefore 112=10\times h \\ &\therefore h=\frac{112}{10} \\ &\therefore h=11.2\end{aligned}
म्हणून समांतरभुज चौकोनाची उंची 11.2 सेमी आहे.

उदा 3:
एका समांतरभुज चौकोनाच्या पाया 18 सेमी आणि उंची 11 सेमी असेल तर त्या समांतरभुज चौकोनाचे क्षेत्रफळ काढा.
उत्तर:
आधी उदाहरणात काय दिलेलं आहे, ते लिहून घेऊ,
पाया = 18 सेमी
उंची = 11 सेमी
समांतरभुज चौकोनाचे क्षेत्रफळ सूत्र आहे,
\mathbf{A=} (पाया) \mathbf{\times} (उंची)
\begin{aligned} \\ &\therefore A=18\times 11 \\ &\therefore A=198\end{aligned}
म्हणून समांतरभुज चौकोनाचं क्षेत्रफळ 198 चौरस सेमी आहे.

उदा 4:
एका समांतरभुज चौकोनाचे क्षेत्रफळ 29.6 चौसेमी असून त्याचा पाया 8 सेमी असेल तर त्याची उंची काढा.
उत्तर:
आधी उदाहरणात काय दिलेलं आहे, ते लिहून घेऊ,
क्षेत्रफळ A = 29.6 चौसेमी
पाया b = 8 सेमी
उंची h = ?
समांतरभुज चौकोनाच्या क्षेत्रफळाचं सूत्र आहे,
\mathbf{A=} (पाया) \mathbf{\times} (उंची)
\begin{aligned} \\ &\therefore A=b\times h \\ &\therefore 29.6=8\times h \\ &\therefore h=\frac{29.6}{8} \\ &\therefore h=3.7\end{aligned}
म्हणून समांतरभुज चौकोनाची उंची 3.7 सेमी आहे.

उदा 5:
एका समांतरभुज चौकोनाचे क्षेत्रफळ 83.2 चौसेमी असून त्याची उंची 6.4 सेमी आहे तर त्याचा पाया काढा.
उत्तर:
आधी उदाहरणात काय दिलेलं आहे, ते लिहून घेऊ,
क्षेत्रफळ A = 83.2 चौसेमी
उंची h = 6.4 सेमी
पाया b = ?
समांतरभुज चौकोनाचे क्षेत्रफळ सूत्र आहे,
\mathbf{A=} (पाया) \mathbf{\times} (उंची)
\begin{aligned} \\ &\therefore A=b\times h \\ &\therefore 83.2=b\times 6.4 \\ &\therefore b=\frac{83.2}{6.4} \\ &\therefore b=13\end{aligned}
म्हणून समांतरभुज चौकोचा पाया 13 सेमी आहे.

Go to top

समभुज चौकोनाचे क्षेत्रफळ सूत्र

इयत्ता 8 वी साठी क्षेत्रफळ म्हणजे काय? हे समजून घेण्यासाठी आपण समभुज चौकोनाच्या क्षेत्रफळ सूत्राचा अभ्यास करूया,

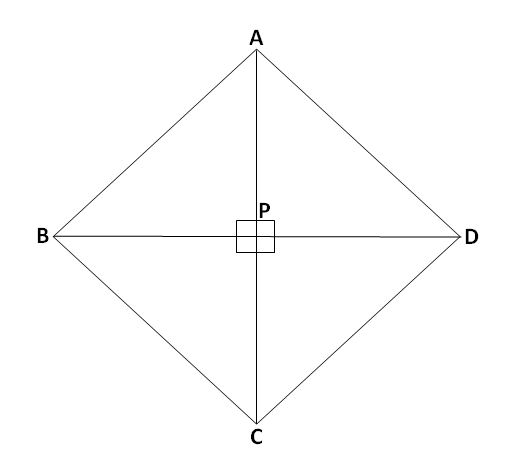
शेजारील आकृतीत \square ABCD समभुज चौकोन आहे. समभुज चौकोनाचे कर्ण एकमेकांना त्यांच्या मध्य बिंदूत काटकोनात छेदतात. म्हणजेच समभुज चौकोनाचे कर्ण हे परस्परांचे लंब दुभाजक असतात. समभुज चौकोनाच्या कर्णांच्या ह्या रचनेमुळे आपल्याला चार एकरूप काटकोन त्रिकोण मिळतात.
\begin{aligned} \\ &(1) \triangle APB \\ &(2) \triangle APD \\ &(3) \triangle CPB \\&(4) \triangle CPD\end{aligned}
हे ते चार काटकोन त्रिकोण आहेत. म्हणून ह्या चार काटकोन त्रिकोणांच्या क्षेत्रफळांची बेरीज म्हणजे समभुज चौकोनाचे क्षेत्रफळ असते.
आपल्याला काटकोन त्रिकोणाच्या क्षेत्रफळाचे सूत्र आधीच माहित आहे,
A=\frac{1}{2}\times (काटकोन करणाऱ्या बाजूंचा गुणाकार)
म्हणून समभुज चौकोनाचे क्षेत्रफळ सूत्र A=4\times (काटकोन त्रिकोणाचे क्षेत्रफळ)

\begin{aligned}\therefore A=&\left(\frac{1}{2}\times \ell\left(AP\right)\times \ell\left(BP\right)\right)+\left(\frac{1}{2}\times \ell\left(BP\right)\times \ell\left(CP\right)\right)+ \\ &\left(\frac{1}{2}\times \ell\left(CP\right)\times \ell\left(DP\right)\right)+\left(\frac{1}{2}\times \ell\left(DP\right)\times \ell\left(AP\right)\right) \\ \therefore A=&4\times \left(\frac{1}{2}\times \ell\left(AP\right)\times \ell\left(BP\right)\right)\end{aligned}

पण \ell\left(AP\right)=\frac{1}{2}\times \ell\left(AC\right) आणि \ell\left(BP\right)=\frac{1}{2}\times \ell\left(BD\right)

\begin{aligned}\therefore A=&\;4\times \left(\frac{1}{2}\times \left(\frac{1}{2}\times \ell\left(AC\right)\times \frac{1}{2}\times \ell\left(BD\right)\right)\right) \\ \therefore A=&\;4\times \left(\frac{1}{8}\times \ell\left(AC\right)\times \ell\left(BD\right)\right) \\ \therefore A=&\;\frac{1}{2}\times \ell\left(AC\right)\times \ell\left(BD\right)\end{aligned}

पण रेख AC आणि रेख BD हे समभुज चौकोनाचे कर्ण आहेत.

\therefore \mathbf{A=\frac{1}{2}\times } (समभुज चौकोनाच्या कर्णांच्या लांबीचा गुणाकार)

इयत्ता 8 वी साठी क्षेत्रफळ म्हणजे काय? हे समजून घेण्यासाठी आपण समभुज चौकोनाच्या क्षेत्रफळाची काही उदाहरणे सोडवुया,

उदा 1:
एका समभुज चौकोनाच्या दोन कर्णांची लांबी अनुक्रमे 11.2 सेमी व 7.5 सेमी आहे तर त्या चौकोनाचे क्षेत्रफळ काढा.
उत्तर:
आधी उदाहरणात काय दिलेलं आहे, ते लिहून घेऊ,
एका कर्णाची लांबी = 11.2 सेमी
दुसऱ्या कर्णाची लांबी = 7.5 सेमी
समभुज चौकोनाचे क्षेत्रफळ सूत्र A=\frac{1}{2}\times (समभुज चौकोनाच्या कर्णांच्या लांबीचा गुणाकार)
\begin{aligned} \\ &\therefore A=\frac{1}{2}\times \left(11.2\right)\times \left(7.5\right) \\ &\therefore A=\frac{1}{2}\times \left(84\right) \\ &\therefore A=42\end{aligned}
म्हणून समभुज चौकोनाचे क्षेत्रफळ 42 चौरस सेमी आहे.

उदा 2:
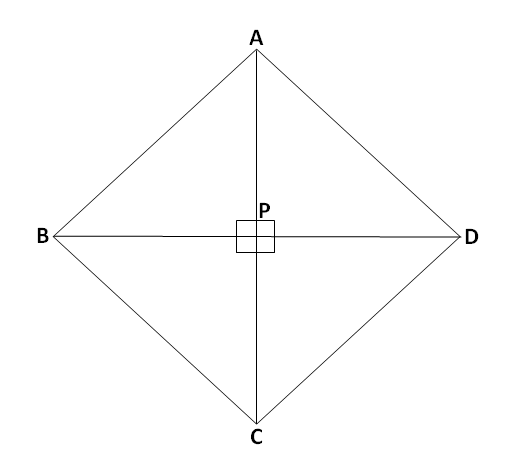
एका समभुज चौकोनाचे क्षेत्रफळ 96 चौरस सेमी आहे. त्याचा एक कर्ण 12 सेमी आहे तर त्या चौकोनाच्या बाजूची लांबी काढा.

उत्तर:
आधी उदाहरणात काय दिलेलं आहे, ते लिहून घेऊ,
क्षेत्रफळ A = 96 चौरस सेमी
एका कर्णाची लांबी \ell\left(AC\right)=12 सेमी
दुसऱ्या कर्णाची लांबी = \ell\left(BD\right)=x सेमी मानू.

इथे लक्षात घ्या की आपल्याला समभुज चौकोनाच्या बाजूची लांबी काढायची आहे. त्यासाठी आपल्याला प्रथम दिलेल्या माहितीवरून त्या समभुज चौकोनाच्या दुसऱ्या कर्णाची लांबी काढावी लागेल आणि नंरत दोन्ही कर्णांच्या लांबीच्या आधारे पायथॅगोरसचं सूत्र वापरून त्या समभुज चौकोनाच्या बाजूची लांबी काढावी लागेल.

समभुज चौकोनाचे क्षेत्रफळ सूत्र A=\frac{1}{2}\times (समभुज चौकोनाच्या कर्णांच्या लांबीचा गुणाकार)
\begin{aligned} \\ &\therefore 96=\frac{1}{2}\times \left(12\right)\times \left(x\right) \\ &\therefore 96=\frac{12x}{2} \\ &\therefore 96=6x \\ &\therefore x=\frac{96}{6} \\ &\therefore x=16\end{aligned}
म्हणून समभुज चौकोनाच्या दुसऱ्या कर्णाची लांबी 16 सेमी आहे.

आपल्याला माहित आहे की समभुज चौकोनाचे कर्ण परस्परांना त्यांच्या मध्यबिंदूत काटकोनात छेदतात आणि त्यामुळे ह्या दोन्ही कर्णांची दोन सामान रेषाखंडांत खालील प्रमाणे विभागणी होते,
\begin{aligned} \\ &\therefore \ell\left(AP\right)=\frac{1}{2}\times \ell\left(AC\right) \\ &\therefore \ell\left(AP\right)=\frac{1}{2}\times 16 \\ &\therefore \ell\left(AP\right)=8\end{aligned}

\begin{aligned} \\ &\therefore \ell\left(BP\right)=\frac{1}{2}\times \ell\left(BD\right) \\ &\therefore \ell\left(BP\right)=\frac{1}{2}\times 12 \\ &\therefore \ell\left(BP\right)=6\end{aligned}

आता पायथॅगोरसचं सूत्र वापरून आपण दिलेल्या समभुज चौकोनाच्या बाजूची लांबी काढूया,
\begin{aligned} \\ &\therefore \ell\left(AB\right)^2=\ell\left(AP\right)^2+\ell\left(BC\right)^2 \\ &\therefore \ell\left(AB\right)^2=\left(8\right)^2+\left(6\right)^2 \\ &\therefore \ell\left(AB\right)^2=64+36 \\ &\therefore \ell\left(AB\right)^2=100 \\ &\therefore \sqrt{\ell\left(AB\right)^2}=\sqrt{100} \\ &\therefore \ell\left(AB\right)=10\end{aligned}

उदा 3:
एका समभुज चौकोनाच्या दोन कर्णांची लांबी प्रत्येकी 15 सेमी व 24 सेमी आहे, तर त्याचे क्षेत्रफळ काढा.
उत्तर:
आधी उदाहरणात काय दिलेलं आहे, ते लिहून घेऊ,
एका कर्णाची लांबी = 15 सेमी
दुसऱ्या कर्णाची लांबी = 24 सेमी
समभुज चौकोनाचे क्षेत्रफळ सूत्र A=\frac{1}{2}\times (समभुज चौकोनाच्या कर्णांच्या लांबीचा गुणाकार)
\begin{aligned} \\ &\therefore A=\frac{1}{2}\times \left(15\right)\times \left(24\right) \\ &\therefore A=\frac{1}{2}\times \left(360\right) \\ &\therefore A=180\end{aligned}
म्हणून समभुज चौकोनाचे क्षेत्रफळ 180 चौरस सेमी आहे.

उदा 4:
एका समभुज चौकोनाच्या दोन कर्णांची लांबी अनुक्रमे 16.5 सेमी व 14.2 सेमी आहे, तर त्या समभुज चौकोनाचे क्षेत्रफळ काढा.
उत्तर:
आधी उदाहरणात काय दिलेलं आहे, ते लिहून घेऊ,
एका कर्णाची लांबी = 16.5 सेमी
दुसऱ्या कर्णाची लांबी = 14.2 सेमी
समभुज चौकोनाचं क्षेत्रफळ A=\frac{1}{2}\times (समभुज चौकोनाच्या कर्णांच्या लांबीचा गुणाकार)
\begin{aligned} \\ &\therefore A=\frac{1}{2}\times \left(16.5\right)\times \left(14.2\right) \\ &\therefore A=\frac{1}{2}\times \left(234.3\right) \\ &\therefore A=117.15\end{aligned}
म्हणून समभुज चौकोनाचे क्षेत्रफळ 117.15 चौरस सेमी आहे.

उदा 5:
एका समभुज चौकोनाचा एक कर्ण 30 सेमी असून त्याचे क्षेत्रफळ 240 चौसेमी आहे. तर त्या चौकोनाची परिमिती काढा.

उत्तर:
आधी उदाहरणात काय दिलेलं आहे, ते लिहून घेऊ,
एका कर्णाची लांबी \ell\left(AC\right)= 48 सेमी
परिमिती =100 सेमी

समभुज चौकोनाची परिमिती = (समभुज चौकोनाच्या चारही बाजूंच्या लांबीची बेरीज) = 4\times (समभुज चौकोनाच्या एका बाजूची लांबी)

समभुज चौकोनाच्या बाजूची लांबी = (समभुज चौकोनाची परिमिती) / 4
\begin{aligned}\therefore \ell\left(AB\right)=\ell\left(BC\right)=\ell\left(CD\right)=\ell\left(DA\right)=\frac{100}{4}=25\end{aligned}

आपल्याला आता \square ABCD च्या बाजूची लांबी आणि एका कर्णाची लांबी माहित आहे. \square ABCD चं क्षेत्रफळ काढण्यासाठी आपल्याला त्या चौकोनाच्या दुसऱ्या कर्णाची लांबी काढावी लागणार आहे आणि त्यासाठी आपल्याला \triangle ABC हा काटकोन त्रिकोण विचारात घ्यावा लागणार आहे आणि पायथागोरसचं सूत्र वापरून ह्या त्रिकोणाच्या काटकोन करणाऱ्या बाजूची लांबी काढावी लागणार आहे आणि त्यावरून आपल्याला \triangle ABC च्या दुसऱ्या कर्णाची लांबी मिळेल.

\begin{aligned} \\ &\therefore \ell\left(AP\right)=\frac{1}{2}\times \ell\left(AC\right) \\ &\therefore \ell\left(AP\right)=\frac{1}{2}\times \left(48\right) \\ &\therefore \ell\left(AP\right)=24\end{aligned}

आता पायथॅगोरसचं सूत्र वापरून आपण \triangle ABC च्या बाजू BP ची लांबी काढूया त्यासाठी बाजू BP ची लांबी x मानू,
\begin{aligned} \\ &\therefore \ell\left(AB\right)^2=\ell\left(AP\right)^2+\ell\left(BP\right)^2 \\ &\therefore \left(25\right)^2=\left(24\right)^2+\left(x\right)^2 \\ &\therefore \left(x\right)^2=\left(25\right)^2-\left(24\right)^2 \\ &\therefore \left(x\right)^2=\left(625\right)-\left(576\right) \\ &\therefore x^2=49 \\ &\therefore \sqrt{\left(x\right)^2}=\sqrt{49} \\ &\therefore x=7 \\ &\therefore \ell\left(BP\right)=7\end{aligned}

\therefore \square ABCD च्या दुसऱ्या कर्णाची लांबी पुढील प्रमाणे काढावी लागेल,
\begin{aligned} \\ &\therefore \ell\left(BD\right)=2\times \ell\left(BP\right) \\ &\therefore \ell\left(BD\right)=2\times 7 \\ &\therefore \ell\left(BD\right)=14\end{aligned}

समभुज चौकोनाचं क्षेत्रफळ A=\frac{1}{2}\times (समभुज चौकोनाच्या कर्णांच्या लांबीचा गुणाकार)
\begin{aligned} \\ &\therefore A=\frac{1}{2}\times \ell\left(AC\right)\times \ell\left(BD\right) \\ &\therefore A=\frac{1}{2}\times \left(48\right)\times \left(14\right) \\ &\therefore A=\frac{1}{2}\times \left(672\right) \\ &\therefore A=336\end{aligned}
म्हणून समभुज चौकोनाचे क्षेत्रफळ 336 चौरस सेमी आहे.

उदा 6:

एका समभुज चौकोनाचा एक कर्ण 30 सेमी असून त्याचे क्षेत्रफळ 240 चौसेमी आहे. तर त्या चौकोनाची परिमिती काढा.

उत्तर:
आधी उदाहरणात काय दिलेलं आहे, ते लिहून घेऊ,
एका कर्णाची लांबी \ell\left(AC\right)=30 सेमी
क्षेत्रफळ A=240 चौसेमी
परिमिती = ?

1. ह्या उदाहरणात आपल्याला समभुज चौकोनाची परिमिती काढायची आहे. समभुज चौकोनाची परिमिती म्हणजे त्या चौकोनाच्या चारही बाजूंच्या लांबीची बेरीज असते. त्यामुळे आपल्याला आधी दिलेल्या माहितीवरून ह्या समभुज चौकोनाच्या एका बाजूची लांबी काढावी लागणार आहे.
2. वर दिलेल्या आकृतीत \square ABCD मध्ये \triangle APB हा काटकोन त्रिकोण समाविष्ट आहे.
3. \square ABCD ची बाजू AB ही \triangle APB चा कर्ण आहे, हे लक्षात घ्या.
4. त्यामुळे \square ABCD च्या बाजू AB ची लांबी काढण्यासाठी आपल्याला \triangle APB साठी पायथॅगोरसचे सूत्र वापरून कर्ण AB ची लांबी काढावी लागणार आहे.
5. आपल्याला \square ABCD च्या कर्ण AC ची लांबी माहित आहे; त्यावरून आपण \triangle APB च्या बाजू AP ची लांबी काढू शकतो.
6. \triangle APB ची बाजू BP ही \square ABCD चा दुसरा कर्ण BD मध्ये समाविष्ट असल्याने बाजू BP ची लांबी काढण्यासाठी आपल्याला आधी समभुज चौकोनाच्या क्षेत्रफळाचं सूत्र वापरून कर्ण BD ची लांबी काढावी लागणार आहे.

पायरी 1:
आपल्याला माहित आहे की समभुज चौकोनाचे कर्ण परस्परांना त्यांच्या मध्यबिंदूत काटकोनात छेदतात आणि त्यामुळे ह्या दोन्ही कर्णांची दोन सामान रेषाखंडांत विभागणी होते,
\begin{aligned} \\ &\therefore \ell\left(AP\right)=\frac{1}{2}\times \ell\left(AC\right) \\ &\therefore \ell\left(AP\right)=\frac{1}{2}\times 30 \\ &\mathbf{\therefore \ell\left(AP\right)=15}\end{aligned}

पायरी 2:
आता आपण समभुज चौकोनाच्या क्षेत्रफळाचं सूत्र वापरून \square ABCD चा दुसरा कर्ण BD ची लांबी काढूया,
समभुज चौकोनाचं क्षेत्रफळ A=\frac{1}{2}\times (समभुज चौकोनाच्या कर्णांच्या लांबीचा गुणाकार)
\begin{aligned} \\ &\therefore A=\frac{1}{2}\times \ell\left(AC\right)\times \ell\left(BD\right) \\ &\therefore 240=\frac{1}{2}\times \left(30\right)\times \ell\left(BD\right) \\ &\therefore 240\times 2=\left(30\right)\times \ell\left(BD\right) \\ &\therefore 480=\left(30\right)\times \ell\left(BD\right) \\ &\therefore \ell\left(BD\right)=\frac{480}{30} \\ &\therefore \ell\left(BD\right)=16\end{aligned}
म्हणून समभुज चौकोनाच्या दुसऱ्या कर्णाची लांबी 16 सेमी आहे.

आता आपण \square ABCD चा दुसरा कर्ण BD ची लांबी वापरून \triangle ABP च्या दुसऱ्या बाजूची, म्हणजे बाजू BP ची लांबी काढूया,
समभुज चौकोनाचे कर्ण परस्परांना त्यांच्या मध्यबिंदूत काटकोनात छेदतात आणि त्यामुळे ह्या दोन्ही कर्णांची दोन सामान रेषाखंडांत विभागणी होते,
\begin{aligned} \\ &\therefore \ell\left(BP\right)=\frac{1}{2}\times \ell\left(BD\right) \\ &\therefore \ell\left(BP\right)=\frac{1}{2}\times 16 \\ &\mathbf{\therefore \ell\left(BP\right)=8}\end{aligned}

पायरी 3:
आता \triangle APB साठी पायथॅगोरसचं सूत्र वापरून आपण दिलेल्या समभुज चौकोनाच्या बाजूची लांबी काढूया,
\begin{aligned} \\ &\therefore \ell\left(AB\right)^2=\ell\left(AP\right)^2+\ell\left(BP\right)^2 \\ &\therefore \ell\left(AB\right)^2=\left(15\right)^2+\left(8\right)^2 \\ &\therefore \ell\left(AB\right)^2=225+64 \\ &\therefore \ell\left(AB\right)^2=289 \\ &\therefore \sqrt{\ell\left(AB\right)^2}=\sqrt{289} \\ &\mathbf{\therefore \ell\left(AB\right)=17}\end{aligned}

समभुज चौकोनाची परिमिती = (समभुज चौकोनाच्या चारही बाजूंच्या लांबीची बेरीज) = 4\times (समभुज चौकोनाच्या एका बाजूची लांबी)

\begin{aligned} \\ &\therefore P=4\times 17 \\ &\mathbf{\therefore P=68}\end{aligned}
म्हणून समभुज चौकोनाची परिमिती 68 सेमी आहे.

Go to top

समलंब चौकोनाचे क्षेत्रफळ सूत्र

इयत्ता 8 वी साठी क्षेत्रफळ म्हणजे काय? हे समजून घेण्यासाठी आपण समलंब चौकोनाच्या क्षेत्रफळ सूत्राचा अभ्यास करूया,

शेजारच्या आकृतीत \square ABCD दिलेला आहे. रेख AP आणि रेख DQ हे बाजू AD मधून बाजू BC वर टाकलेले लंब आहेत. m\angle APB=m\angle DQC=90^\circ.
रेख AP = रेख DQ असल्याने ह्या चौकोनाला समलंब चौकोन म्हणतात.

रेख AP = रेख DQ = h (उंची)

रेख AP आणि रेख DQ मुळे \square ABCD चे पुढील तीन भाग पडतात,
1) \triangle APB
2) आयत \square APQD
3) \triangle DQC

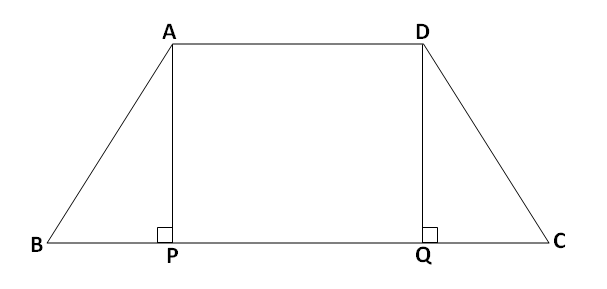
म्हणून समलंब \square ABCD चं क्षेत्रफळ = (\triangle APB चं क्षेत्रफळ) + (आयत \square APQD चं क्षेत्रफळ) + (\triangle DQC चं क्षेत्रफळ)

\begin{aligned} \\ \therefore A\left(\square ABCD\right)&=A\left(\triangle APB\right)+A\left(\square APQD\right)+A\left(\triangle DQC\right) \\ &=\left(\frac{1}{2}\times \ell\left(BP\right)\times h\right)+\left(\ell\left(PQ\right)\times h\right)+\left(\frac{1}{2}\times \ell\left(CQ\right)\times h\right) \\ &=\frac{1}{2}\times \ell\left(BP\right)\times h+\ell\left(PQ\right)\times h+\frac{1}{2}\times \ell\left(CQ\right)\times h \\ &=h\times \left[\frac{1}{2}\times \ell\left(BP\right)+\ell\left(PQ\right)+\frac{1}{2}\times \ell\left(CQ\right)\right] \\ &=\frac{1}{2}\times h\times \left[\ell\left(BP\right)+2\times \ell\left(PQ\right)+\ell\left(CQ\right)\right] \\ &=\frac{1}{2}\times h\times \left[\ell\left(BP\right)+\ell\left(AD\right)+\ell\left(PQ\right)+\ell\left(CQ\right)\right] \\ &=\frac{1}{2}\times h\times \left[\ell\left(BP\right)+\ell\left(PQ\right)+\ell\left(CQ\right)+\ell\left(AD\right)\right] \\ &=\frac{1}{2}\times h\times \left[\ell\left(BC\right)+\ell\left(AD\right)\right]\end{aligned}
\mathbf{\therefore } समलंब चौकोनाचे क्षेत्रफळ सूत्र \mathbf{=\frac{1}{2}\times } (समांतर बाजूंच्या लांबींची बेरीज) \mathbf{\times } उंची

इयत्ता 8 वी साठी क्षेत्रफळ म्हणजे काय? हे समजून घेण्यासाठी आपण समलंब चौकोनाच्या क्षेत्रफळाची काही उदाहरणे सोडवुया,

उदा 1:
एका समलंब चौकोनाच्या संमुख भुजांची एक जोडी परस्परांना समांतर आहे. त्या भुजांमधील अंतर 6 सेमी आहे व समांतर बाजूंची लांबी अनुक्रमे 7 सेमी व 8 सेमी आहे, तर त्या समलंब चौकोनाचे क्षेत्रफळ काढा.
उत्तर:
आधी उदाहरणात काय दिलं आहे, ते लिहून घेऊ,
भुजांमधील अंतर (उंची) h=6 सेमी
एका समांतर बाजूची लांबी =7 सेमी
दुसऱ्या समांतर बाजूची लांबी =8 सेमी
समलंब चौकोनाचे क्षेत्रफळ सूत्र =\frac{1}{2}\times (समांतर बाजूंच्या लांबींची बेरीज) \times उंची
\begin{aligned} \\ &\therefore A=\frac{1}{2}\times \left(7+8\right)\times 6 \\ &\therefore A=\frac{1}{2}\times \left(15\right)\times 6 \\ &\therefore A=\frac{1}{2}\times 90 \\ &\therefore A=45\end{aligned}
\therefore समलंब चौकोनाचे क्षेत्रफळ 45 चौरस सेमी आहे.

उदा 2:
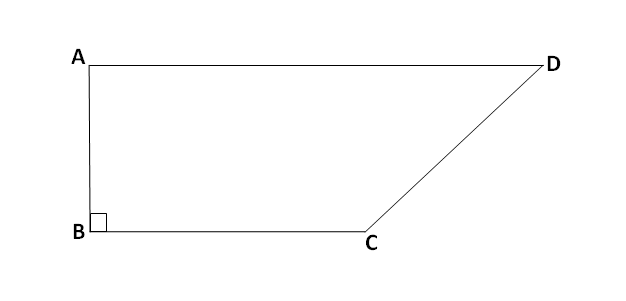
ABCD मध्ये \ell\left(AB\right)=13 सेमी, \ell\left(AD\right)=9 सेमी, \ell\left(BC\right)=8 सेमी, तर ABCD चे क्षेत्रफळ काढा.

उत्तर:
आधी उदाहरणात काय दिलं आहे, ते लिहून घेऊ,
\ell\left(AD\right)=13 सेमी
\ell\left(BC\right)=9 सेमी
\ell\left(AB\right)=8 सेमी
समलंब चौकोनाचे क्षेत्रफळ सूत्र =\frac{1}{2}\times (समांतर बाजूंच्या लांबींची बेरीज) \times उंची
\begin{aligned} \\ &\therefore A=\frac{1}{2}\times \left[\ell\left(AD\right)+\ell\left(BC\right)\right]\times \ell\left(AB\right) \\ &\therefore A=\frac{1}{2}\times \left(13+9\right)\times 8 \\ &\therefore A=\frac{1}{2}\times \left(22\right)\times 8 \\ &\therefore A=\frac{1}{2}\times 176 \\ &\therefore A=88\end{aligned}
\therefore समलंब चौकोनाचे क्षेत्रफळ 88 चौरस सेमी आहे.

उदा 3:
एका समलंब चौकोनाच्या समांतर बाजूंची लांबी अनुक्रमे 8.5 सेमी व 11.5 सेमी आहे. त्याची उंची 4.2 सेमी आहे; तर त्या समलंब चौकोनाचे क्षेत्रफळ काढा.
उत्तर:
आधी उदाहरणात काय दिलं आहे, ते लिहून घेऊ,
एका समांतर बाजूची लांबी =8.5 सेमी
दुसऱ्या समांतर बाजूची लांबी =11.5 सेमी
उंची h=4.2 सेमी

समलंब चौकोनाचे क्षेत्रफळ सूत्र =\frac{1}{2}\times (समांतर बाजूंच्या लांबींची बेरीज) \times उंची
\begin{aligned} \\ &\therefore A=\frac{1}{2}\times \left(8.5+11.5\right)\times 4.2 \\ &\therefore A=\frac{1}{2}\times \left(20\right)\times 4.2 \\ &\therefore A=\frac{1}{2}\times 84 \\ &\therefore A=42\end{aligned}
\therefore समलंब चौकोनाचे क्षेत्रफळ 42 चौरस सेमी आहे.

उदा 4:
\square ABCD हा समद्विभुज समलंब चौकोन आहे. \ell\left(AD\right)=7 सेमी, रेख AP\parallel बाजू BC, \ell\left(BP\right)=3 सेमी, समांतर बाजूंमधील अंतर 4 सेमी आहे, तर \square ABCD चे क्षेत्रफळ काढा.

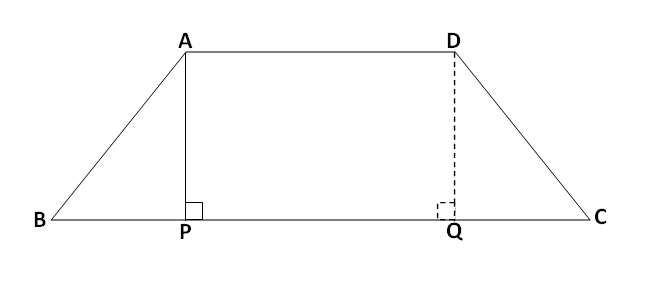
उत्तर:
आधी उदाहरणात काय दिलं आहे, ते लिहून घेऊ,
\ell\left(AD\right)=7 सेमी
\ell\left(BP\right)=3 सेमी
\ell\left(AP\right)=4 सेमी

पायरी 1:
\triangle APB हा काटकोन त्रिकोण आहे. आता आपण \triangle APB साठी पायथॅगोरसचे सूत्र वापरून बाजू AB ची लांबी काढूया,
\begin{aligned} \\ &\therefore \ell\left(AB\right)^2=\ell\left(AP\right)^2+\ell\left(BP\right)^2 \\ &\therefore \ell\left(AB\right)^2=\left(4\right)^2+\left(3\right)^2 \\ &\therefore \ell\left(AB\right)^2=\left(16\right)+\left(9\right) \\ &\therefore \ell\left(AB\right)^2=25 \\ &\therefore \sqrt{\ell\left(AB\right)^2}=\sqrt{25} \\ &\therefore \mathbf{\ell\left(AB\right)=5}\end{aligned}

इथे लक्षात घ्या की दिलेला समलंब चौकोन हा “समद्विभुज” समलंब चौकोन आहे. त्यामुळे \mathbf{\ell\left(AB\right)=\ell\left(CD\right)=5} सेमी

पायरी 2:
\triangle DQC हा काटकोन त्रिकोण आहे. आता आपण \triangle DQC साठी पायथॅगोरसचे सूत्र वापरून बाजू CQ ची लांबी काढूया,
\begin{aligned} \\ &\therefore \ell\left(CD\right)^2=\ell\left(DQ\right)^2+\ell\left(CQ\right)^2 \\ &\therefore \ell\left(CQ\right)^2=\ell\left(CD\right)^2-\ell\left(DQ\right)^2 \\ &\therefore \ell\left(CQ\right)^2=\left(5\right)^2-\left(4\right)^2 \\ &\therefore \ell\left(CQ\right)^2=\left(25\right)-\left(16\right) \\ &\therefore \ell\left(CQ\right)^2=9 \\ &\therefore \sqrt{\ell\left(CQ\right)^2}=\sqrt{9} \\ &\therefore \mathbf{\ell\left(CQ\right)=3}\end{aligned}

पायरी 3:
तसेच \ell\left(AD\right)=\ell\left(PQ\right)=7 सेमी.
\begin{aligned} \\ &\therefore \ell\left(BC\right)=\ell\left(BP\right)+\ell\left(PQ\right)+\ell\left(QC\right) \\ &\therefore \ell\left(BC\right)=\left(3\right)+\left(7\right)+\left(3\right) \\ &\mathbf{\therefore \ell\left(BC\right)=13}\end{aligned}

पायरी 4:
समलंब चौकोनाचं क्षेत्रफळ =\frac{1}{2}\times (समांतर बाजूंच्या लांबींची बेरीज) \times उंची
\begin{aligned} \\ &\therefore A=\frac{1}{2}\times \left[\ell\left(AD\right)+\ell\left(BC\right)\right]\times \ell\left(AP\right) \\ &\therefore A=\frac{1}{2}\times \left(13+7\right)\times 4 \\ &\therefore A=\frac{1}{2}\times \left(20\right)\times 4 \\ &\therefore A=\frac{1}{2}\times 80 \\ &\mathbf{\therefore A=40}\end{aligned}
\therefore समलंब चौकोनाचे क्षेत्रफळ 40 चौरस सेमी आहे.

Go to top

त्रिकोणचे क्षेत्रफळ सूत्र

इयत्ता 8 वी साठी क्षेत्रफळ म्हणजे काय? हे समजून घेण्यासाठी आपण त्रिकोणाच्या क्षेत्रफळ सूत्राचा अभ्यास करूया,

A=\frac{1}{2}\times (पाया) \times (उंची) हे त्रिकोणाच्या क्षेत्रफळाचा सूत्र आपल्याला माहित आहे. पण जर त्रिकोणाची उंची दिलेली नसेल आणि तीन बाजूंची लांबी दिलेली असेल, तर त्रिकोणाचं क्षेत्रफळ कसं काढायचं, ते आता आपण शिकणार आहोत.

\triangle ABC मध्ये \ell\left(AB\right)=a, \ell\left(BC\right)=b आणि \ell\left(CA\right)=c
त्रिकोणाची परिमिती = (त्रिकोणाच्या तीन बाजूंच्या लांबीची बेरीज)
त्रिकोणाची अर्ध परिमिती s=\frac{1}{2}\times (त्रिकोणाच्या तीन बाजूंच्या लांबीची बेरीज)
\begin{aligned} \\ &\therefore s=\frac{1}{2}\times \left[\ell\left(AB\right)+\ell\left(BC\right)+\ell\left(CA\right)\right] \\ &\therefore s=\frac{1}{2}\times \left[a+b+c\right]\end{aligned}
त्रिकोणाची अर्ध परिमिती माहित असताना त्रिकोणाच्या क्षेत्रफळाचे सूत्र खालील प्रमाणे लिहिता येते. ह्या सूत्राला हेरनचे सूत्र (Heron’s Formula) असं म्हणतात.
हेरनच्या सूत्राने त्रिकोणाचे क्षेत्रफळ \mathbf{A=\sqrt{s\left(s-a\right)\left(s-b\right)\left(s-c\right)}}

इयत्ता 8 वी साठी क्षेत्रफळ म्हणजे काय? हे समजून घेण्यासाठी आपण त्रिकोणाच्या क्षेत्रफळाची काही उदाहरणे सोडवुया,

उदा 1:
एका त्रिकोणाच्या तीन बाजूंची लांबी अनुक्रमे 17 सेमी, 25 सेमी व 26 सेमी आहे; तर त्या त्रिकोणाचे क्षेत्रफळ काढा.

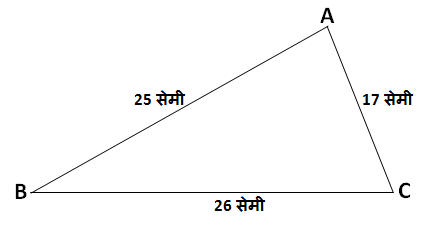
उत्तर:
इथे लक्षात घ्या की आपल्याला त्रिकोणाची उंची दिलेली नाहीये आणि त्यामुळे ह्या त्रिकोणाचे क्षेत्रफळ काढण्यासाठी आपल्याला हेरनचं सूत्र वापरावं लागणार आहे.
त्रिकोणाची परिमिती = (त्रिकोणाच्या तीन बाजूंच्या लांबीची बेरीज)
त्रिकोणाची अर्ध परिमिती s=\frac{1}{2}\times (त्रिकोणाच्या तीन बाजूंच्या लांबीची बेरीज)
\begin{aligned} \\ &s=\frac{1}{2}\times \left(17+25+26\right) \\ &s=\frac{1}{2}\times \left(68\right) \\ &s=34\end{aligned}
हेरनच्या सूत्राने त्रिकोणाचे क्षेत्रफळ A=\sqrt{s\left(s-a\right)\left(s-b\right)\left(s-c\right)}
\begin{aligned} \\ &\therefore A=\sqrt{s\left(s-a\right)\left(s-b\right)\left(s-c\right)} \\ &\therefore A=\sqrt{34\left(34-17\right)\left(34-25\right)\left(34-26\right)} \\ &\therefore A=\sqrt{34\left(17\right)\left(9\right)\left(8\right)} \\ &\therefore A=\sqrt{17\times 2\times 17\times 3\times 3\times 2\times 2\times 2} \\ &\therefore A=\sqrt{17^2\times 3^2\time 3^2\times 2^2} \\ &\therefore A=17\times 2\times 3\times 2 \\ &\therefore A=204\end{aligned}
\therefore त्रिकोणाचं क्षेत्रफळ 204 चौरस सेमी आहे.

उदा 2:
एका भूखंडाची आकृती व मापे दि ली आहेत.
\ell\left(AB\right)=60 मीटर
\ell\left(BC\right)=60 मीटर
\ell\left(AC\right)=96 मीटर
\ell\left(DP\right)=70 मीटर

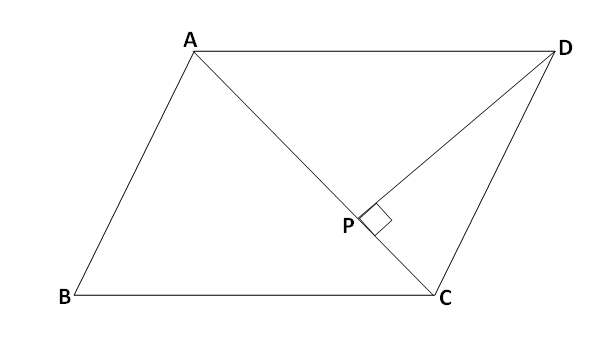
उत्तर:
दिलेली आकृती आणि दिलेलं उदाहरण लक्षपूर्वक वाचा. दिलेल्या आकृतीत \square ABCD दिलेला आहे. \square ABCD मध्ये \triangle ABC आणि \triangle ADC हे दोन त्रिकोण समाविष्ट आहेत.

\triangle ABC च्या तीन बाजूंची मापं दिलेली आहेत, पण उंची दिलेली नाही; त्यामुळे \triangle ABC चं क्षेत्रफ़ळ काढण्यासाठी आपल्याला हेरनचं सूत्र वापरावं लागणार आहे.
A=\sqrt{s\times \left(s-a\right)\left(s-b\right)\left(s-c\right)}

\triangle ADC च्या पायाचं आणि उंचीचं माप दिलेलं असल्याने आपण \triangle ADC चं क्षेत्रफळ A=\frac{1}{2}\time (पाया) \times (उंची) हे सूत्र वापरून काढावं लागणार आहे.

\triangle ABC आणि \triangle ADC च्या क्षेत्रफळांची बेरीज ही \square ABCD चं क्षेत्रफळ असेल.

पायरी 1:
\triangle ABC ची अर्ध-परिमिती:
\begin{aligned} \\ &\therefore s=\frac{1}{2}\times \left[\ell\left(AB\right)+\ell\left(BC\right)+\ell\left(CD\right)\right] \\ &\therefore s=\frac{1}{2}\times \left[\ell\left(60\right)+\ell\left(60\right)+\ell\left(96\right)\right] \\ &\therefore s=\frac{1}{2}\times 216 \\ &\mathbf{\therefore s=108}\end{aligned}

\triangle ABC चं क्षेत्रफ़ळ:
\begin{aligned} \\ &\therefore A=\sqrt{s\times \left(s-a\right)\times \left(s-b\right)\times \left(s-c\right)} \\ &\therefore A=\sqrt{108\times \left(108-60\right)\times \left(108-60\right)\times \left(108-96\right)} \\ &\therefore A=\sqrt{108\times \left(48\right)\times \left(48\right)\times \left(12\right)} \\ &\therefore A=\sqrt{12\times 3\times 3\times 12\times 4\times 12\times 4 \times 12} \\ &\therefore A=\sqrt{12^2\times 3^2\times 12^2\times 4^2} \\ &\therefore A=12\times 3\times 12\times 4 \\ &\mathbf{\therefore A=1728}\end{aligned}

पायरी 2:
\triangle ADC चं क्षेत्रफ़ळ:
\begin{aligned} \\ &\therefore A=\frac{1}{2}\times \ell\left(AC\right)\times \ell\left(DP\right) \\ &\therefore A=\frac{1}{2}\times \ell\left(96\right)\times \ell\left(70\right) \\ &\therefore A=\frac{1}{2}\times \ell\left(6720\right) \\ &\therefore A=3360\end{aligned}

पायरी 3:
भूखंड \square ABCD चं क्षेत्रफळ = (\triangle ABC चं क्षेत्रफ़ळ) + (\triangle ADC चं क्षेत्रफ़ळ)
\begin{aligned} \\ &\therefore A\left(\square ABCD\right)=A\left(\triangle ABC\right)+A\left(\triangle ADC\right) \\ &\therefore A\left(\square ABCD\right)=1728+3360 \\ &\mathbf{\therefore A\left(\square ABCD\right)=5088}\end{aligned}
\therefore भूखंडचं क्षेत्रफळ 5088 चौरस मीटर आहे.

उदा 3:
एका त्रिकोणाच्या तीन बाजूंची लांबी अनुक्रमे 45 सेमी, 39 सेमी व 42 सेमी आहे; तर त्या त्रिकोणाचे क्षेत्रफळ काढा.
उत्तर:
इथे लक्षात घ्या की आपल्याला त्रिकोणाची उंची दिलेली नाहीये आणि त्यामुळे ह्या त्रिकोणाचे क्षेत्रफळ काढण्यासाठी आपल्याला हेरनचं सूत्र वापरावं लागणार आहे.
त्रिकोणाची परिमिती = (त्रिकोणाच्या तीन बाजूंच्या लांबीची बेरीज)
त्रिकोणाची अर्ध परिमिती s=\frac{1}{2}\times (त्रिकोणाच्या तीन बाजूंच्या लांबीची बेरीज)

\begin{aligned} \\ &\therefore s=\frac{1}{2}\times \left(45+39+42\right) \\ &\therefore s=\frac{1}{2}\times \left(126\right) \\ &\therefore s=63\end{aligned}

हेरनच्या सूत्राने त्रिकोणाचे क्षेत्रफळ A=\sqrt{s\left(s-a\right)\left(s-b\right)\left(s-c\right)}
\begin{aligned} \\ &\therefore A=\sqrt{s\left(s-a\right)\left(s-b\right)\left(s-c\right)} \\ &\therefore A=\sqrt{63\times \left(63-45\right)\times \left(63-39\right)\times \left(63-42\right)} \\ &\therefore A=\sqrt{63\times \left(18\right)\times \left(24\right)\times \left(21\right)} \\ &\therefore A=\sqrt{7\times 3\times 3\times 3\times 3\times 2\times 3\times 2\times 2\times 2\times 7\times 3} \\ &\therefore A=\sqrt{7^2\times 3^2\times 3^2\times 3^2\times 2^2\times 2^2} \\ &\therefore A=7\times 3\times 3\times 3\times 2\times 2 \\ &\mathbf{\therefore A=756}\end{aligned}
\therefore त्रिकोणाचं क्षेत्रफळ 756 चौरस सेमी आहे.

उदा 4:
दिलेल्या आकृतीतील \square ABCD चं क्षेत्रफळ काढा.
\ell\left(AB\right)=36 मी, \ell\left(BC\right)=15 मी, \ell\left(CD\right)=25 मी, \ell\left(AD\right)=56 मी

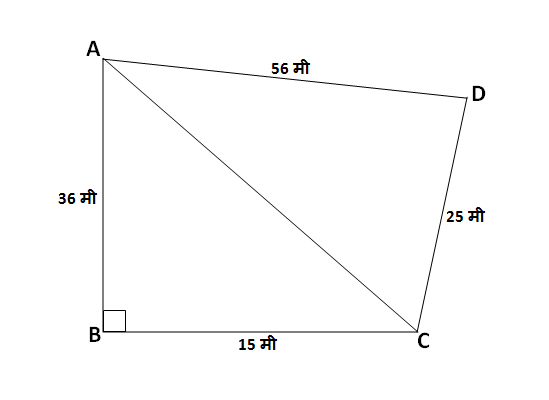
उत्तर:
दिलेल्या \square ABCD मध्ये \triangle ABC आणि \triangle ADC हे दोन त्रिकोण समाविष्ट आहेत.

\triangle ABC हा काटकोन त्रिकोण आहे. ह्या त्रिकोणाचं क्षेत्रफळ आपण A=\frac{1}{2}\times (त्रिकोणाच्या काटकोन करणाऱ्या बाजूंच्या लांबींचा गुणाकार), हे सूत्र वापरून काढू शकतो.

\triangle ADC च्या बाजू AD आणि बाजू CD ची लांबी आपल्याला माहित आहे. ह्या त्रिकोणाची उंची दिलेली नाही; त्यामुळे \triangle ADC चं क्षेत्रफळ काढण्यासाठी आपल्याला हेरनचं सूत्र वापरावं लागणार आहे. पण हेरनचं सूत्र वापरण्यासाठी आपल्याला बाजू AC ची लांबी माहित असणे आवश्यक आहे.

आपण आधीच माहित आहे की \triangle ABC हा काटकोन त्रिकोण आहेआणि त्यामुळे \triangle ABC साठी पायथॅगोरसचं सूत्र वापरून आपण बाजू AC ची लांबी काढू शकतो.

पायरी 1:
\triangle ABC चं क्षेत्रफ़ळ:
\begin{aligned} \\ &\therefore A=\frac{1}{2}\times \ell\left(AB\right)\times +\ell\left(BC\right) \\ &\therefore A=\frac{1}{2}\times \left(36\right)\times +\left(15\right) \\ &\therefore A=\frac{1}{2}\times \left(540\right) \\ &\mathbf{\therefore \ell\left(AC\right)=270}\end{aligned}
\mathbf{\triangle ABC} चं क्षेत्रफ़ळ 270 चौरस मीटर आहे.

पायरी 2:
पायथॅगोरसचं सूत्र वापरून आपण बाजू AC ची लांबी काढू,
\begin{aligned} \\ &\therefore \ell\left(AC\right)^2=\ell\left(AB\right)^2+\ell\left(BC\right)^2 \\ &\therefore \ell\left(AC\right)^2=\left(36\right)^2+\left(15\right)^2 \\ &\therefore \ell\left(AC\right)^2=\left(1296\right)+\left(225\right) \\ &\therefore \ell\left(AC\right)^2=1521 \\ &\therefore \ell\left(AC\right)=\sqrt{1521} \\ &\therefore \ell\left(AC\right)=39\end{aligned}

इथे लक्षात घ्या की आपल्याला त्रिकोणाची उंची दिलेली नाहीये आणि त्यामुळे ह्या त्रिकोणाचे क्षेत्रफळ काढण्यासाठी आपल्याला हेरनचं सूत्र वापरावं लागणार आहे.
त्रिकोणाची परिमिती = (त्रिकोणाच्या तीन बाजूंच्या लांबीची बेरीज)
त्रिकोणाची अर्ध परिमिती s=\frac{1}{2}\times (त्रिकोणाच्या तीन बाजूंच्या लांबीची बेरीज)
\begin{aligned} \\ &\therefore s=\frac{1}{2}\times \left(56+25+39\right) \\ &\therefore s=\frac{1}{2}\times \left(120\right) \\ &\therefore s=60\end{aligned}

हेरनच्या सूत्राने त्रिकोणाचे क्षेत्रफळ A=\sqrt{s\left(s-a\right)\left(s-b\right)\left(s-c\right)}
\begin{aligned} \\ &\therefore A=\sqrt{s\left(s-a\right)\left(s-b\right)\left(s-c\right)} \\ &\therefore A=\sqrt{60\times \left(60-56\right)\times \left(60-25\right)\times \left(60-39\right)} \\ &\therefore A=\sqrt{60\times \left(4\right)\times \left(35\right)\times \left(21\right)} \\ &\therefore A=\sqrt{4\times 3\times 5\times 4\times 7\times 5\times 7\times 3} \\ &\therefore A=\sqrt{7^2\times 5^2\times 4^2\times 3^2} \\ &\therefore A=7\times 5\times 4\times 3 \\ &\mathbf{\therefore A=420}\end{aligned}
\mathbf{\triangle ABC} चं क्षेत्रफ़ळ 420 चौरस मीटर आहे.

पायरी 3:
\square ABCD चं क्षेत्रफळ = (\triangle ABC चं क्षेत्रफ़ळ) + (\triangle ADC चं क्षेत्रफ़ळ)
\begin{aligned} \\ &\therefore A\left(\square ABCD\right)=A\left(\triangle ABC\right)+A\left(\triangle ADC\right) \\ &\therefore A\left(\square ABCD\right)=270+420 \\ &\mathbf{\therefore A\left(\square ABCD\right)=690}\end{aligned}
\therefore \square ABCD चं क्षेत्रफळ 690 चौरस मीटर आहे.

उदा 5:
खाली दिलेल्या मापांवरून शेजारील आकृतीत दिलेल्या \square ABCD चं क्षेत्रफळ काढा.
\ell\left(AB\right)=40 मीटर
\ell\left(BC\right)=9 मीटर
\ell\left(CD\right)=60 मीटर
\ell\left(AP\right)=13 मीटर

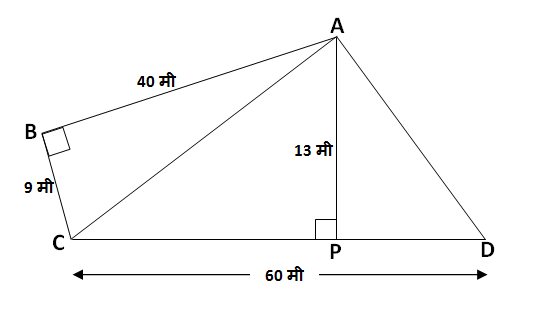
उत्तर:
\square ABCD मध्ये \triangle ABC आणि \triangle ACD समाविष्ट आहेत.\

पायरी 1:
\triangle ABC हा काटकोन त्रिकोण आहे.
काटकोन त्रिकोणाचं क्षेत्रफळ =\frac{1}{2}\times (काटकोन करणाऱ्या बाजूंच्या लांबीचा गुणाकार)
\begin{aligned} \\ &\therefore A\left(\triangle ABC\right)=\frac{1}{2}\times \ell\left(AB\right)\times \ell\left(BC\right) \\ &\therefore A\left(\triangle ABC\right)=\frac{1}{2}\times \left(40\right)\times \left(9\right) \\ &\therefore A\left(\triangle ABC\right)=\frac{1}{2}\times \left(360\right) \\ &\mathbf{\therefore A\left(\triangle ABC\right)=180}\end{aligned}
\mathbf{\therefore \triangle ABC} चं क्षेत्रफळ 180 चौरस मीटर आहे.

पायरी 2:
\triangle ACD चं क्षेत्रफळ =\frac{1}{2}\times (पाया) \times (उंची)
\begin{aligned} \\ &\therefore A\left(\triangle ACD\right)=\frac{1}{2}\times \ell\left(CD\right)\times \ell\left(AP\right) \\ &\therefore A\left(\triangle ACD\right)=\frac{1}{2}\times \left(60\right)\times \left(13\right) \\ &\therefore A\left(\triangle ACD\right)=\frac{1}{2}\times \left(780\right) \\ &\mathbf{\therefore A\left(\triangle ABC\right)=390}\end{aligned}

\mathbf{\therefore \triangle ACD} चं क्षेत्रफळ 390 चौरस मीटर आहे.

पायरी 3:
\square ABCD चं क्षेत्रफळ = (\triangle ABC चं क्षेत्रफळ) + (\triangle ACD चं क्षेत्रफळ )
\begin{aligned} \\ &\therefore A\left(\square ABCD\right)=A\left(\triangle ABC\right)+A\left(\triangle ACD\right) \\ &\therefore A\left(\square ABCD\right)=\left(180\right)+\left(390\right) \\ &\mathbf{\therefore A\left(\square ABCD\right)=\left(570\right)}\end{aligned}
\mathbf{\therefore \square ABCD} चं क्षेत्रफळ 570 चौरस मीटर आहे.

Go to top

वर्तुळाचे क्षेत्रफळ सूत्र

इयत्ता 8 वी साठी क्षेत्रफळ म्हणजे काय? हे समजून घेण्यासाठी आपण वर्तुळाच्या क्षेत्रफळ सूत्राचा अभ्यास करूया,

वर्तुळाविषयी काही प्राथमिक गोष्टींची माहिती करून घेऊया,

वर्तुळाचं केंद्र: बिंदू C ला वर्तुळाचं केंद्र म्हणतात.

परीघ: वर्तुळाच्या सीमेवरून, म्हणजे बिंदू A पासून बिंदू P पर्यंत -> बिंदू P पासून बिंदू B पर्यंत -> बिंदू B पासून बिंदू Q पर्यंत -> बिंदू Q पासून बिंदू A पर्यंत, अशी एक पूर्ण गोल फेरी जर आपण मारली, तर त्या पूर्ण गोल मार्गाला वर्तुळाचा परीघ म्हणतात.

वर्तुळाची त्रिज्या: वर्तुळाच्या केंद्रापासून परिघापर्यंतच्या अंतराला वर्तुळाची त्रिज्या म्हणतात. वर्तुळाची त्रिज्या r (आर) ह्या इंग्रजी अक्षराने दर्शवतात. वरील आकृतीत वर्तुळाची त्रिज्या r=\ell\left(AC\right)=\ell\left(BC\right)=\ell\left(PC\right)=\ell\left(QC\right)

वर्तुळाचा व्यास: वर्तुळाची दोन सामान अर्धवर्तुळात विभागणी करणाऱ्या रेषाखंडला वर्तुळाचा व्यास म्हणतात. व्यास हा वर्तुळाच्या केंद्र बिंदूतून जातो आणि परिघावरील समोरासमोरच्या दोन बिंदूंना छेदतो. म्हणजेच व्यास हा त्रिज्येच्या दुप्पट लांबीचा असतो. वरील आकृतीत रेख AB आणि रेख PQ हे वर्तुळाचे व्यास आहेत.
वर्तुळाचा व्यास D=2\times r

इयत्ता 8 वी साठी क्षेत्रफळ म्हणजे काय? हे समजून घेण्यासाठी आपण वर्तुळाच्या क्षेत्रफळाची काही उदाहरणे सोडवुया,

उदा 1:
एका वर्तुळाची त्रिज्या 21 सेमी असेल तर त्या वर्तुळाचे क्षेत्रफळ काढा.
उत्तर:
वर्तुळाची त्रिज्या r=21 सेमी
वर्तुळाचं क्षेत्रफळ A=\pi\times r^2
\begin{aligned} \\ &\therefore A=\pi\times r^2 \\ &\therefore A=\frac{22}{7}\times 21^2 \\ &\therefore A=\frac{22}{7}\times 441 \\ &\therefore A=22\times 63 \\ &\mathbf{\therefore A=1386}\end{aligned}
म्हणून वर्तुळाचं क्षेत्रफळ 1386 चौरस सेमी आहे.

उदा 2:
एका वर्तुळाकृती मैदानाचे क्षेत्रफळ 3850 चौमी आहे, तर त्या मैदानाची त्रिज्या काढा.
उत्तर:
वर्तुळाचं क्षेत्रफळ A=3850 चौमी
वर्तुळाचं क्षेत्रफळ सूत्र A=\pi\times r^2
\begin{aligned} \\ &\therefore A=\pi\times r^2 \\ &\therefore 3850=\frac{22}{7}\times r^2 \\ &\therefore r^2=\frac{3850\times 7}{22} \\ &\therefore r^2=\frac{26950}{22} \\ &\therefore r^2=1225 \\ &\therefore \sqrt{r^2}=\sqrt{1225} \\ &\mathbf{\therefore r=35}\end{aligned}
म्हणून वर्तुळाची त्रिज्या 35 मीटर आहे.

उदा 3:
खाली वर्तुळांच्या त्रिज्या दिल्या आहेत. त्या वर्तुळांची क्षेत्रफळे काढा.
उत्तर:

उदा 4:
खाली काही वर्तुळांची क्षेत्रफळे दिली आहेत. त्या वर्तुळांचे व्यास काढा.
उत्तर:

उदा 5:
एका वर्तुळाकार बागेचा व्यास 42 मीटर आहे. त्या बागेभोवती 3.5 मीटर रुंदीचा रस्ता आहे, तर त्या रस्त्याचे क्षेत्र फळ काढा.

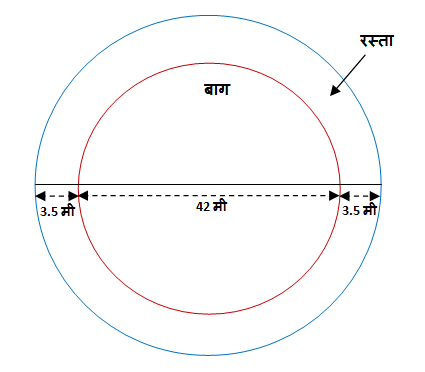
उत्तर:
आता रस्त्याचं क्षेत्रफळ काढण्यासाठी आपल्याला बाहेरच्या वर्तुळाच्या क्षेत्रफळातून आतल्या बागेच्या वर्तुळाचं क्षेत्रफळ वजा करावं लागणार आहे.

पायरी 1:
आपल्याला बागेच्या वर्तुळाचा व्यासाची लांबी 42 मीटर दिलेली आहे.
त्रिज्या = व्यास / 2
r_i=\frac{42}{2}=21 मीटर.

आता आपण आधी बागेच्या वर्तुळाचं क्षेत्रफळ काढून घेऊ,
\begin{aligned} \\ &A_i=\pi\times r_i^2 \\ &\therefore A_i=\frac{22}{7}\times \left(21\right)^2 \\ &\therefore A_i=\frac{22}{7}\times 441 \\ &\therefore A_i=22\times 63 \\ &\therefore A_i=1386\end{aligned}
\therefore बागेच्या वर्तुळाचं क्षेत्रफळ 1386 चौरस मीटर आहे.

पायरी 2:
बाहेरच्या, म्हणजे रस्त्याच्या वर्तुळाचं क्षेत्रफळ काढण्याआधी आपल्याला त्या वर्तुळाचा व्यास किती लांबीचा आहे, ते निश्चित करावं लागणार आहे आणि त्यावरून त्या वर्तुळाची त्रिज्या काढावी लागणार आहे.
आता वर दिलेली आकृती लक्षपूर्वक बघा. बागेच्या वर्तुळाचा व्यास 42 मीटर आहे. बागेच्या वर्तुळाच्या बाहेरून रस्त्याचं वर्तुळ आहे आणि त्या रस्त्याची रुंदी 3.5 मीटर आहे. त्यामुळे रस्त्याच्या वर्तुळाचा व्यास काढण्यासाठी आपल्याला बागेच्या वर्तुळाच्या व्यासात रस्त्याची रुंदी मिळवावी लागणार आहे.

महत्वाचं: पण बागेच्या व्यासाच्या दोन्ही टोकांच्या बाहेर 3.5 मीटर रुंदीचा रस्ता आहे, हे लक्षात घ्या.
\mathbf{\therefore } रस्त्याच्या वर्तुळाचा व्यास \mathbf{=(} बागेच्या वर्तुळाचा व्यास\mathbf{)+2\times (} रस्त्याची रुंदी ).
\begin{aligned} \\ &\therefore D_o=42+2\times \left(3.5\right) \\ &\therefore D_o=42+7 \\ &\therefore D_o=49\end{aligned}

\therefore रस्त्याच्या वर्तुळाची त्रिज्या = व्यास / 2
\begin{aligned} \\ &\therefore r_o=\frac{D_o}{2} \\ &\therefore r_o=\frac{49}{2} \\ &\therefore r_o=24.5\end{aligned}

\therefore रस्त्याच्या वर्तुळाचं क्षेत्रफळ
\begin{aligned} \\ &A_o=\pi\times r_o^2 \\ &\therefore A_o=\frac{22}{7}\times \left(24.5\right)^2 \\ &\therefore A_o=\frac{22}{7}\times 600.25 \\ &\therefore A_o=22\times 85.75 \\ &\therefore A_o=1886.5\end{aligned}
\therefore रस्त्याच्या वर्तुळाचं क्षेत्रफळ 1886.5 चौरस मीटर आहे.

पायरी 3:
\therefore रस्त्याचं क्षेत्रफळ = (रस्त्याच्या वर्तुळाचं क्षेत्रफळ) – (बागेच्या वर्तुळाचं क्षेत्रफळ)
\begin{aligned} \\ &\therefore A=A_o-A_i \\ &\therefore A=1886.5-1386 \\ &\therefore A=500.50\end{aligned}
\mathbf{\therefore } रस्त्याचं क्षेत्रफळ 500.50 चौरस मीटर आहे.

उदा 6:
एका वर्तुळाचा परीघ 88 सेमी आहे, तर त्या वर्तुळाचे क्षेत्रफळ काढा.
उत्तर:

वर्तुळाचा परीघ P=2\times \pi\times r
\begin{aligned} \\ &\therefore P=2\times \pi\times r \\ &\therefore 88=2\times \frac{22}{7}\times r \\ &\therefore 88=\frac{44}{7}\times r \\ &\therefore 88\times 7=44\times r \\ &\therefore 616=44\times r \\ &\therefore r=\frac{616}{44} \\ &\therefore r=14\end{aligned}
\therefore वर्तुळाची त्रिज्या 14 सेमी आहे.

वर्तुळाचं क्षेत्रफळ A=\pi\times r^2
\begin{aligned} \\ &A=\pi\times r^2 \\ &\therefore A=\frac{22}{7}\times \left(14\right)^2 \\ &\therefore A=\frac{22}{7}\times 196 \\ &\therefore A=22\times 28 \\ &\therefore A=616\end{aligned}
\mathbf{\therefore } वर्तुळाचं क्षेत्रफळ 616 चौरस सेमी आहे.

Go to top

अनियमित आकाराच्या जागेचे क्षेत्रफळ

इयत्ता 8 वी साठी क्षेत्रफळ म्हणजे काय? हे समजून घेण्यासाठी आपण अनियमित आकाराच्या क्षेत्रफळ सूत्राचा अभ्यास करूया,

अनियमित आकाराचं क्षेत्रफळ काढण्यासाठी त्या आकाराला विविध नियमित आकारांमध्ये विभाजित केलं जातं आणि त्या प्रत्येक नियमित आकाराच्या क्षेत्रफळांची बेरीज, ही त्या अनियमित आकाराचं क्षेत्रफळ असतं. आपण हे उदाहरणावरून समजावून घेऊ,

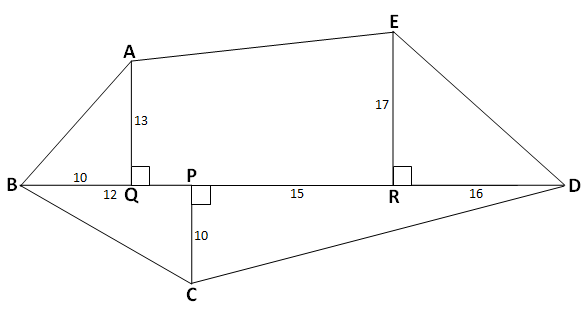
वर दिलेल्या आकृतीत ABCDE हा अनियमित आकार दिलेला आहे आणि आपल्याला त्याचं क्षेत्रफळ काढायचं आहे. ह्या अनियमित आकाराच्या आकृतीचं क्षेत्रफळ काढण्यासाठी ह्या आकाराला आपण विविधं नियमित आकारामध्ये विभाजीत करून घेतलं आहे. आता आपल्याला त्या प्रत्येक नियमित आकाराचं क्षेत्रफळ काढावं लागणार आहे.

(1) \triangle AQB हा काटकोन त्रिकोण आहे.
\begin{aligned} \\ &\therefore A\left(\triangle AQB\right)=\frac{1}{2}\times \ell\left(AQ\right)\times \ell\left(BQ\right) \\ &\therefore A\left(\triangle AQB\right)=\frac{1}{2}\times 13\times (10) \\ &\therefore A\left(\triangle AQB\right)=\frac{1}{2}\times 130 \\ &\therefore A\left(\triangle AQB\right)=65\end{aligned}
\therefore \triangle AQB चं क्षेत्रफळ आहे 65 चौरस मीटर आहे.

(2) \triangle BPC हा काटकोन त्रिकोण आहे.
\begin{aligned} \\ &\therefore A\left(\triangle BPC\right)=\frac{1}{2}\times \ell\left(BP\right)\times \ell\left(CP\right) \\ &\therefore A\left(\triangle BPC\right)=\frac{1}{2}\times 10\times \left(12+10\right) \\ &\therefore A\left(\triangle BPC\right)=\frac{1}{2}\times 220 \\ &\therefore A\left(\triangle BPC\right)=110\end{aligned}
\therefore \triangle BPC चं क्षेत्रफळ आहे 110 चौरस मीटर आहे.

(3) \triangle CPD हा काटकोन त्रिकोण आहे.
\begin{aligned} \\ &\therefore A\left(\triangle CPD\right)=\frac{1}{2}\times \ell\left(CP\right)\times \ell\left(DP\right) \\ &\therefore A\left(\triangle CPD\right)=\frac{1}{2}\times 10\times \left(15+16\right) \\ &\therefore A\left(\triangle CPD\right)=\frac{1}{2}\times 310 \\ &\therefore A\left(\triangle CPD\right)=155\end{aligned}
\therefore \triangle CPD चं क्षेत्रफळ आहे 155 चौरस मीटर आहे.

(4) \triangle ERD हा काटकोन त्रिकोण आहे.
\begin{aligned} \\ &\therefore A\left(\triangle ERD\right)=\frac{1}{2}\times \ell\left(ER\right)\times \ell\left(DR\right) \\ &\therefore A\left(\triangle ERD\right)=\frac{1}{2}\times 16\times 17 \\ &\therefore A\left(\triangle ERD\right)=\frac{1}{2}\times 272 \\ &\therefore A\left(\triangle ERD\right)=136\end{aligned}
\therefore \triangle ERD चं क्षेत्रफळ आहे 136 चौरस मीटर आहे.

(5) \square AQRE हा समलंब चौकोन आहे.
\begin{aligned} \\ &\therefore A\left(\square AQRE\right)=\frac{1}{2}\times \left[\ell\left(AQ\right)+\ell\left(ER\right)\right]\times \ell\left(QR\right) \\ &\therefore A\left(\square AQRE\right)=\frac{1}{2}\times \left[13+17\right]\times \left(12+15\right) \\ &\therefore A\left(\square AQRE\right)=\frac{1}{2}\times \left(30\right)\times \left(27\right) \\ &\therefore A\left(\square AQRE\right)=\frac{1}{2}\times \left(810\right) \\ &\therefore A\left(\square AQRE\right)=405\end{aligned}
\therefore \square AQRE चं क्षेत्रफळ आहे 405 चौरस मीटर आहे.

\therefore बहुभुजाकृती ABCDE चं क्षेत्रफळ,
\begin{aligned} \\ &\therefore A\left(ABCDE\right)=A\left(\triangle AQB\right)+A\left(\triangle BPC\right)+A\left(\triangle CPD\right)+A\left(\triangle ERD\right)+A\left(\square AQRE\right) \\ &\therefore A\left(ABCDE\right)=\left(65\right)+\left(110\right)+\left(155\right)+\left(136\right)+\left(405\right) \\ &\therefore A\left(ABCDE\right)=871\end{aligned}
\mathbf{\therefore } बहुभुजाकृती ABCDE चं क्षेत्रफळ 871 चौरस मीटर आहे.

इयत्ता 8 वी साठी क्षेत्रफळ म्हणजे काय? हे समजून घेण्यासाठी आपण बहुभुजाकृतीच्या क्षेत्रफळाची काही उदाहरणे सोडवुया,

उदा 1:
खालील बहुभुजाकृतीचं क्षेत्रफळ काढा.

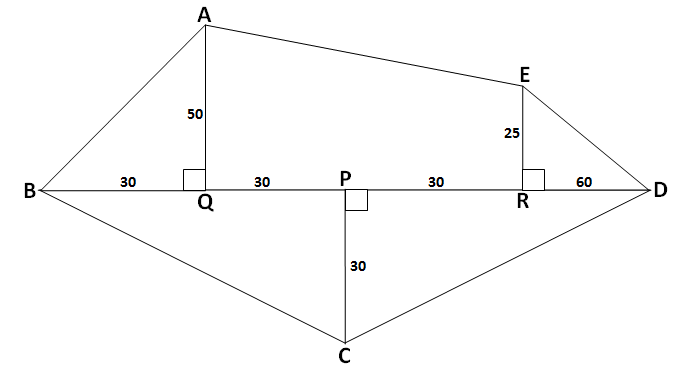
उत्तर:
दिलेली बहुभुजाकृती ABCDE हा अनियमित आकार आहे आणि आपल्याला त्याचं क्षेत्रफळ काढायचं आहे. ह्या बहुभुजाकृतीचं क्षेत्रफळ काढण्यासाठी ह्या बहुभुजाकृतीला आपण विविधं नियमित आकारामध्ये विभाजीत करून घेतलं आहे. आता आपल्याला त्या प्रत्येक नियमित आकाराचं क्षेत्रफळ काढावं लागणार आहे. आकृतीमध्ये दिलेली बाजूंची मापं मीटरमध्ये आहेत.

(1) \triangle AQB हा काटकोन त्रिकोण आहे.
\begin{aligned} \\ &\therefore A\left(\triangle AQB\right)=\frac{1}{2}\times \ell\left(AQ\right)\times \ell\left(BQ\right) \\ &\therefore A\left(\triangle AQB\right)=\frac{1}{2}\times 50\times (30) \\ &\therefore A\left(\triangle AQB\right)=\frac{1}{2}\times 1500 \\ &\therefore A\left(\triangle AQB\right)=750\end{aligned}
\therefore \triangle AQB चं क्षेत्रफळ आहे 750 चौरस मीटर आहे.

(2) \triangle BPC हा काटकोन त्रिकोण आहे.
\begin{aligned} \\ &\therefore A\left(\triangle BPC\right)=\frac{1}{2}\times \ell\left(BP\right)\times \ell\left(CP\right) \\ &\therefore A\left(\triangle BPC\right)=\frac{1}{2}\times 30\times \left(30+30\right) \\ &\therefore A\left(\triangle BPC\right)=\frac{1}{2}\times 1800 \\ &\therefore A\left(\triangle BPC\right)=900\end{aligned}
\therefore \triangle BPC चं क्षेत्रफळ आहे 900 चौरस मीटर आहे.

(3) \triangle CPD हा काटकोन त्रिकोण आहे.
\begin{aligned} \\ &\therefore A\left(\triangle CPD\right)=\frac{1}{2}\times \ell\left(CP\right)\times \ell\left(DP\right) \\ &\therefore A\left(\triangle CPD\right)=\frac{1}{2}\times 30\times \left(30+60\right) \\ &\therefore A\left(\triangle CPD\right)=\frac{1}{2}\times 2700 \\ &\therefore A\left(\triangle CPD\right)=1350\end{aligned}
\therefore \triangle CPD चं क्षेत्रफळ आहे 1350 चौरस मीटर आहे.

(4) \triangle ERD हा काटकोन त्रिकोण आहे.
\begin{aligned} \\ &\therefore A\left(\triangle ERD\right)=\frac{1}{2}\times \ell\left(ER\right)\times \ell\left(DR\right) \\ &\therefore A\left(\triangle ERD\right)=\frac{1}{2}\times 25\times 60 \\ &\therefore A\left(\triangle ERD\right)=\frac{1}{2}\times 1500 \\ &\therefore A\left(\triangle ERD\right)=750\end{aligned}
\therefore \triangle ERD चं क्षेत्रफळ आहे 750 चौरस मीटर आहे.

(5) \square AQRE हा समलंब चौकोन आहे.
\begin{aligned} \\ &\therefore A\left(\square AQRE\right)=\frac{1}{2}\times \left[\ell\left(AQ\right)+\ell\left(ER\right)\right]\times \ell\left(QR\right) \\ &\therefore A\left(\square AQRE\right)=\frac{1}{2}\times \left[25+50\right]\times \left(30+30\right) \\ &\therefore A\left(\square AQRE\right)=\frac{1}{2}\times \left(75\right)\times \left(60\right) \\ &\therefore A\left(\square AQRE\right)=\frac{1}{2}\times \left(4500\right) \\ &\therefore A\left(\square AQRE\right)=2250\end{aligned}
\therefore \square AQRE चं क्षेत्रफळ आहे 2250 चौरस मीटर आहे.

\therefore बहुभुजाकृती ABCDE चं क्षेत्रफळ,
\begin{aligned} \\ &\therefore A\left(ABCDE\right)=A\left(\triangle AQB\right)+A\left(\triangle BPC\right)+A\left(\triangle CPD\right)+A\left(\triangle ERD\right)+A\left(\square AQRE\right) \\ &\therefore A\left(ABCDE\right)=\left(750\right)+\left(900\right)+\left(1350\right)+\left(750\right)+\left(2250\right) \\ &\therefore A\left(ABCDE\right)=6000\end{aligned}
\mathbf{\therefore } बहुभुजाकृती ABCDE चं क्षेत्रफळ 6000 चौरस मीटर आहे.

उदा 2:
खालील बहुभुजाकृतीचं क्षेत्रफळ काढा.

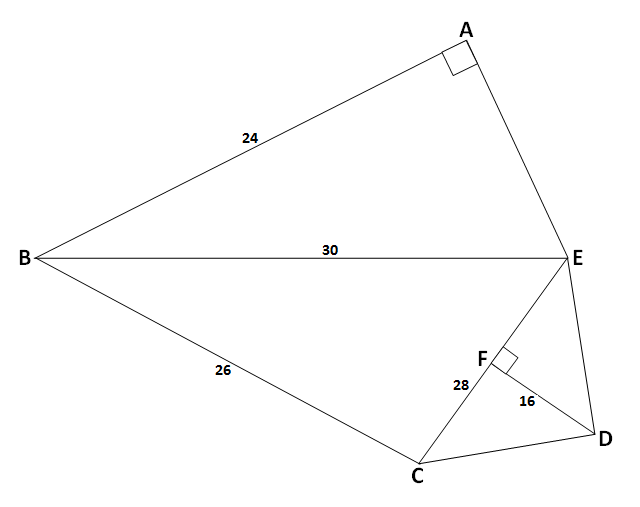
वर आकृतीत आपल्याला बहुभुजाकृती ABCDE चं क्षेत्रफळ काढायचं आहे. त्यासाठी आपण बहुभुजाकृती ABCDE ला विविध नियमित आकारांनी विभाजित करून घेतलेलं आहे. त्यामुळे आपल्याला \triangle ABE, \triangle CBE आणि \triangle CDE ह्या तीन त्रिकोणांचं क्षेत्रफळ काढून त्यांची बेरीज करावी लागणार आहे.

(1) \triangle ABE हा काटकोन त्रिकोण आहे आणि ह्या त्रिकोणाचं क्षेत्रफळ काढण्यासाठी त्याच्या बाजू AE ची लांबी आपल्याला आधी काढून घ्यावी लागणार आहे आणि त्यासाठी आपल्याला पायथॅगोरसचं सूत्र वापरावं लागणार आहे.

\begin{aligned} \\ &\therefore \ell\left(BE\right)^2=\ell\left(AB\right)^2+\ell\left(AE\right)^2 \\ &\therefore \left(30\right)^2=\left(24\right)^2+\ell\left(AE\right)^2 \\ &\therefore \left(900\right)=\left(576\right)+\ell\left(AE\right)^2 \\ &\therefore \left(AE\right)^2=\left(900\right)-\left(576\right) \\ &\therefore \ell\left(AE\right)^2=324 \\ &\therefore \sqrt{\ell\left(AE\right)^2}=\sqrt{324} \\ &\therefore \ell\left(AE\right)=18 \\\end{aligned}

\triangle ABE चं क्षेत्रफळ =\frac{1}{2}\times (काटकोन करणाऱ्या बाजूंच्या लांबीचा गुणाकार).

\begin{aligned} \\ &\therefore A\left(\triangle ABE\right)=\frac{1}{2}\times \ell\left(AB\right)\times \ell\left(AE\right) \\ &\therefore A\left(\triangle ABE\right)=\frac{1}{2}\times \left(24\right)\times \left(18\right) \\ &\therefore A\left(\triangle ABE\right)=\frac{1}{2}\times \left(432\right) \\ &\therefore A\left(\triangle ABE\right)=216\end{aligned}
\mathbf{\therefore \triangle ABE} चं क्षेत्रफळ 216 चौरस मीटर आहे.

(2) \triangle CBE चं क्षेत्रफळ: इथे एक लक्षात घ्या की आपल्याला \triangle CBE च्या तीनही बाजूंची लांबी माहित आहे, पण आपल्याला \triangle CBE ची उंची माहित नाही. त्यामुळे \triangle CBE चं क्षेत्रफळ काढण्यासाठी आपल्याला “हेरनचं सूत्र” वापरावं लागणार आहे.

\triangle CBE चं क्षेत्रफळ =\sqrt{s\left(s-a\right)\left(s-b\right)\left(s-c\right)}

इथे s=\triangle CBE ची अर्धपरिमिती,

\therefore s=\triangle CBE=\frac{1}{2}\times (त्रिकोणाच्या तीन बाजूंच्या लांबीची बेरीज)
\begin{aligned} \\ &\therefore s=\frac{1}{2}\times \left[\ell\left(BE\right)+\ell\left(BC\right)+\ell\left(CE\right)\right] \\ &\therefore s=\frac{1}{2}\times \left[\ell\left(30\right)+\ell\left(26\right)+\ell\left(28\right)\right] \\ &\therefore s=\frac{1}{2}\times \left(84\right) \\ &\therefore s=42\end{aligned}

\begin{aligned} \\ &A\left(\triangle CBE\right)=\sqrt{s\times \left(s-a\right)\times \left(s-b\right)\times \left(s-c\right)} \\ &A\left(\triangle CBE\right)=\sqrt{42\times \left(42-30\right)\times \left(42-26\right)\times \left(42-28\right)} \\ &A\left(\triangle CBE\right)=\sqrt{42\times \left(12\right)\times \left(16\right)\times \left(14\right)} \\ &A\left(\triangle CBE\right)=\sqrt{112896} \\ &A\left(\triangle CBE\right)=336\end{aligned}

\mathbf{\therefore \triangle CBE} चं क्षेत्रफळ 336 चौरस मीटर आहे.

(3) \triangle CDE चं क्षेत्रफळ =\frac{1}{2}\times (पाया) \times (उंची)

\begin{aligned} \\ &\therefore A\left(\triangle CDE\right)=\frac{1}{2}\times \ell\left(CE\right)\times \ell\left(FD\right) \\ &\therefore A\left(\triangle CDE\right)=\frac{1}{2}\times \left(28\right)\times \left(16\right) \\ &\therefore A\left(\triangle CDE\right)=\frac{1}{2}\times \left(448\right) \\ &\therefore A\left(\triangle CDE\right)=224\end{aligned}
\mathbf{\therefore \triangle CDE} चं क्षेत्रफळ 224 चौरस मीटर आहे.

\therefore बहुभुजाकृती ABCDE चं क्षेत्रफळ =A\left(\triangle ABE\right)+A\left(\triangle CBE\right)+A\left(\triangle CDE\right)

\begin{aligned} \\ &\therefore A\left(ABCDE\right)=A\left(\triangle ABE\right)+A\left(\triangle CBE\right)+A\left(\triangle CDE\right) \\ &\therefore A\left(ABCDE\right)=\left(216\right)+\left(336\right)+\left(224\right) \\ &\therefore A\left(ABCDE\right)=776\end{aligned}
\mathbf{\therefore } बहुभुजाकृती ABCDE चं क्षेत्रफळ 776 चौरस मीटर आहे.

Go to top

अनियमित आकाराच्या आकृतीचे अंदाजे क्षेत्रफळ काढणे

इयत्ता 8 वी साठी क्षेत्रफळ म्हणजे काय? हे समजून घेण्यासाठी आपण अनियमित आकाराचे क्षेत्रफळ कसे काढले जाते, ते बघूया,

एखाद्या अनियमित आकाराच्या आकृतीचं अंदाजे क्षेत्रफळ काढण्यासाठी आपल्याला आलेख कागदाचा वापर करावा लागतो. त्यासाठी ती अनियमित आकाराची आकृती आलेख कागदावर काढून घ्यावी लागते आणि त्या अनियमित आकारात समाविष्ट झालेले आलेख कागदावरील ठराविक क्षेत्रफळाचे चौरस मोजून आपण ह्या अनियमित आकाराच्या आकृतीचं अंदाजे क्षेत्रफळ काढू शकतो. जेवढं आलेख कागदावरील चौरसांचं क्षेत्रफळ कमी, तेवढं त्या अनियमित आकाराचं क्षेत्रफळ अधिक बरोबर असतं.
आपण आता एका उदाहरणावरून ही संकल्पना समजावून घेऊ,

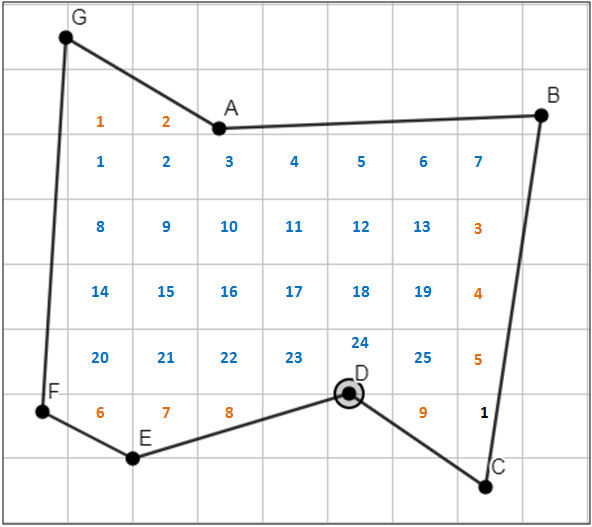
वर दिलेल्या आकृतीत आलेख कागदावर बहुभुजाकृती ABCDEFG काढलेली आहे. ह्या आकृतीने आलेख कागदावरचे व्यापलेले चौरस वापरून आपण ह्या बहुभुजाकृतीचं अंदाजे क्षेत्रफळ खालील प्रमाणे काढू शकतो,

(1) बहुभुजाकृती ABCDEFG ने व्यापलेल्या आलेख कागदावरील 1 चौरस सेमी क्षेत्रफळ असणाऱ्या पूर्ण चौरसांची संख्या विचारात घेऊ. आकृतीत दिलेले निळ्या रंगाच्या आकड्यांनी दर्शविलेले सर्व चौरस हे 1 चौरस सेमी क्षेत्रफळाचे आहेत आणि त्यांची संख्या 25 आहे.
म्हणून ह्या 1 चौरस सेमी क्षेत्रफळ असणाऱ्या सर्व चौरसांचं एकत्रित क्षेत्रफळ =25 चौरस सेमी.

(2) आकृतीतील अर्ध्या चौरस सेमी पेक्षा जास्त परंतु 1 चौरस सेमी पेक्षा कमी क्षेत्रफळ असणारे भाग विचारात घेऊ. आकृतिमध्ये नारिंगी रंगाच्या आकड्यांनी दर्शविलेले भाग हे अर्ध्या चौरस सेमी पेक्षा जास्त परंतु 1 चौरस सेमी पेक्षा कमी क्षेत्रफळ असणारे भाग आहेत आणि त्यांची संख्या 9 आहे.
म्हणून ह्या अर्ध्या चौरस सेमी पेक्षा जास्त परंतु 1 चौरस सेमी पेक्षा कमी क्षेत्रफळ असणाऱ्या भागांचं क्षेत्रफळ =9 चौरस सेमी.

(3) आता आकृतीतील अर्धा चौरस सेमी क्षेत्रफळ असणारे भाग विचारात घेऊ. आकृतिमध्ये काळ्या रंगाच्या आकड्यांनी दर्शविलेले भाग हे अर्धा चौरस सेमी क्षेत्रफळ असणारे भाग आहेत आणि त्यांची संख्या फक्त 1 आहे.
म्हणून ह्या अर्धा चौरस सेमी क्षेत्रफळ असणाऱ्या भागांचं क्षेत्रफळ =\frac{1}{2}=0.5 चौरस सेमी.

(4) आकृतीतील अर्ध्या सेमीपेक्षा कमी क्षेत्रफळ असलेल्या भागांचा विचार करायचा नाही आणि त्यामुळे अशा भागांचं क्षेत्रफळ =0 चैरस सेमी.

म्हणून दिलेल्या बहुभुजाकृतीचं अंदाजे क्षेत्रफळ = (1 चौरस सेमी क्षेत्रफळ असणाऱ्या सर्व चौरसांचं क्षेत्रफळ) + (अर्ध्या चौरस सेमी पेक्षा जास्त परंतु 1 चौरस सेमी पेक्षा कमी क्षेत्रफळ असणाऱ्या भागांचं क्षेत्रफळ) + (अर्धा चौरस सेमी क्षेत्रफळ असणाऱ्या भागांचं क्षेत्रफळ)

\begin{aligned} \\ &A\left(ABCDEFG\right)=25+9+0.5 \\ &A\left(ABCDEFG\right)=34.5\end{aligned}
\mathbf{\therefore } बहुभुजाकृती \mathbf{ABCDEFG} चं अंदाजे क्षेत्रफळ 24.5 चौरस सेमी आहे.

Go to top

इयत्ता 8 वी गणित पाठ्यपुस्तक: इथे क्लिक करा

इयत्ता 8 वी गणिताच्या संपूर्ण मार्गदर्शनासाठी खालील लिंक्सवर क्लिक करा: