इयत्ता 8 वी चौकोन रचना व प्रकार कोणते आहेत? : चार बाजू आणि चार कोन मिळून तयार होणाऱ्या भौमितिक आकृतीला चौकोन म्हणतात. चौरस, आयत, समभुज चौकोन, समांतरभुज चौकोन, समलंब चौकोन, पतंग हे चौकोनाचे प्रकार आहेत.

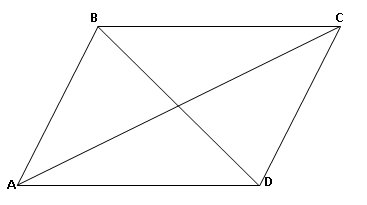
चौकोनाचे दहा घटक
कोणत्याही चौकोनाचे पुढील दहा घटक असतात (म्हणजेच खालील दहा घटक असलेल्या भौमितिक आकृतीला चौकोन म्हणतात.):
- 4 कोन (कोन A, कोन B, कोन C आणि कोन D)
- 4 बाजू (बाजू AB, बाजू BC, बाजू CD आणि बाजू DA)
- 2 कर्ण (कर्ण AC आणि कर्ण BD)
आता चौकोन रचना व प्रकार शिकण्याआधी आपण त्रिकोण रचनांची उजळणी करूयात; कारण चौकोन रचना शिकताना आपल्याला त्याचा उपयोग होणार आहे. आणि त्यासाठी आपण त्रिकोण रचनांची काही उदाहरणं बघुयात. खालील उदाहरणांमध्ये त्रिकोणांच्या काही घटकांची मापं दिलेली आहेत आणि त्याप्रमाणे त्रिकोणाच्या आकृत्या वहीत काढून बघायच्या आहेत.
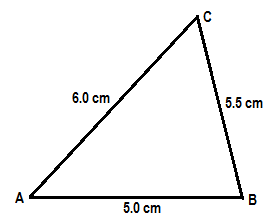
उदाहरण 1:
\triangle ABC: \ell\left(AB\right)=5 सेमी, \ell\left(BC\right)=5.5 सेमी, \ell\left(AC\right)=6 सेमी.
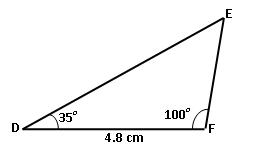
उदाहरण 2:
\triangle DEF: m\angle D=35^\circ, m\angle F=100^\circ,
\ell\left(DF\right)=4.8 सेमी.
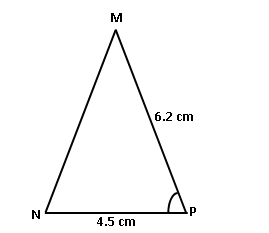
उदाहरण 3:
MNP:\ell\left(MP\right)= 6.2 सेमी, \left(NP\right)=4.5 सेमी, m\angle P=75^\circ
उदाहरण 4:
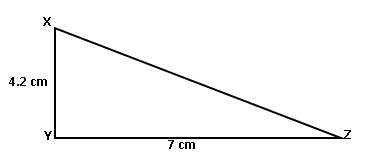
XYZ : m\angle Y=90°, \ell\left(XY\right)=4.2 सेमी, \ell\left(XZ\right)=7 सेमी
चौकोनाची रचना करायची असेल तर चौकोनाच्या वर दिलेल्या 10 पैकी 5 घटकांची माहिती असणं आवश्यक असतं. आणि महत्वाचं म्हणजे ह्या चौकोनाच्या रचना करण्यासाठी त्रिकोण रचनांचा आधार घ्यावा लागतो. आपण आता काही उदाहरणांच्या साह्याने हे समजावून घेऊ.
चौकोन रचना
1. चौकोनाच्या चार बाजू आणि एक कर्ण दिला असता चौकोन रचना करणे.
उदाहरण :
\Box PQRS असा काढा की,
\ell\left(PQ\right)=5.6 सेमी,
\ell\left(QR\right)=5 सेमी,
\ell\left(PS\right)=4.3 सेमी,
\ell\left(RS\right)=7 सेमी,
\ell\left(QS\right)=6.2 सेमी
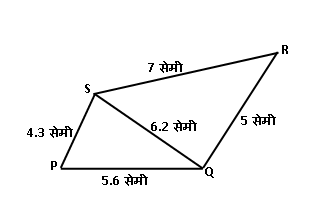
आता शेजारील आकृतीतील चौकोन \Box PQRS बघितला की तुमच्या सहज लक्षात येईल की ही चौकोन रचना दोन त्रिकोणांनी तयार झालेली आहे. \triangle PQS आणि \triangle SQR.
| महत्वाचं: याचा अर्थ असा की चौकोन रचनांचा आधार हा त्रिकोण रचना हाच असतो. |
2. चौकोनाच्या तीन बाजू आणि दोन कर्ण दिले असता चौकोन रचना करणे.
\Box WXYZ असा काढा की,
\ell\left(YZ\right)=4 सेमी,
\ell\left(ZX\right)=6 सेमी,
\ell\left(WX\right)=4.5 सेमी,
\ell\left(ZW\right)=5 सेमी,
\ell\left(YW\right)=6.5 सेमी.
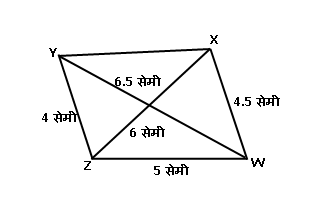
आता वर दिलेली रेषाखंडांची मापं बघितल्यावर तुमच्या लक्षात येईल की आपल्याला \triangle WXZ आणि \triangle WZY च्या सर्व बाजूंची मापं दिलेली आहेत. दिलेल्या मापांनुसार आपण हे दोन त्रिकोण काढले आणि बिंदू X आणि Y हे रेषाखंड XY ने जोडले की आपल्याला हवी असलेली \Box WXTZ ही चौकोन रचना मिळेल.
3. चौकोनाच्या लगतच्या दोन बाजू व कोणतेही तीन कोन दिले असता चौकोन रचना करणे.
\Box LEFT असा काढा की,
\ell\left(EL\right)=4.5 सेमी,
\ell\left(EF\right)=5.5 सेमी,
m\angle L=60^\circ,
m\angle E=100^\circ,
m\angle F=120^\circ
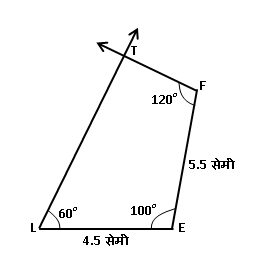
- ही चौकोन रचना तयार करताना प्रथम 4.5 सेमी लांबीचा रेख LE काढून घ्यायचा.
- त्यानंतर बिंदू L वर कोनमापक ठेऊन त्यावर 60 अंशाचा कोन घेऊन एक किरण काढायचा.
- त्याच प्रमाणे बिंदू E वर कोनमापक ठेऊन त्यावर 100 अंशाचा कोन घेऊन 5.5 सेमी लांबीचा रेख EF काढायचा.
- आता बिंदू F वर कोनमापक ठेऊन त्यावर 120 अंशाचा कोन घेऊन बिंदू F पासून एक किरण काढायचा.
- आता बिंदू L वर 60 अंशाचा कोन करणारा किरण आणि बिंदू F वर 120 अंशाचा कोन करणारा किरण, ज्या बिंदूत छेदतात, त्याला T नाव द्या.
अशा प्रकारे आपण \Box LEFT ही चौकोन रचना तयार करू शकतो.
4. चौकोनाच्या तीन बाजू आणि त्यांनी समाविष्ट केलेले कोन दिले असता चौकोन रचना करणे.
\Box PQRS असा काढा की,
\ell\left(QR\right)=5 सेमी,
\ell\left(RS\right)=6.2 सेमी,
\ell\left(SP\right)=4 सेमी,
m\angle R=62^\circ,
m\angle S=75^\circ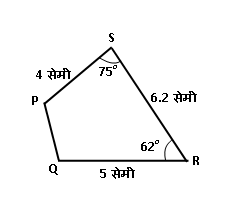
- ही चौकोन रचना तयार करताना प्रथम 5 सेमी लांबीचा रेख QR काढून घ्या.
- बिंदू R वर कोनमापक ठेऊन त्यावर 62 अंशाचा कोन घेऊन 6.2 सेमी लांबीचा रेख RS काढा.
- आता बिंदू S वर कोनमापक ठेऊन त्यावर 75 अंशाचा कोन घेऊन 4 सेमी लांबीचा रेख SP काढा.
- शेवटी बिंदू P आणि बिंदू Q ह्यांना जोडणारा रेख PQ काढून चौकोन पूर्ण करा.
अशा प्रकारे आपण \Box PQRS ही चौकोन रचना तयार करू शकतो.
चौकोन रचना उदाहरणे
उदाहरण 1:
\Box MORE मध्ये,
\ell\left(MO\right)=5.8 सेमी,
\ell\left(OR\right)=4.4 सेमी,
m\angle M=58^\circ,
m\angle O=105^\circ,
m\angle R=90^\circ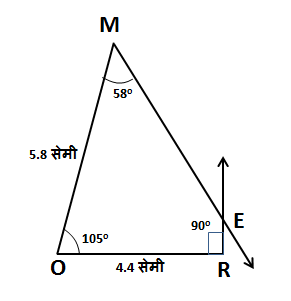
मित्रांनो, इथे आपल्याला दोन बाजू आणि तीन कोनांची मापं दिलेली आहेत. दिलेली मापं लक्षपूर्वक बघा, म्हणजे आकृतीची सुरुवात कुठून करता येईल, हे तुमच्या लक्षात येईल.
आपल्याला रेख OR चं माप 4.4 सेमी दिलेलं आहे. त्याचबरोबर \angle O आणि \angle R ची मापं देखील दिलेली असल्याने रेख OR काढून आपण ह्या आकृतीची सुरुवात करू शकतो.
- प्रथम 4.4 सेमी लांबीचा रेख OR काढून घ्या.
- आता बिंदू R वर कोनमापक ठेऊन त्यावर 90 अंशाचा कोन घेऊन एक किरण काढा.
- त्यानंतर बिंदू O वर कोनमापक ठेऊन त्यावर 105 अंशाचा कोन घेऊन 5.8 सेमी लांबीचा रेख OM काढा.
- आता बिंदू M वर कोनमापक ठेऊन त्यावर 58 अंशाचा कोन घेऊन एक किरण काढा.
- आता बिंदू R मधून निघालेला किरण आणि बिंदू M मधून निघालेला किरण ज्या बिंदूत छेदतात त्याला E नाव द्या.
- अशा प्रकारे आपल्याला \Box MORE ही चौकोन रचना तयार करता येते.
उदाहरण 2:
\Box DEFG असा काढा की,
\ell\left(DE\right)=4.5 सेमी,
\ell\left(EF\right)=6.5 सेमी,
\ell\left(DG\right)=5.5 सेमी,
\ell\left(DF\right)=7.2 सेमी,
\ell\left(EG\right)=7.8 सेमी.
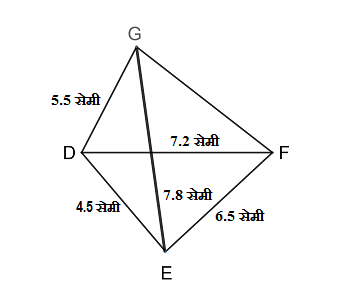
मित्रानो, ह्या उदाहरणात आपल्याला चौकोन रचनेच्या तीन बाजूंची आणि दोन कर्णांची मापं दिलेली आहेत. ही आकृती काढताना आपल्याला त्रिकोण रचना विचारात घ्यावी लागणार आहे.
- प्रथम 7.2 सेमी लांबीचा रेख DF काढून घ्या.
- 6.5 सेमी लांबीचा रेख EF काढण्यासाठी कंपास पेटीतील कंपासच्या साह्याने बिंदू F हे केंद्र घेऊन 6.5 सेमी त्रिज्येचे एक वर्तुळ काढा.
- 4.5 सेमी लांबीचा रेख ED काढण्यासाठी कंपास पेटीतील कंपासच्या साह्याने बिंदू D हे केंद्र घेऊन 4.5 सेमी त्रिज्येचे एक वर्तुळ काढा.
- आता वर काढलेली दोन वर्तुळं ज्या बिंदूत छेदतात, त्या बिंदूला E नाव द्या.
- बिंदू E आणि बिंदू D जोडण्यासाठी रेख DE काढा आणि बिंदू E आणि बिंदू F जोडण्यासाठी रेख EF काढा.
- अशा प्रकारे आपल्याला पहिला \triangle DEF मिळतो.
- 7.8 सेमी लांबीचा कर्ण काढण्यासाठी कंपास पेटीतील कंपासच्या साह्याने बिंदू E हे केंद्र घेऊन 7.8 सेमी त्रिज्येचे एक वर्तुळ काढा.
- 5.5 सेमी लांबीचा रेख DG काढण्यासाठी कंपास पेटीतील कंपासच्या साह्याने बिंदू D हे केंद्र घेऊन 5.5 सेमी त्रिज्येचे एक वर्तुळ काढा.
- आता वर काढलेली दोन वर्तुळं ज्या बिंदूत छेदतात, त्या बिंदूला G नाव द्या.
- बिंदू D आणि बिंदू G जोडण्यासाठी रेख DG काढा आणि बिंदू F आणि बिंदू G जोडण्यासाठी रेख FG काढा.
- अशा प्रकारे आपल्याला दुसरा \triangle DGF मिळतो.
- \triangle DEF आणि \triangle DGF मिळून आपल्याला \Box DEFG ही चौकोन रचना मिळते.
उदाहरण 3:
\Box ABCD मध्ये,
\ell\left(AB\right)=6.4 सेमी,
\ell\left(BC\right)=4.8 सेमी,
m\angle A=70^\circ,
m\angle B=50^\circ,
m\angle C=140^\circ.
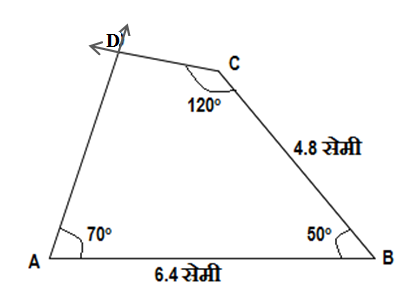
मित्रांनो, ह्या उदाहरणात आपल्याला चौकोन रचनेच्या दोन बाजू आणि तीन कोनांची मापं दिलेली आहेत.
- प्रथम 6.4 सेमी लांबीचा रेख AB काढून घ्या.
- बिंदू A वर कोनमापक ठेऊन त्यावर 70 अंशाचा कोन घेऊन एक किरण काढा.
- बिंदू B वर कोनमापक ठेऊन त्यावर 50 अंशाचा कोन घेऊन 4.8 सेमी लांबीचा रेख BC काढा.
- बिंदू C वर कोनमापक ठेऊन त्यावर 120 अंशाचा कोन घेऊन एक किरण काढा.
- आता बिंदू A मधून निघालेला किरण आणि बिंदू C मधून निघालेला किरण ज्या बिंदूत छेदतात त्याला D नाव द्या.
- अशा प्रकारे आपल्याला \Box ABCD ही चौकोन रचना तयार करता येते.
उदाहरण 4:
\Box LMNO काढा.
\ell\left(LM\right)=\ell\left(LO\right)=6 सेमी,
\ell\left(ON\right)=\ell\left(NM\right)=4.5 सेमी,
\ell\left(OM\right)=7.5 सेमी
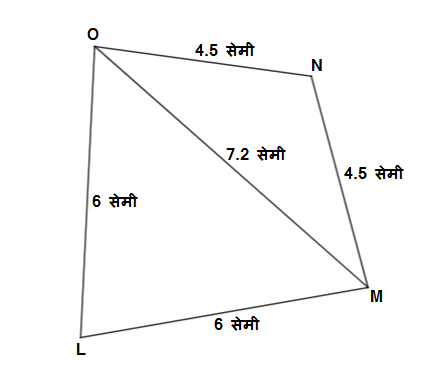
मित्रांनो, ह्या उदाहरणात आपल्याला चौकोन रचनेच्या चार बाजू आणि एका कर्णाची मापं दिलेली आहेत.
- प्रथम 7.2 सेमी लांबीचा कर्ण OM काढून घ्या.
- कंपास पेटीतील कंपासच्या साह्याने बिंदू O हे केंद्र घेऊन 6 सेमी त्रिज्येचे एक वर्तुळ काढा.
- कंपासच्या साह्याने बिंदू M हे केंद्र घेऊन 6 सेमी त्रिज्येचे एक वर्तुळ काढा.
- आता वरील 6 सेमी त्रिज्येच्या वर्तुळांच्या छेद बिंदूला L नाव द्या.
- आता बिंदू O आणि बिंदू L हे रेख OL ने जोडा.
- आता बिंदू O आणि बिंदू M हे रेख OM ने जोडा.
- आता कंपास पेटीतील कंपासच्या साह्याने बिंदू O हे केंद्र घेऊन 4.5 सेमी त्रिज्येचे एक वर्तुळ काढा.
- कंपास पेटीतील कंपासच्या साह्याने बिंदू M हे केंद्र घेऊन 6 सेमी त्रिज्येचे एक वर्तुळ काढा.
- आता वरील 4.5 सेमी त्रिज्येच्या वर्तुळांच्या छेद बिंदूला N नाव द्या.
- आता बिंदू O आणि बिंदू N हे रेख ON ने जोडा.
- आता बिंदू M आणि बिंदू N हे रेख MN ने जोडा.
- अशा प्रकारे आपल्याला \triangle MLO आणि \triangle MON मिळतात आणि ह्या दोन त्रिकोणांनी तयार झालेली \square LMNO ही चौकोन रचना मिळते.
चौकोन प्रकार
चौकोनाच्या बाजू आणि त्याचे कोन, ह्यांच्या मापात बदल केले की आपल्याला वेगवेगळे चौकोन प्रकार मिळतात. उदाहरणार्थ चौरस, आयत, समभुज चौकोन वगैरे. आता आपण हे वेगवेगळे चौकोन प्रकार बघुयात. हे चौकोन प्रकार शिकत असताना वर उल्लेख केलेले चौकोन रचनांचे 10 घटक पक्के लक्षात ठेवायचे. आणि हे देखील लक्षात ठेवायचं की ह्या 10 पैकी कोणतेही 5 घटक माहित असले की आपण ती चौकोन रचना रेखाटू शकतो. त्याचप्रमाणे चौकोन काढण्यासाठी 5 घटकांपैकी 2 लगतच्या बाजू माहित असाव्या लागतात. म्हणजेच दोन लगतच्या बाजू आणि तीन कोन माहित असतील तर चौकोन काढता येतो.
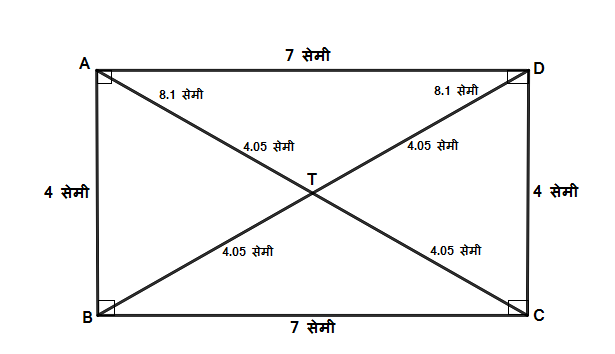
आयत किंवा काटकोन चौकोन
- चौकोन प्रकार आयताचे चारही कोन हे काटकोन किंवा 90 अंशाचे असतात. म्हणजेच शेजारील आकृतीत, m\angle DAB=m\angle ABC=
m\angle BCD=m\angle CDA=90^\circ - त्याचप्रमाणे आयताच्या समोरासमोरील दोन बाजू समान लांबीच्या असतात किंवा एकरूप असतात. म्हणजेच शेजारील आकृतीत, \ell\left(AB\right)=\ell\left(CD\right)=4 सेमी आणि \ell\left(BC\right)=\ell\left(AD\right)=7 सेमी.
- आयताचे दोन्ही कर्ण देखील समान लांबीचे किंवा एकरूप असतात. म्हणजेच शेजारील आकृतीत \ell\left(AC\right)=\ell\left(BD\right)=8.1 सेमी.
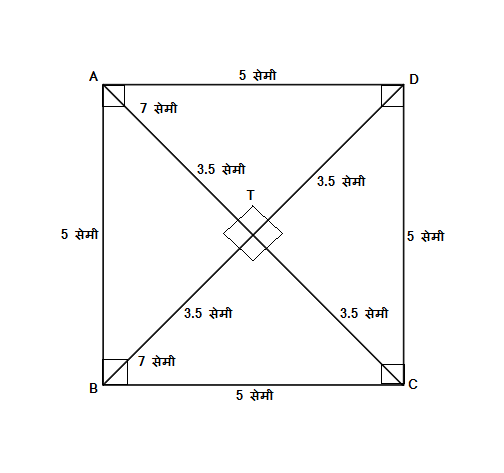
चौरस
चौकोन प्रकार चौरसाचे चारही कोन हे काटकोन किंवा 90 अंशाचे असतात. म्हणजेच शेजारील आकृतीत, m\angle DAB=m\angle ABC=
m\angle BCD=m\angle CDA=90^\circ
चौरसाच्या चारही बाजू समान लांबीच्या किंवा एकरूप असतात. म्हणजेच शेजारील आकृतीत, \ell\left(AB\right)=\ell\left(BC\right)=
\ell\left(CD\right)=\ell\left(DA\right)=5 सेमी.
चौरसाचे दोन्ही कर्ण देखील समान लांबीचे किंवा एकरूप असतात. म्हणजेच शेजारील आकृतीत \ell\left(AC\right)=\ell\left(BD\right)=7 सेमी.
चौरसाचे दोन्ही कर्ण एकमेकांना काटकोनात किंवा 90 अंशात छेदतात. म्हणजेच m\angle ATB=m\angle BTC=
m\angle CTD=m\angle DTA=90^\circ
चौरसाचे कर्ण एकमेकांना दुभागतात. दुभागतात म्हणजे दोन्ही कर्ण एकमेकांना त्यांच्या मध्य बिंदूत छेदतात तेंव्हा चार समान लांबीचे रेषाखंड तयार होतात. म्हणजेच शेजारील आकृतीत \ell\left(AT\right)=\ell\left(TC\right)=
\ell\left(BT\right)=\ell\left(TD\right)=3.5 सेमी.
चौरसाचे कर्ण चौरसाचे संमुख कोन दुभागतात. संमुख कोन दुभागतात म्हणजे चौरसाच्या बाजूंमुळे तयार झालेल्या 90 अंशांच्या कोनांना (\angle A,\angle B,\angle C आणि \angle D) 45 अंशाच्या दोन वेगवेगळ्या कोनांत विभागतात. म्हणजेच शेजारील आकृतीत;
1) m\angle BAD (90^\circ)=
m\angle DAT (45^\circ)+m\angle TAB (45^\circ)
2) m\angle ABC (90^\circ)=
m\angle ABT (45^\circ)+m\angle TBC (45^\circ)
3) m\angle BCD (90^\circ)=
m\angle BCT (45^\circ)+m\angle TCD (45^\circ)
4) m\angle CDA (90^\circ)=
m\angle CDT (45^\circ)+m\angle TDA (45^\circ)
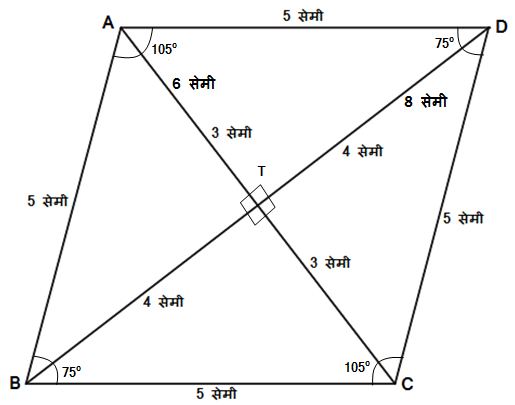
समभुज चौकोन
1) चौकोन प्रकार समभुज चौकोनाच्या चारही बाजू समान लांबीच्या किंवा एकरूप असतात. म्हणजेच शेजारील आकृतीत, \ell\left(AB\right)=\ell\left(BC\right)=
\ell\left(CD\right)=\ell\left(DA\right)=5 सेमी.
2) समभुज चौकोनाचे समोरासमोरील (संमुख) कोन समान अंशाचे किंवा एकरूप असतात. म्हणजेच शेजारील आकृतीत,
m\angle BAD=m\angle BCD=105^\circ
m\angle ABC=m\angle ADC=75^\circ
3) समभुज चौकोनाचे दोन्ही कर्ण एकमेकांना काटकोनात किंवा 90 अंशात छेदतात. म्हणजेच m\angle ATB=m\angle BTC=
m\angle CTD=m\angle DTA=90^\circ.
4) समभुज चौकोनाचे कर्ण एकमेकांना दुभागतात. दुभागतात म्हणजे दोन्ही कर्ण एकमेकांना त्यांच्या मध्य बिंदूत छेदतात. म्हणजेच शेजारील आकृतीत,
\ell\left(AT\right)=\ell\left(TC\right)=3 सेमी.
\ell\left(BT\right)=\ell\left(TD\right)=4 सेमी.
5) समभुज चौकोनाचे कर्ण समभुज चौकोनाचे समोरासमोरील (संमुख) कोन दुभागतात. संमुख कोन दुभागतात म्हणजे चौरसाच्या बाजूंमुळे तयार झालेल्या कोनांना दोन सामान कोनांत विभागतात. म्हणजेच शेजारील आकृतीत,
1) m\angle BAD (105^\circ)=
m\angle DAT (52.5^\circ)+m\angle TAB (52.5^\circ)
2) m\angle BCD (105^\circ)=
m\angle DCT (52.5^\circ)+m\angle TCB (52.5^\circ)
3) m\angle ABC (75^\circ)=
m\angle ABT (37.5^\circ)+m\angle TBC (37.5^\circ)
4) m\angle ADC (75^\circ)=
m\angle ADT (37.5^\circ)+m\angle TDC (37.5^\circ)
समांतरभुज चौकोन
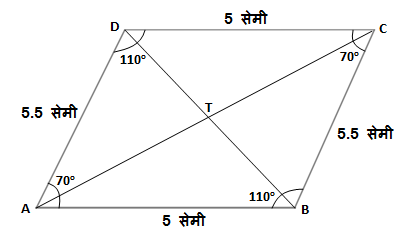
चौकोन प्रकार समांतरभुज चौकोनाच्या समोरासमोरील किंवा सन्मुख बाजू एकमेकांना समांतर असतात.
समांतर भुज चौकोन काढण्यासाठी,
1) ठराविक लांबीचा रेख AB काढून घ्या.
2) आता बिंदू A वर कोनमापक ठेऊन कोणताही एक कोन घेऊन (उदाहरणादाखल आपण 70 अंशाचा कोन घेऊयात) ठराविक लांबीचा रेख AD काढा.
3) वरील प्रमाणे आता बिंदू B वर कोनमापक ठेऊन बिंदू A वर ज्या मापाचा कोन घेतला आहे, त्याच मापाचा कोन घेऊन रेख BC काढा. इथे लक्षात घ्या की,
m\angle ABC=180^\circ-m\angle DAB
\therefore m\angle ABC=110^\circ
4) आता बिंदू C आणि बिंदू D ला जोडणारा रेख CD काढून चौकोन ABCD पूर्ण करा.
5) समांतरभुज चौकोनाच्या समोरासमोरील बाजू (संमुख बाजू) समान लांबीच्या, म्हणजेच एकरूप असतात.
\therefore \ell\left(AD\right) \parallel \ell\left(BC\right)=5.5 सेमी आणि \ell\left(AB\right) \parallel \ell\left(CD\right)=5 सेमी.
6) समांतरभुज चौकोनाचे समोरासमोरील कोन (संमुख कोन) समान मापाचे, म्हणजेच एकरूप असतात.
\therefore m\angle DAB=m\angle BCD=70^\circ आणि m\angle ADC=m\angle ABC=110^\circ
7) तसेच समांतरभुज चौकोनाच्या लगतच्या कोनांच्या जोड्या परस्पर पूरक असतात.
\begin{aligned} \\ \therefore\; & m\angle+m\angle B=180^\circ, \\ & m\angle B+m\angle C=180^\circ, \\ & m\angle C+m\angle D=180^\circ,\\ & m\angle D+m\angle A=180^\circ\end{aligned}
8) समांतर भुज चौकोनाचे कर्ण एकमेकांना त्यांच्या मध्यबिंदूत छेदतात किंवा दुभागतात.
समलंब चौकोन
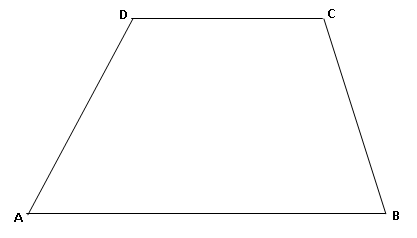
1) चौकोन प्रकार समलंब चौकोनात समोरासमोरील (संमुख) बाजूंच्या दोन जोड्यांपैकी एक जोडी समांतर असते.
उदाहरणार्थ शेजारील आकृतीत बाजू AB आणि बाजू CD ह्या दोन बाजू एकमेकींना समांतर आहेत.
2) त्याच प्रमाणे बाजू AD आणि बाजू BC ह्या छेदिका असून त्यांच्यामुळे तयार होणारे आंतर कोन हे एकमेकांना पूरक असतात.
म्हणजेच, m\angle CDA+m\angle DAB=180^\circ आणि m\angle ABC+m\angle BCD=180^\circ
(छेदिका म्हणजे काय?: जेंव्हा एखादी रेषा दिलेल्या दोन रेषांना वेगवेगळ्या दोन बिंदूत छेदत असेल तर त्या रेषेला त्या दोन रेषांची छेदिका म्हणतात.)
पतंग
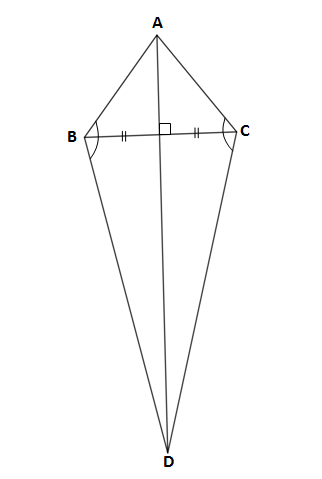
चौकोन प्रकार पतंगचा महत्वाचा गुणधर्म म्हणजे ह्याचा एक कर्ण दुसऱ्या कर्णाचा लंबदुभाजक असतो.
शेजारच्या आकृतीत, कर्ण AD हा कर्ण BC चा लंबदुभाजक आहे. म्हणजेच कर्ण AD हा कर्ण BC ला त्याच्या मध्यबिंदूत काटकोनात (90 अंशात) छेदत आहे.
1) पतंगाच्या संमुख कोनांची एक जोडी एकरूप असते. शेजारील आकृतीत,
m\angle ABD=m\angle ACD
2) त्याच प्रमाणे पतंगाच्या लगतच्या बाजूंच्या दोन जोड्या एकरूप असतात. शेजारील आकृतीत,
\ell\left(AB\right)=\ell\left(AC\right) आणि \ell\left(BD\right)=\ell\left(CD\right)
उदाहरणे
उदाहरण 1:
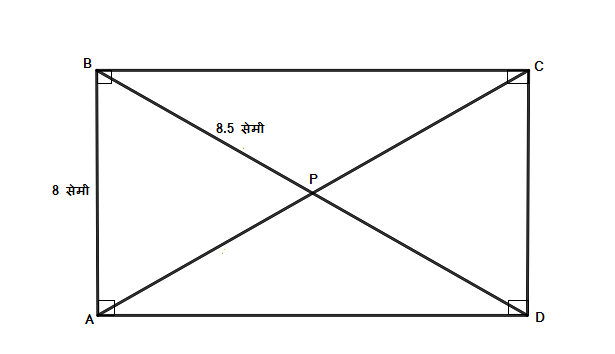
चौकोन प्रकार आयत ABCD च्या कर्णांचा छेदनबिंदू P आहे.
1) \ell\left(AB\right)=8 सेमी तर \ell\left(CD\right)= किती?
2)\ell\left(BP\right)=8.5 सेमी तर \ell\left(BD\right) आणि \ell\left(BC\right) काढा.
उत्तर:
आयताच्या समोरासमोरील (संमुख) बाजू एकरूप असतात. (म्हणजेच त्या बाजूंची लांबी समान असते).
1) \mathbf{\therefore \ell\left(AB\right)=\ell\left(CD\right)=8} सेमी.
2) आयताचे कर्ण एकमेकांना दुभागतात, म्हणजेच आयताचे कर्ण जेंव्हा एकमेकांना त्यांच्या मध्य बिंदूत छेदतात, तेंव्हा त्या कर्णांचे दोन सामान भाग होतात.
\therefore \ell\left(BD\right)=\ell\left(BP\right)+\ell\left(PD\right) आणि \ell\left(BP\right)=\ell\left(PD\right)
\therefore \ell\left(BD\right)=2 \times \ell\left(BP\right)
\therefore \ell\left(BD\right)=2 \times \left(8.5\right)
\mathbf{\therefore \ell\left(BD\right)=17} सेमी.
आता आपल्याला बाजू DC आणि बाजू BD ची लांबी माहित असल्याने आपण पायथागोरस प्रमेय वापरून बाजू BC ची लांबी काढू,
\triangle BCD हा काटकोन त्रिकोण आहे. पायथॅगोरस प्रमेयाप्रमाणे,
\begin{aligned} \\ & \therefore \ell\left(BD\right)^2=\ell\left(BC\right)^2+\ell\left(CD\right)^2 \\ & \therefore \ell\left(17\right)^2=\ell\left(BC\right)^2+\left(8\right)^2 \\ & \therefore 289=\ell\left(BC\right)^2+64 \\ & \therefore \ell\left(BC\right)^2=289 -64 \\ & \therefore \ell\left(BC\right)^2=225 \\ & \therefore \ell\left(BC\right)=\sqrt{225} \\ & \mathbf{\therefore \ell\left(BC\right)=15}\end{aligned}
उदाहरण 2:
बाजू 6 सेमी असलेल्या चौरसाच्या कर्णाची लांबी काढा.
उत्तर:
शेजारील आकृतीत प्रत्येक बाजूची लांबी ६ सेमी असलेला चौरस दिलेला आहे आणि रेख PR हा त्याचा कर्ण आहे.
कर्ण PR ची लांबी काढण्यासाठी आपल्याला \triangle PQR हा काटकोन त्रिकोण विचारात घ्यावा लागणार आहे आणि त्यासाठी आपल्याला पायथॅगोरसचे प्रमेय वापरावे लागणार आहे.
पायथागोरसच्या प्रमेयाप्रमाणे
\begin{aligned} \\ & \ell\left(PR\right)^2=\ell\left(PQ\right)^2+\ell\left(QR\right)^2 \\ & \therefore \ell\left(PR\right)^2=\left(6\right)^2+\left(6\right)^2 \\ & \therefore \ell\left(PR\right)^2=36+36 \\ & \therefore \ell\left(PR\right)^2=72 \\ & \therefore \mathbf{\ell\left(PR\right)=\sqrt{72}}\end{aligned}
चौकोन प्रकार चौरसाचे दोनही कर्ण एकरूप असल्याने, \mathbf{\ell\left(QS\right)=\ell\left(PR\right)=\sqrt{72}}
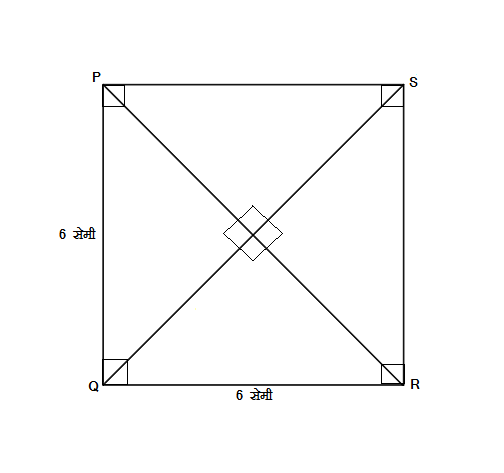
उदाहरण 3:
\square BEST ह्या समभुज चौकोनाचे कर्ण एकमेकांना बिंदू A मध्ये छेदतात.
(i) जर m\angle BTS=110^\circ, तर m\angle TBS काढा.
(ii)जर \ell\left(TE\right)=24, \ell\left(BS\right)= 70, तर \ell\left(TS\right)= किती?
उत्तर:
चौकोन प्रकार समभुज चौकोनाचे समोरासमोरचे (संमुख) कोन हे समान मापाचे किंवा एकरूप असतात.
\therefore m\angle BTS=m\angle BES=110^\circ
\therefore m\angle EBT=m\angle EST=?
आपल्याला माहित आहे की चौकोनाच्या चारही कोनांच्या मापांची बेरीज 360^\circ असते.
\begin{aligned} \\ & \therefore m\angle BTS+m\angle TSE+ \\ &\phantom{xx}m\angle SEB+m\angle EBT=360^\circ \\ & \therefore 110^\circ+m\angle TSE+110^\circ+m\angle EBT=360^\circ \\ & \therefore 220^\circ+m\angle TSE+m\angle EBT=360^\circ \\ & \therefore m\angle TSE+m\angle EBT=360^\circ-220^\circ \\ & \therefore 2\times m\angle EBT=140^\circ \\ & \therefore m\angle EBT=\frac{140^\circ}{2} \\ & \therefore m\angle EBT=70^\circ\end{aligned}
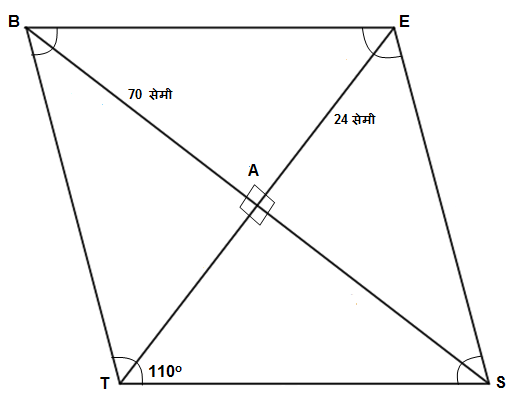
| पण आपल्याला माहित आहे की चौकोन प्रकार समभुज चौकोनाचे कर्ण त्याच्या संमुख कोनांना दुभागतात, म्हणजे कोनांची दोन सामान कोनांमध्ये विभागणी करतात. \\ m\angle TBS=\frac{1}{2}\times m\angle EBT \\ m\angle TBS=\frac{1}{2}\times 70^\circ \\ \mathbf{m\angle TBS=35^\circ} \ell\left(TE\right)=24, \ell\left(BS\right)=70, पण आपल्याला माहित आहे की समभुज चौकोनाचे कर्ण एकमेकांना त्यांच्या मध्यबिंदूत काटकोनात, म्हणजे 90 अंशात छेदतात. |
| \\ \therefore \ell\left(TA\right)=\frac{1}{2}\times \ell\left(TE\right) \\ \therefore \ell\left(TA\right)=\frac{1}{2}\times {24} \\ \therefore \ell\left(TA\right)=12 | \\ \therefore \ell\left(AS\right)=\frac{1}{2}\times \ell\left(BS\right) \\ \therefore \ell\left(AS\right)=\frac{1}{2}\times {70} \\ \therefore \ell\left(AS\right)=35 |
| चौकोन प्रकार समभुज चौकोनाचे कर्ण एकमेकांना काटकोनात दुभागतात, \therefore \triangle TAS हा काटकोन त्रिकोण असून m\angle TAS=90^\circ आणि बाजू TS हा कर्ण आहे. पायथॅगोरस प्रमेय वापरून, \\ \ell\left(TS\right)^2=\ell\left(TA\right)^2+\ell\left(AS\right)^2 \\ \therefore \ell\left(TS\right)^2=\left(12\right)^2+\left(35\right)^2 \\ \therefore \ell\left(TS\right)^2=144+1225 \\ \therefore \ell\left(TS\right)^2=1369 \\ \therefore \ell\left(TS\right)=\sqrt{1369} \\ \mathbf{\therefore \ell\left(TS\right)=37} |
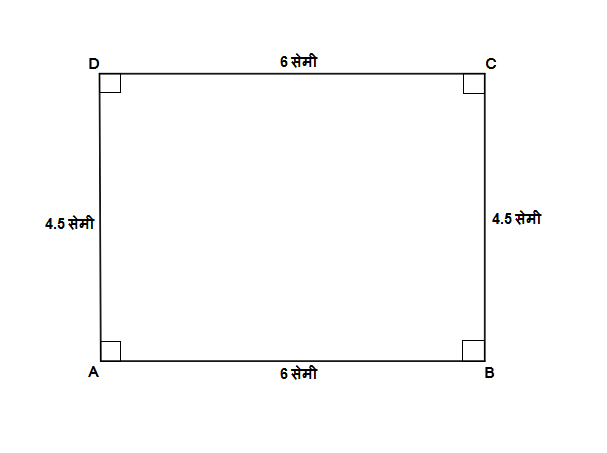
उदाहरण 4:
\ell\left(AB\right)=6.0 सेमी आणि \ell\left(BC\right)=4.5 सेमी असा चौकोन प्रकार आयत ABCD काढा.
उत्तर:
1) \square ABCD हा आयत काढताना प्रथम 6 सेमी लांबीचा रेख AB काढून घ्या.
2) आता बिंदू A वर कोनमापक ठेऊन 90 अंशाचा कोन घेऊन 4.5 सेमी लांबीचा रेख AD काढा.
3) बिंदू B वर कोनमापक ठेऊन 90 अंशाचा कोन घेऊन 4.5 सेमी लांबीचा रेख BC काढा.
4) आता बिंदू C आणि बिंदू D ला जोडण्यासाठी रेख CD काढा आणि आयत \square ABCD पूर्ण करा.
5) रेख CD ची लांबी 6 सेमी आहे आणि m\angle ADC=m\angle BCD=90^\circ आहे ह्याची खात्री करून घ्या.
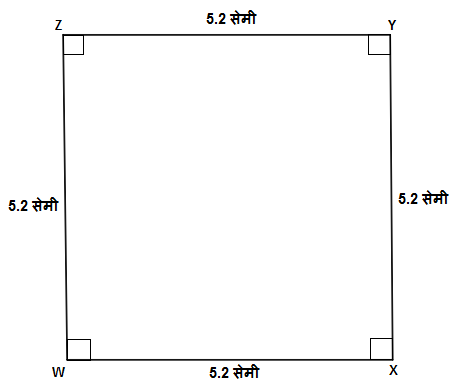
उदाहरण 5:
बाजू 5.2 सेमी असलेला चौकोन प्रकार चौरस WXYZ काढा.
उत्तर:
1) \square WXYZ हा चौरस काढताना प्रथम 5.2 सेमी लांबीचा रेख WX काढून घ्या.
2) आता बिंदू W वर कोनमापक ठेऊन 90 अंशाचा कोन घेऊन 5.2 सेमी लांबीचा रेख WZ काढा.
3) बिंदू X वर कोनमापक ठेऊन 90 अंशाचा कोन घेऊन 5.2 सेमी लांबीचा रेख XY काढा.
4) आता बिंदू Y आणि बिंदू Z ला जोडण्यासाठी रेख YZ काढा आणि चौरस \square WXYZ पूर्ण करा.
5) रेख YZ ची लांबी 6 सेमी आहे आणि m\angle WZY=m\angle XYZ=90^\circ आहे ह्याची खात्री करून घ्या.
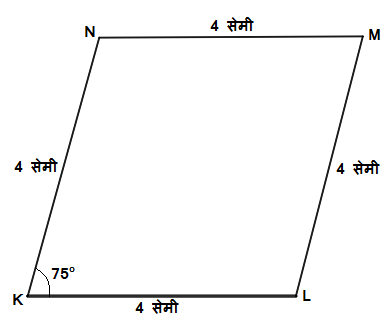
उदाहरण 6:
बाजू 4 सेमी आणि m\angle K=75^\circ असा चौकोन प्रकार समभुज चौकोन \square KLMN काढा.
उत्तर:
1) \square KLMN हा समभुज चौकोन काढताना प्रथम 4 सेमी लांबीचा रेख KL काढून घ्या.
2) आता बिंदू K वर कोनमापक ठेऊन 75 अंशाचा कोन घेऊन 4 सेमी लांबीचा रेख KN काढा.
3) बिंदू L वर कोनमापक ठेऊन 75 अंशाचा कोन घेऊन 4 सेमी लांबीचा रेख LM काढा.
4) आता बिंदू M आणि बिंदू N ला जोडण्यासाठी रेख MN काढा आणि चौरस \square KLMN पूर्ण करा.
5) रेख MN ची लांबी 4 सेमी आहे, ह्याची खात्री करून घ्या.
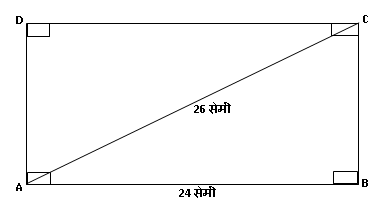
उदाहरण 7:
एका आयताचा कर्ण 26 सेमी असून त्याची एक बाजू 24 सेमी आहे, तर त्याची दुसरी बाजू काढा.
उत्तर:
1) आपल्याला माहित आहे की आयताचे चारही कोन हे काटकोन (90 अंशाचे) असतात.
2) इथे आयत \square ABCD चा कर्ण रेख AC आहे आणि तो आयताला \triangle ABC आणि \triangle ADC अशा दोन “काटकोन त्रिकोणांत” विभागतो आहे.
3) आपल्याला कर्ण AC आणि बाजू AB ची लांबी माहित आहे आणि बाजू BC ची लांबी काढायची आहे.
4) बाजू BC ची लांबी काढण्यासाठी आपल्याला \triangle ABC हा काटकोन त्रिकोण विचारात घ्यावा लागणार आहे. \triangle ABC हा काटकोन त्रिकोण असल्याने आपण पायथॅगोरसचं प्रमेय वापरून बाजू BC ची लांबी काढू शकतो.
\begin{aligned} \\& \therefore \ell\left(AC\right)^2=\ell\left(AB\right)^2+\ell\left(BC\right)^2 \\ & \therefore \left(26\right)^2=\left(24\right)^2+\ell\left(BC\right)^2 \\ & \therefore \left(676\right)=\left(576\right)+\ell\left(BC\right)^2 \\ & \therefore \ell\left(BC\right)^2=\left(676\right)-\left(576\right) \\ & \therefore \ell\left(BC\right)^2=100 \\ & \therefore \ell\left(BC\right)=\sqrt {100} \\ & \therefore \ell\left(BC\right)=10\end{aligned}
\therefore आयताच्या दुसऱ्या बाजूची लांबी 10 सेमी आहे.
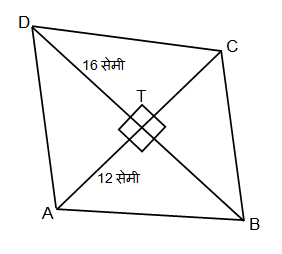
उदाहरण 8:
समभुज चौकोन \square ABCD च्या कर्णाची लांबी 16 सेमी व 12 सेमी आहेत, तर त्या समभुज चौकोनाची बाजू व परिमिती.
उत्तर:
समभुज चौकोनाचे कर्ण एकमेकांना दुभागतात, म्हणजेच समभुज चौकोनाचे कर्ण जेंव्हा एकमेकांना छेदतात, तेंव्हा त्यांची दोन समान भागांत विभागणी होते.
\begin{aligned} \\ \therefore \ell\left(AT\right)=\ell\left(TC\right)&=\;\frac{1}{2}\times \ell\left(AC\right) \\ &=\;\frac{1}{2}\times 12 \\ &=\;6\end{aligned}
\begin{aligned} \\ \therefore \ell\left(BT\right)=\ell\left(TD\right)&=\;\frac{1}{2}\times \ell\left(BD\right) \\ &=\;\frac{1}{2}\times 16 \\ &=\;8\end{aligned}
आता आपण पायथॅगोरसचं प्रमेय वापरून \square ABCD च्या एका बाजूची, म्हणजे बाजू AD ची लांबी काढू,
\begin{aligned} \\ & \therefore \ell\left(AD\right)^2=\ell\left(AT\right)^2+\ell\left(DT\right)^2 \\ & \therefore \left(AD\right)^2=\left(6\right)^2+\ell\left(8\right)^2 \\ & \therefore \left(AD\right)=\left(36\right)+\ell\left(64\right)^2 \\ & \therefore \ell\left(AD\right)^2=100 \\ & \therefore \ell\left(AD\right)=\sqrt {100} \\ & \therefore \ell\left(AD\right)=10 \\ & \therefore \ell\left(AD\right)=\ell\left(AB\right)= \\ & \ell\left(BC\right)=\ell\left(CD\right)=10\end{aligned}
समभुज चौकोनाची परिमिती,
P = 4 x (समभुज चौकोनाची कोणतीही एक बाजू)
\begin{aligned} \\ \therefore P&=4\times\ell\left(AD\right) \\ &=4\times 10 \\ &=40\end{aligned}
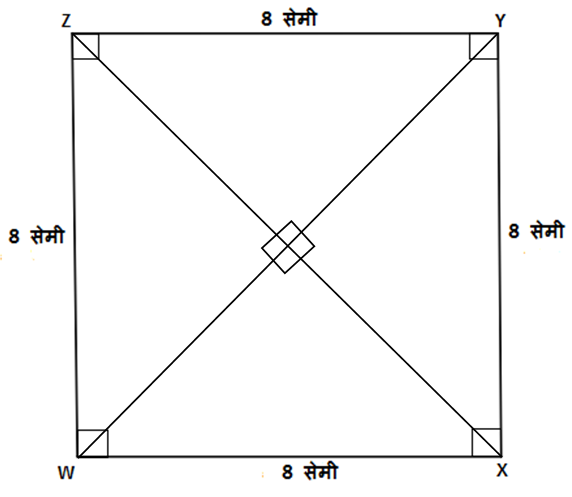
उदाहरण 9:
बाजू 8 सेमी असलेल्या चौरसाच्या कर्णाची लांबी काढा.
उत्तर:
1) \square WXYZ हा प्रत्येकी 8 सेमी लांबी असलेल्या बाजूंनी तयार झालेला चौरस आहे.
2) रेख WY आणि रेख XZ हे ह्या चौरसाचे दोन कर्ण आहेत.
3) आपल्याला माहित आहे की चौरसाचे कर्ण एकमेकांच्या मध्यबिंदूत काटकोनात छेदतात. ह्या आकृतीत बिंदू T हा चौरसाच्या दोन कर्णांचा छेदबिंदू आहे.
4) चौरस \square WXYZ ची लांबी काढण्यासाठी आपल्याला \triangle XYZ विचारात घ्यावा लागणार आहे आणि पायथॅगोरसचे प्रमेय वापरून कर्ण XZ ची लांबी काढावी लागणार आहे.
\begin{aligned} \\& \therefore \ell\left(XZ\right)^2=\ell\left(XY\right)^2+\ell\left(YZ\right)^2 \\ & \therefore \ell\left(XZ\right)^2=\left(8\right)^2+\left(8\right)^2 \\ & \therefore \ell\left(XZ\right)^2=\left(64\right)+\left(64\right) \\ & \therefore \ell\left(XZ\right)^2=128 \\ & \mathbf{\therefore \ell\left(XZ\right)=\sqrt {128}}\end{aligned}
उदाहरण 10:
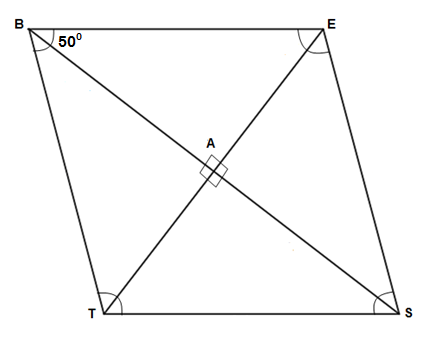
एका समभुज चौकोनाच्या एका कोनाचे माप 50^\circ आहे, तर त्याच्या इतर तीन कोनांची मापे काढा.
उत्तर:
1) आपल्याला माहित आहे की समभुज चौकोनाचे समोरासमोरील (संमुख) कोन समान मापाचे असतात.
\mathbf{\therefore m\angle EBT=m\angle TSE=50^\circ}
2) त्याच प्रमाणे आपल्याला हे ही माहित आहे की समभुज चौकोनाच्या चारही कोनांच्या मापांची बेरीज 360 अंश असते.
\begin{aligned} \\ & \therefore m\angle EBT+m\angle TSE+ \\ & \phantom{xx}m\angle BTS+m\angle BES=360^\circ \\ & \therefore 50^\circ+50^\circ+ \\ & \phantom{xx}m\angle BTS+m\angle BES=360^\circ \\ & \therefore 100^\circ+m\angle BTS+m\angle BES=360^\circ \\ & \therefore m\angle BTS+m\angle BES=360^\circ-100^\circ \\ & \therefore m\angle BTS+m\angle BES=260^\circ \\ & \therefore 2\times m\angle BTS=260^\circ\;\left(\because m\angle BTS=m\angle BES \right) \\ & \therefore m\angle BTS=\frac{260^\circ}{2} \\ & \mathbf{\therefore m\angle BTS=130^\circ} \\ & \mathbf{\therefore m\angle BES=130^\circ}\end{aligned}
उदाहरण 11:
एका समांतरभुज चौकोनाच्या लगतच्या कोनांची मापे \left(5x - 7\right)^\circ आणि \left(4x + 25\right)^\circ आहेत. तर त्या कोनांची मापे काढा.
उत्तर:
एका कोनाचे माप: \left(5x - 7\right)^\circ
दुसऱ्या कोनाचे माप: \left(4x + 25\right)^\circ
हे गणित सोडवताना इथे आपल्याला x ची किंमत आधी काढून घ्यावी लागणार आहे आणि नंतर ती x ची किंमत वरील समीकरणात वापरून आपल्याला कोनांची मापं मिळतील. चला तर मग आधी आपण x ची किंमत काढून घेऊ.
आपल्याला माहित आहे की समांतर भुज चौकोनाचे लगतचे कोन परस्परांना पूरक असतात, म्हणजे त्यांच्या मापांची बेरीज 180 अंश असते.
\begin{aligned} \\ & \therefore \left(5x - 7\right)+\left(4x + 25\right)=180^\circ \\ & \therefore 9x+18=180^\circ \\ & \therefore 9x=180-18 \\ & \therefore 9x=162 \\ & \therefore x=\frac{162}{9} \\ & \therefore x=18\end{aligned}
आता ही x ची किंमत वरील समीकरणात वापरून आपल्याला कोनांची मापं मिळतील,
\begin{aligned} \\ \therefore \left(5x-7\right)^\circ&=\left(5\times 18-7\right)^\circ \\ &=\left(90-7\right)^\circ \\ &=\mathbf{83^\circ}\end{aligned}
\begin{aligned} \\ \therefore \left(4x+25\right)^\circ&=\left(4\times 18+25\right)^\circ \\ &=\left(72+25\right)^\circ \\ &=\mathbf{97^\circ}\end{aligned}
उदाहरण 12:
सोबतच्या आकृतीत \square ABCD समांतरभुज चौकोन आहे. त्याच्या कर्णांचा छेदनबिंदू T आहे. आकृतीच्या आधारे पुढील प्रश्नांची उत्तरं लिहा
1) जर \ell\left(CD\right)=5.4 सेमी, तर \ell\left(AB\right)= किती ?
उत्तर: समांतरभुज चौकोनाच्या समोरासमोरील (संमुख) बाजू एकरूप असतात.
\therefore \ell\left(CD\right)=\ell\left(AB\right)=5.4 सेमी.
2) जर \ell\left(TC\right)=3.5 सेमी, तर \ell\left(AC\right)= किती ?
उत्तर: समांतरभुज चौकोनाचे कर्ण एकमेकांना त्यांच्या मध्यबिंदूत छेदतात (दुभागतात).
\begin{aligned} \\ & \therefore \ell\left(AC\right)=2\times \ell\left(TC\right) \\ & \therefore \ell\left(AC\right)=2\times \left(3.5\right) \\ & \therefore \ell\left(AC\right)=7\end{aligned}
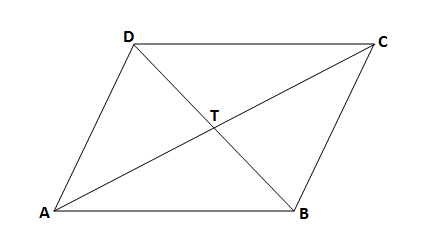
3) m\angle ABC=118^\circ, तर m\angle ADC= किती?
उत्तर: समांतरभुज चौकोनाचे समोरासमोरील कोन (संमुख) एकरूप असतात,
\therefore m\angle ABC=m\angle ADC=118^\circ
4) m\angle CBD=72^\circ तर m\angle BDA= किती?
उत्तर: \angle CBD आणि \angle BDA हे व्युत्क्रम कोन असल्याने एकरूप आहेत.
\therefore m\angle CBD=m\angle BDA=72^\circ.
उदाहरण 13:
\square CWPR च्या क्रमागत कोनांच्या मापांचे गुणोत्तर 7ः9ः3ः5 आहे, तर त्या चौकोनाच्या कोनांची
मापे काढा आणि चौकोनाचा प्रकार ओळखा.
उत्तर:
कोनांच्या मापांचे गुणोत्तर 7ः9ः3ः5 आहे.
आपल्याला माहित आहे की चौकोनाच्या चारही कोनांच्या मापांची बेरीज 360 अंश असते.
\\ \therefore m\angle A=m\angle B= \\<br>\phantom{x}m\angle C=m\angle D=360^\circ.
दिलेल्या प्रमाणाप्रमाणे आपण ह्या चारही कोनांची मापं खालील प्रमाणे मानू,
m\angle A=7x, m\angle B=9x,
m\angle C=3x, m\angle D=5x.
आधी आपण x ची किंमत काढून घेऊ आणि मग वर दिलेल्या कोणाच्या मापात ती किंमत वापरून आपल्याला कोनांची खरी मापं कळतील.
\begin{aligned} \\ &\therefore m\angle A=m\angle B= \\ &\phantom{x} m\angle C=m\angle D=360^\circ \\ &\therefore 7x+9x+3x+5x=360^\circ \\ &\therefore 24x=360^\circ \\ &\therefore x=\frac{360^\circ}{24} \\ &\therefore x=15 \\ \end{aligned}
आता आपण x=15 ही किंमत वापरून कोनांची मापं काढूयात,
\begin{aligned} & m\angle A=7x=7\times 15=105^\circ \\ & m\angle B=9x=9\times 15=135^\circ \\ & m\angle C=3x=3\times 15=45^\circ \\ & m\angle D=3x=5\times 15=75^\circ\end{aligned}
आता ह्या चौकोनाच्या प्रकार ओळखण्यासाठी आपण खालील काही गोष्टींची पडताळणी करून पाहू,
1)\begin{aligned} \\ & m\angle A+m\angle D=105^\circ+75^\circ=180^\circ \\ & \therefore \ell\left(AB\right)\parallel\ell\left(CD\right)\end{aligned}
म्हणजे बाजू AB आणि बाजू CD समांतर आहेत.
2) m\angle A+m\angle B=105^\circ+135^\circ=240^\circ\ne180^\circ
म्हणजे बाजू AD आणि बाजू BC समांतर नाहीत.
\mathbf{\square ABCD} च्या संमुख बाजूंची एकच जोडी समांतर असल्याने हा चौकोन प्रकार “समलंब चौकोन” आहे.
उदाहरण 14:
एका समांतरभुज चौकोनाच्या संमुख कोनांची मापे \left(3x-2\right)^\circ आणि \left(50 - x\right)^\circ आहेत, तर चौकोनाच्या प्रत्येक कोनाचे माप काढा.
उत्तर:
इथे समुख कोनांची (समोरासमोरील कोनांची) मापं दिलेली आहेत: \left(3x-2\right)^\circ आणि \left(50 - x\right)^\circ
आपल्याला माहित आहे की समांतरभुज चौकोनाचे संमुख कोन सारख्या मापाचे, म्हणजेच एकरूप असतात,
\begin{aligned} \\ & \therefore \left(3x-2\right)^\circ=\left(50 - x\right)^\circ \\ & \therefore \left(3x+x\right)^\circ=\left(50+2\right) \\ & \therefore 4x=52 \\ & \therefore x=\frac{52}{4} \\ & \therefore x=13\end{aligned}
आता वरील x ची किंमत दिलेल्या कोणाच्या मापांच्या समीकरणात वापरून आपल्याला कोनांची खरी मापं मिळतील.
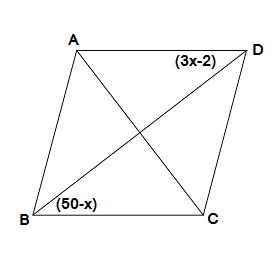
\begin{aligned} \\ & \therefore m\angle ADC=\left(3x-2\right) \\ & \therefore m\angle ADC=\left(3\times 13\right)-2 \\ & \therefore m\angle ADC=\left(39-2\right) \\ & \mathbf{\therefore m\angle ADC=37^\circ}\end{aligned}
आणि
\begin{aligned} \\ & \therefore m\angle ABC=\left(50-x\right) \\ & \therefore m\angle ABC=\left(50-13\right) \\ & \mathbf{\therefore m\angle ABC=37}^\circ\end{aligned}
चौकोन प्रकार समांतरभुज चौकोनाच्या संगत कोनांच्या मापांची बेरीज 180 अंश असते.
\begin{aligned} \\ & \therefore m\angle BAD+m\angle ADC=180^\circ \\ & \therefore m\angle BAD+37^\circ=180^\circ \\ & \therefore m\angle BAD=180^\circ-37^\circ \\ & \mathbf{\therefore m\angle BAD=143}^\circ\end{aligned}
समांतर भुज चौकोनाचे संमुख कोन सारख्या मापाचे, म्हणजेच एकरूप असतात,
\mathbf{m\angle BAD=m\angle BCD=143^\circ}
उदाहरण 15:
(1) जर \ell\left(WZ\right)=4.5 सेमी तर \ell\left(XY\right)=?
(2) जर \ell\left(YZ\right)=8.2 सेमी तर \ell\left(XW\right)=?
(3) जर \ell\left(OX\right)=2.5 सेमी तर \ell\left(OZ\right)=?
(4) जर \ell\left(WO\right)=3.3 सेमी तर \ell\left(WY\right)=?
(5) जर m\angle WZY=120^\circ तर m\angle WXY=? आणि m\angle XWZ=?
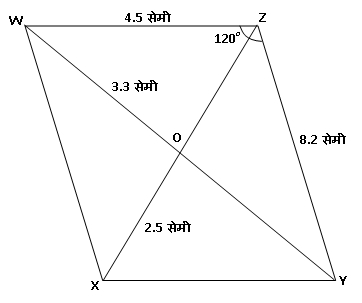
उत्तर:
आपल्याला माहित आहे की समांतरभुज चौकोनाच्या समोरासमोरील (संमुख ) बाजू ह्या समान लांबीच्या, म्हणजेच एकरूप असतात.
(1) \therefore \ell\left(XY\right)=\ell\left(WZ\right)=4.5 सेमी.
(2) \ell\left(XW\right)=\ell\left(YZ\right)=8.2 सेमी.
समांतरभुज चौकोनाचे कर्ण एकमेकांना त्यांच्या मध्य बिंदूत छेदतात (दुभागतात).
(3) \therefore \ell\left(OZ\right)=\ell\left(OX\right)=2.5 सेमी.
(4) \ell\left(WY\right)=2\times \ell\left(WO\right)=2\times3.3=6.6 सेमी.
समांतरभुज चौकोनाचे समोरासमोरील कोन समान मापाचे किंवा एकरूप असतात.
(5) m\angle WXY=m\angle WZY=120^\circ
समांतरभुज चौकोनाच्या संगत कोनांची बेरीज 180 अंश असते.
\begin{aligned} \\ & m\angle XWZ+m\angle WZY=180^\circ \\ & m\angle XWZ+120^\circ=180^\circ \\ & m\angle XWZ=180^\circ-120^\circ \\ & m\angle XWZ=60^\circ\end{aligned}
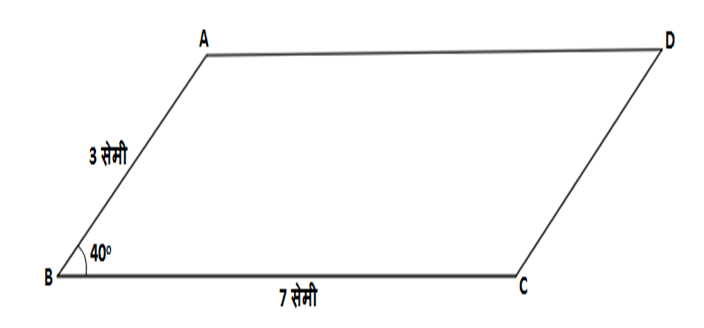
उदाहरण 16:
\square ABCD हा समांतरभुज चौकोन असा काढा की \ell\left(BC\right)=7 सेमी, m\angle ABC=40^\circ,<br>\ell\left(AB\right)=3 सेमी.
उत्तर:
(1) \square ABCD काढताना, प्रथम 7 सेमी लांबी रेखचा BC काढून घ्या.
(2) आता बिंदू B वर कोनमापक ठेऊन 40 अंशाचा कोन घेऊन 3 सेमी लांबीचा रेख AB काढा.
(3) रेख AB ला समांतर 3 सेमी लांबीचा रेख CD काढा.
(4) बिंदू A आणि बिंदू D ला जोडणारा रेख AD काढून \square ABCD पूर्ण करा.
(5) \square ABCD मधल्या खालील गोष्टी पडताळून बघा,
\begin{aligned} \\ & (i)\; \ell\left(AD\right)=\ell\left(BC\right) \\ & (ii)\; \ell\left(AB\right)=\ell\left(CD\right) \\ & (iii)\; m\angle BAD=m\angle BCD \\ & (iv)\; m\angle ABC=m\angle ADC \\ & (v)\; m\angle BAD+m\angle ABC=180^\circ \\ & (vii)\; m\angle ABC+m\angle BCD=180^\circ \\ & (vi)\; m\angle BCD+m\angle CDA=180^\circ \\ & (viii)\; m\angle CDA+m\angle BAD=180^\circ\end{aligned}
उदाहरण 17:
एका चौकोनाच्या चार क्रमागत कोनांचे प्रमाण 1:2:3:4 आहे, तर तो कोणत्या प्रकाराचा चौकोन असेल ? त्या चौकोनाच्या प्रत्येक कोनाचे माप काढा. कारण लिहा.
उत्तर:
कोनांच्या मापांचे प्रमाण 1:2:3:4 आहे.
आपल्याला माहित आहे की चौकोनाच्या चारही कोनांच्या मापांची बेरीज 360 अंश असते.
\therefore m\angle A=m\angle B=m\angle C=m\angle D=360^\circ.
दिलेल्या प्रमाणाप्रमाणे आपण ह्या चारही कोनांची मापं खालील प्रमाणे मानू,
m\angle A=1x, m\angle B=2x, m\angle C=3x, m\angle D=4x.
आधी आपण x ची किंमत काढून घेऊ आणि मग वर दिलेल्या कोणाच्या मापात ती किंमत वापरून आपल्याला कोनांची खरी मापं कळतील.
\begin{aligned} \\ & \therefore m\angle A=m\angle B=m\angle C=m\angle D=360^\circ \\ & \therefore 1x+2x+3x+4x=360^\circ \\ & \therefore 10x=360^\circ \\ & \therefore x=\frac{360^\circ}{24} \\ & \therefore x=36\end{aligned}
आता आपण x=36 ही किंमत वापरून कोनांची मापं काढूयात,
\begin{aligned} & m\angle A=1x=1\times 36=36^\circ \\ & m\angle B=2x=2\times 36=72^\circ \\ & m\angle C=3x=3\times 36=108^\circ \\ & m\angle D=4x=4\times 36=144 ^\circ \\ \end{aligned}
आता ह्या चौकोनाच्या प्रकार ओळखण्यासाठी आपण खालील काही गोष्टींची पडताळणी करून पाहू,
1)\begin{aligned} \\ & m\angle A+m\angle D=36^\circ+144^\circ=180^\circ \\ & \therefore \ell\left(AB\right)\parallel\ell\left(CD\right)\end{aligned}
म्हणजे बाजू AB आणि बाजू CD समांतर आहेत.
2) m\angle A+m\angle B=36^\circ+72^\circ=108^\circ\ne180^\circ
म्हणजे बाजू AD आणि बाजू BC समांतर नाहीत.
\mathbf{\square ABCD} च्या संमुख बाजूंची एकच जोडी समांतर असल्याने हा चौकोन प्रकार “समलंब चौकोन” आहे.
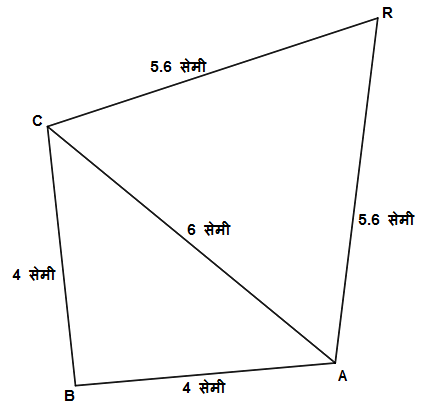
उदाहरण 18:
\square BARC असा काढा की \ell\left(BA\right)=\ell\left(BC\right)=4.2 सेमी, \ell\left(AC\right)=6.0 सेमी,
\ell\left(AR\right)=\ell\left(CR\right)=5.6 सेमी.
उत्तर:
1) प्रथम 6 सेमी लांबीचा रेख AC काढून घ्या.
2) 4 सेमी लांबीचा रेख AB काढण्यासाठी कंपास पेटीतील कंपासच्या साह्याने बिंदू A हे केंद्र घेऊन 4 सेमी त्रिज्येचे एक वर्तुळ काढा.
3) आता 4 सेमी लांबीचा रेख BC काढण्यासाठी कंपास पेटीतील कंपासच्या साह्याने बिंदू C हे केंद्र घेऊन 4 सेमी त्रिज्येचे एक वर्तुळ काढा.
5) आता वर काढलेली दोन वर्तुळं ज्या बिंदूत छेदतात, त्या बिंदूला B नाव द्या.
6) बिंदू A आणि बिंदू B जोडण्यासाठी रेख AB काढा आणि बिंदू B आणि बिंदू C जोडण्यासाठी रेख BC काढा.
7) अशा प्रकारे आपल्याला पहिला \triangle ABC मिळतो.8) 5.6 सेमी लांबीचा रेख AR काढण्यासाठी कंपास पेटीतील कंपासच्या साह्याने बिंदू A हे केंद्र घेऊन 5.6 सेमी त्रिज्येचे एक वर्तुळ काढा.
9) आता 5.6 सेमी लांबीचा रेख CR काढण्यासाठी कंपास पेटीतील कंपासच्या साह्याने बिंदू C हे केंद्र घेऊन 5.6 सेमी त्रिज्येचे एक वर्तुळ काढा.
10) आता वर काढलेली दोन वर्तुळं ज्या बिंदूत छेदतात, त्या बिंदूला R नाव द्या.
11) बिंदू A आणि बिंदू R जोडण्यासाठी रेख AR काढा आणि बिंदू C आणि बिंदू R जोडण्यासाठी रेख CR काढा.
12) अशा प्रकारे आपल्याला दुसरा \triangle ARC मिळतो.
13) \triangle ABC आणि \triangle ARC मिळून \square BARC तयार होतो.
उदाहरण 19:
\square PQRS असा काढा की \ell\left(PQ\right)=3.5 सेमी, \ell\left(QR\right)=5.6 सेमी, \ell\left(RS\right)=3.5 सेमी,
m\angle Q=110^\circ, m\angle R=70^\circ.
\square PQRS समांतरभुज आहे ही माहिती दिल्यास वरीलपैकी कोणती माहिती देणे आवश्यक नाही ते लिहा.
उत्तर:
\square PQRS हा चौकोन समांतरभुज चौकोन आहे, हे दिलेलं असेल तर m\angle Q=110^\circ, m\angle R=70^\circ ही माहिती दिलेली नसेल तरी चालेल, कारण समांतरभुज चौकोनाच्या संगत किंवा लगतच्या कोनांच्या मापांची बेरीज 180 अंश असतेच; त्यामुळे संगत किंवा लगतच्या कोनांच्या मापांची वेगळी माहिती देण्याची गरज नाही.
इयत्ता 8 वीचे पाठयपुस्तक: इथे क्लिक करा
